当前位置:网站首页>[leetcode] 96 and 95 (how to calculate all legal BST)
[leetcode] 96 and 95 (how to calculate all legal BST)
2022-07-04 12:46:00 【Learn a little every day】
How to calculate all legal BST
I wrote two articles before BST Algorithm related ⽂ Chapter , Chapter one About the middle order traversal pair BST The significance of , Second articles Yes BST Basic operation .
Ben ⽂ Say two questions step by step , Describe how to calculate all legal BST.
96. Different binary search trees
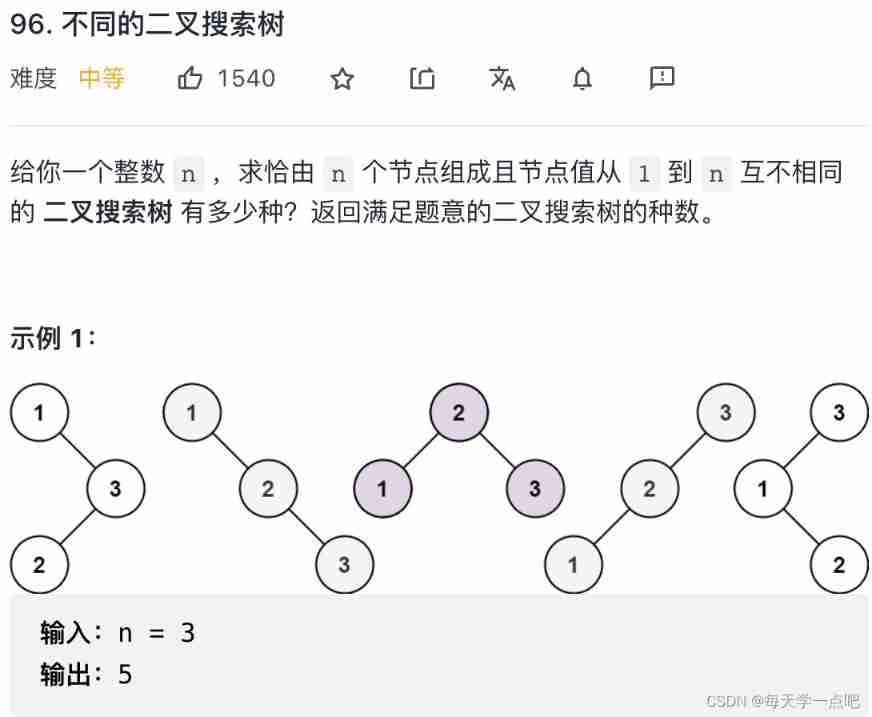
solution : recursive
This is an authentic problem of exhaustion , So what method can correctly enumerate the legal BST How about the number of ?
For interval [1,2,…,n], We calculate each number in turn as the root node , Then sum it up . For example, for n=5, Fixed number 3 As root node , Under this premise, there can be several different BST Well ?
Fix 3 Root node , according to BST characteristic , Its left subtree is a node [1,2] The combination of , The right subtree node is [4,5] The combination of , The product of the combination number of the left subtree and the combination number of the right subtree is 3 As the root node BST Number , be equal to 4.
Abstracted as a recursive process is , For any interval , Calculating the BST Number , Is a pair of BST The sum of the numbers . For any number root node , Its BST The number is , Left interval BST Number ( Combinatorial number ) Multiply by the right interval BST Number ( Combinatorial number ).
There are many repeating subproblems in recursive process , You can use memos ( In the code mamo Array ) To solve .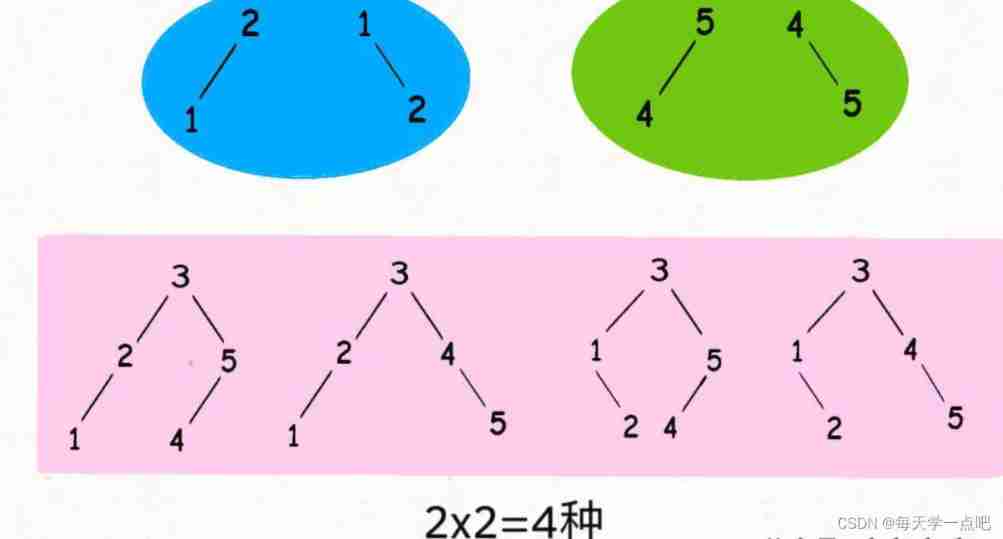
class Solution:
def numTrees(self, n: int) -> int:
mamo = [[0]*n for _ in range(n)]
# Calculate the closed interval [lo, hi] Composed of BST Number
def count(lo, hi):
nonlocal mamo
if lo >= hi:
return 1
# Check the memo
if mamo[lo][hi] != 0:
return mamo[lo][hi]
res = 0
for i in range(lo, hi+1):
# i As the root node root
left = count(lo, i-1)
right = count(i+1, hi)
# The product of the combination number of left and right subtrees is BST Total of
res += left*right
# Store memos
mamo[lo][hi] = res
return res
# Calculate the closed interval [1, n] Composed of BST Number
return count(0, n-1)
95. Different binary search trees 2
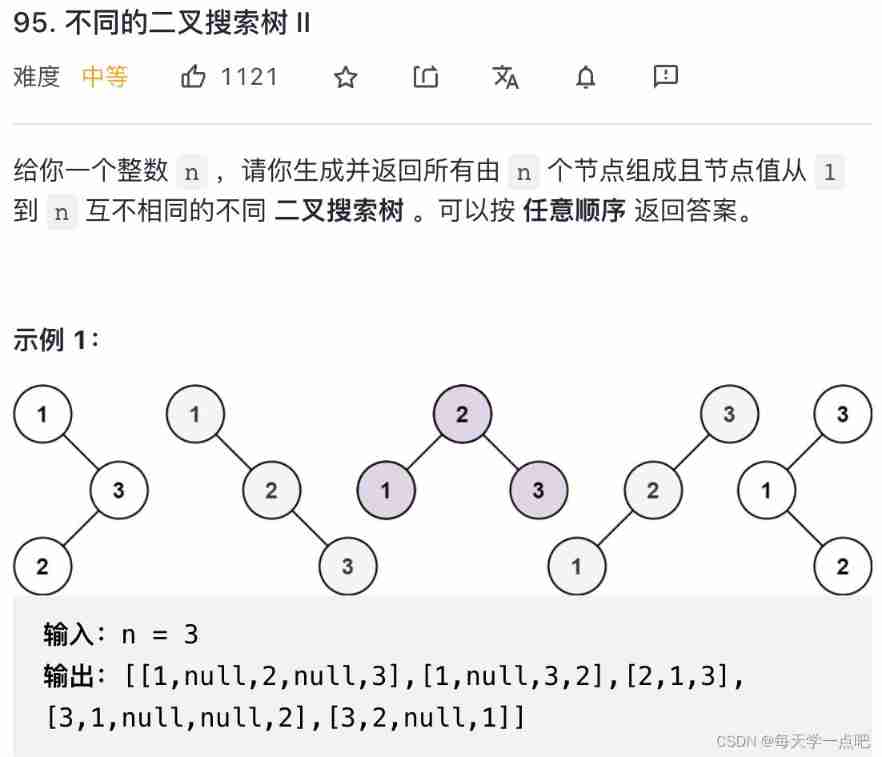
solution : recursive
Consistent with the above question , The original problem is decomposed into subproblems with left and right intervals , Recursively solve the original problem according to the return result of the subproblem . The specific steps are as follows :
- For a given interval , Exhausting root All possible nodes .
- Recursively construct all the legal properties of the left and right subtrees BST.
- to root The node enumerates the combination of all left and right subtrees . Return as result .
class Solution:
def generateTrees(self, n: int) -> List[TreeNode]:
# Memo operation
mamo = [[None]*(n+1) for _ in range(n+1)]
# Tectonic closed interval [lo, hi] Composed of BST
def count(lo, hi):
if lo > hi:
return [None]
if lo == hi:
return [TreeNode(lo)]
if mamo[lo][hi]:
return mamo[lo][hi]
result = []
# 1、 Exhausting root All possible nodes
for i in range(lo, hi+1):
# 2、 Recursively construct all the legal properties of the left and right subtrees BST.
l_result = count(lo, i-1)
r_result = count(i+1, hi)
# 3、 to root The node enumerates the combination of all left and right subtrees .
for left in l_result:
for right in r_result:
# i As root node root Value
root = TreeNode(i)
root.left = left
root.right = right
result.append(root)
mamo[lo][hi] = result
return result
return count(1, n)
边栏推荐
- Can Console. Clear be used to only clear a line instead of whole console?
- IIS error, unable to start debugging on the webserver
- IPv6 experiment
- Translation D29 (with AC code POJ 27:mode of sequence)
- It's hard to hear C language? Why don't you take a look at this (V) pointer
- Clion configuration of opencv
- Bottom Logic -- Mind Map
- LVS load balancing cluster deployment - Dr direct routing mode
- Googgle guava ImmutableCollections
- Vit (vision transformer) principle and code elaboration
猜你喜欢
ArcGIS uses grid processing tools for image clipping

Fly tutorial 02 advanced functions of elevatedbutton (tutorial includes source code) (tutorial includes source code)
Servlet learning notes

Leetcode day 17

0x15 string
Flet教程之 按钮控件 ElevatedButton入门(教程含源码)
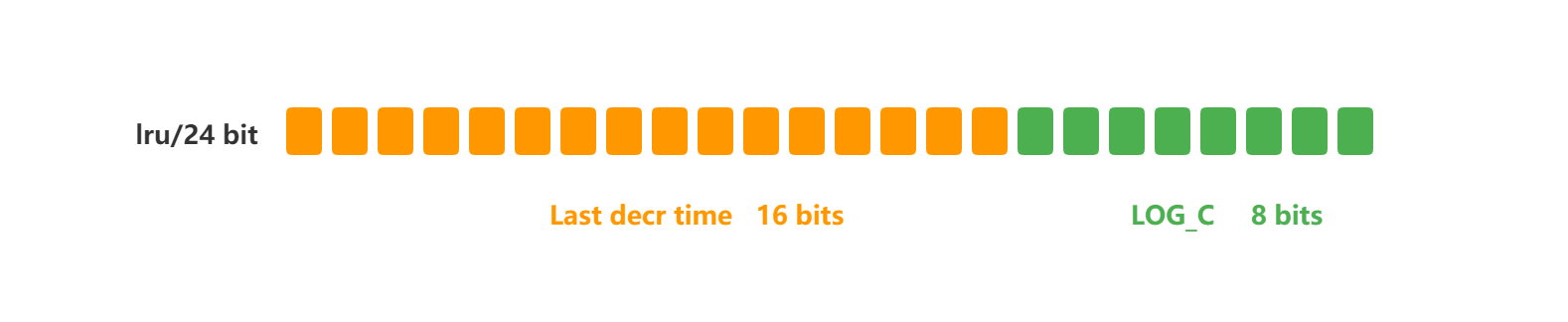
面试官:Redis 过期删除策略和内存淘汰策略有什么区别?
SAP ui5 date type sap ui. model. type. Analysis of the display format of date
Transformer principle and code elaboration (tensorflow)

When synchronized encounters this thing, there is a big hole, pay attention!
随机推荐
Azure solution: how can third-party tools call azure blob storage to store data?
Googgle guava ImmutableCollections
LVS load balancing cluster deployment - Dr direct routing mode
Article download address
ArgMiner:一个用于对论点挖掘数据集进行处理、增强、训练和推理的 PyTorch 的包
Mongodb vs mysql, which is more efficient
Leetcode day 17
Practice of retro SOAP Protocol
Data communication and network: ch13 Ethernet
游戏启动后提示安装HMS Core,点击取消,未再次提示安装HMS Core(初始化失败返回907135003)
IPv6 experiment
Lvs+kept highly available cluster
[ES6] template string: `string`, a new symbol in es2015
16. Memory usage and segmentation
When to use pointers in go?
How to use "bottom logic" to see the cards in the world?
Jetson TX2配置Tensorflow、Pytorch等常用库
Complementary knowledge of auto encoder
[Android kotlin] lambda return statement and anonymous function
Flet教程之 按钮控件 ElevatedButton入门(教程含源码)