[data clustering] section 3 of Chapter 4: DBSCAN performance analysis, advantages and disadvantages, and parameter selection methods

7、 ... and ： Performance analysis

DBSCAN The algorithm retrieves all points in its neighborhood for each point in the data set , The time complexity is $O(n^2)$. But in low latitude space , If the $k$-$d$ Trees 、$R$ Trees and other structures , It can effectively retrieve all points within a given distance of a specific point , Its time complexity can be reduced to $O(nlogn)$

8、 ... and ： Advantages and disadvantages

（1） advantage

①： It can be done to Clustering dense data sets of arbitrary shape

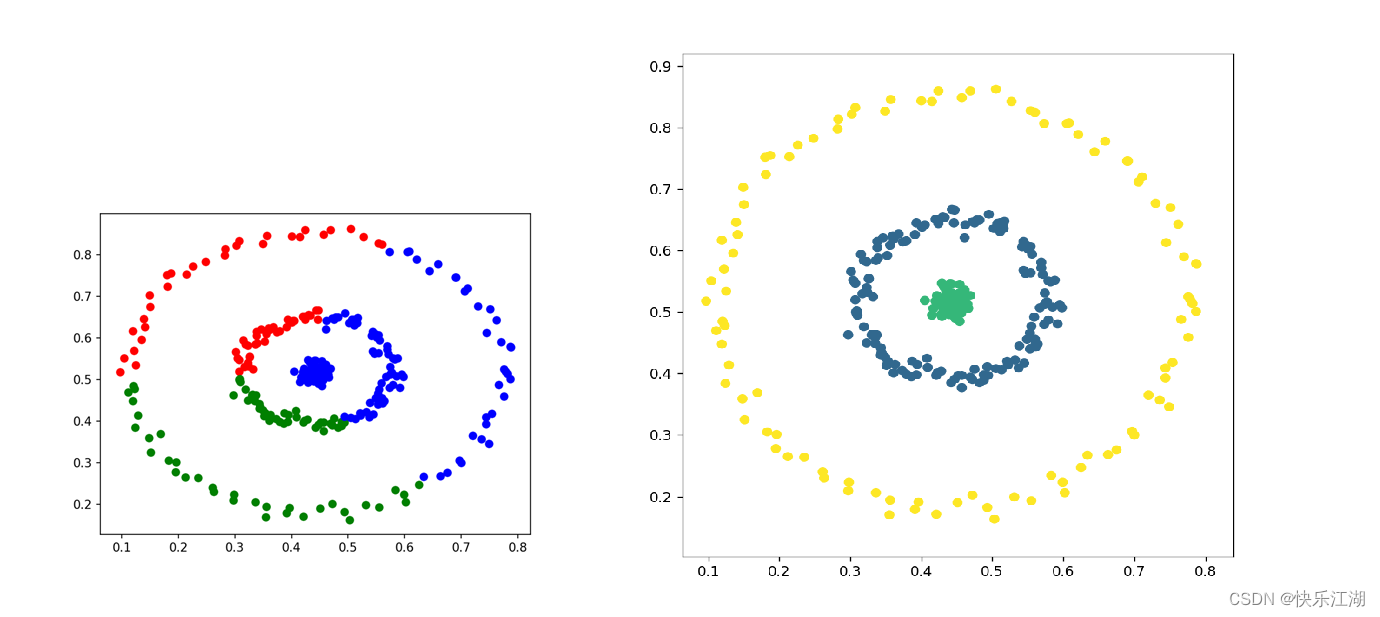
②： We can find outliers while clustering , Insensitive to outliers in the dataset

③： There is no need to specify the number of clusters , And the results of many experiments are often the same

（2） shortcoming

①： If the density of the sample set is not uniform 、 When the distance between clusters is very different , The clustering quality is poor , Use DBSCAN Clustering is generally not suitable for

②： Tuning parameters are compared to K-Means More complicated , Different parameter combinations have a great impact on the clustering effect

③： Due to the traditional European distance Can't handle high latitude data well , Therefore, it is difficult to give a good solution to the definition of distance

④：DBSCAN The algorithm is suitable for dealing with the density of different clusters Relatively uniform The situation of , When When the density of different clusters changes greatly There will be some problems

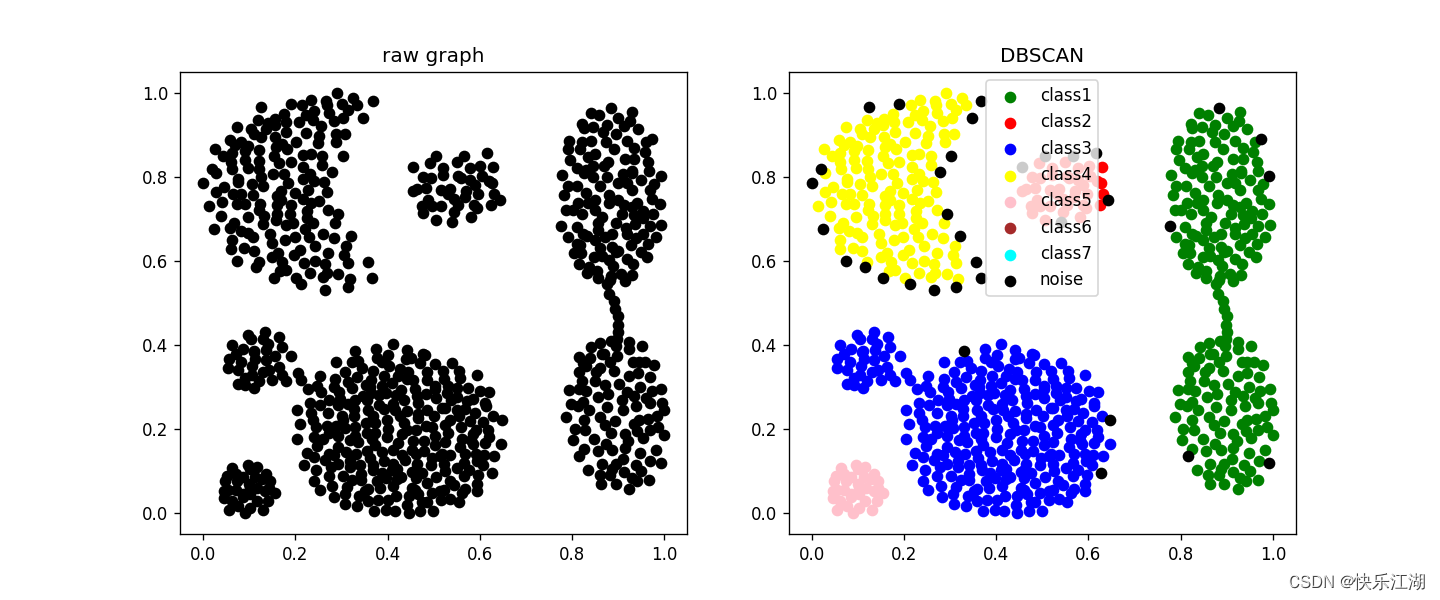
• From the clustering rendering shown in the previous section , You may find this algorithm It is easy to mark some data points as noise
  

Nine ： Parameter selection

（1） Basic principles of modifying parameters

When visualization is complete , We can fine tune the parameters according to the clustering results

• min_pts： General choice dimension +1 Or dimension ×2 that will do
• eps： If you share Less classes , Then put eps Turn it down ; If you share There are more classes , Then put eps Turn it up

（2） according to K-dist Figure adjustment parameters

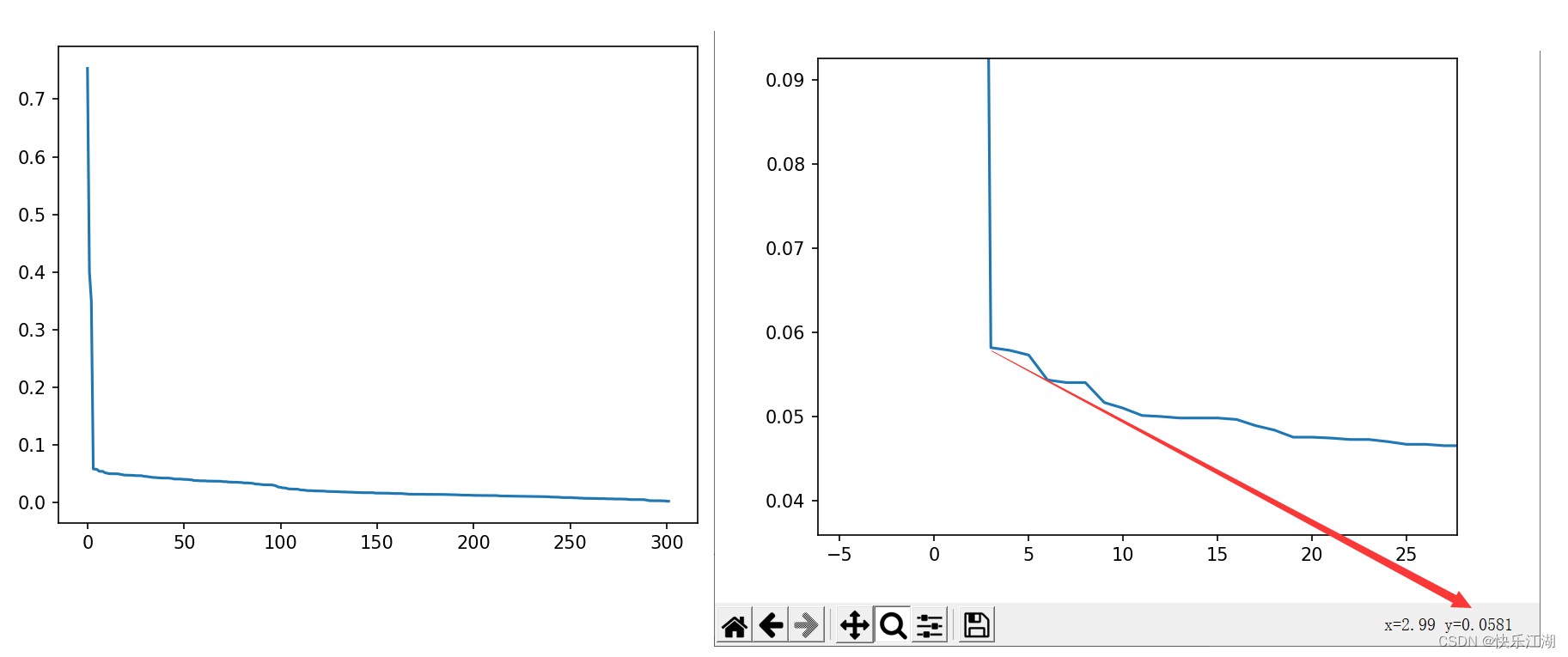
Parameter adjustment method ： You can use observation The first $k$ Nearest neighbor distance （$k$ distance ） Method to determine parameters . For a point in the cluster , If $k$ No more than the number of samples in the cluster , be $k$ The distance will be very small , then For noise ,$k$ The distance will be great . therefore ： For any positive integer $k$, Calculate all data points $k$ distance , Then sort it incrementally , Then draw $k$- Distance map , At the inflection point, it is appropriate eps, Because boundary points or noise points are often encountered at the inflection point

• $k$ distance ： For a given data set $P$=$\{p_1,p_2,...,p_n\}$, Calculation point $p(i)$ To dataset $D$ Subset $S$ The distance between all points in the , The distances are sorted from small to large , be $d(k)$ It's called $k$ distance

The specific steps are as follows

1. determine K value , Usually take 2* dimension -1
2. draw K-dist chart
3. Inflection point position （ The most volatile place ） by eps（ You can take multiple inflection points to try ）
4. min_pts Can take K+1

k = 3  #  take 2*2-1
k_dist = select_minpts(train_data, k)  # K Distance map 
k_dist.sort()  #  Sort （ Default ascending order ）
plt.plot(np.arange(k_dist.shape[0]), k_dist[::-1])  #  Draw from large to small 
plt.show()


def select_minpts(data_set, k):
    k_dist = []
    for i in range(data_set.shape[0]):
        dist =  (((data_set[i] - data_set)**2).sum(axis=1)**0.5)
        dist.sort()
        k_dist.append(dist[k])
    return np.array(k_dist)

as follows eps It is suggested that 0.0581

Ten ：DBSCAN Algorithm and K-Means Algorithm comparison

	DBSCAN	K-Means
Algorithmic thought	be based on density	be based on Divide
Required parameters	Eps and MinPts	Number of clusters $k$
Data requirement	Make no assumptions about the data distribution	Suppose that all clusters come from a spherical Gaussian distribution
High dimensional data	Not suitable for	fit （ sparse ）
formalization	You can't	It can be formalized as an optimization problem that minimizes the sum of squares of errors from each point to the center of mass
stability	Stable	unstable
Time complexity	$O(n^2)$	$O(n)$