当前位置:网站首页>[set theory] Cartesian product (concept of Cartesian product | examples of Cartesian product | properties of Cartesian product | non commutativity | non associativity | distribution law | ordered pair
[set theory] Cartesian product (concept of Cartesian product | examples of Cartesian product | properties of Cartesian product | non commutativity | non associativity | distribution law | ordered pair
2022-07-03 04:17:00 【Programmer community】
List of articles
- One 、 Cartesian product
- Two 、 Examples of Cartesian products
- 3、 ... and 、 Cartesian product property
- Four 、 n Vicat product
- 5、 ... and 、 n The number of Vicat's products
- 6、 ... and 、 n Vicat product property
Front blog : 【 Set theory 】 Ordered pair ( Ordered pair | Ordered triples | Orderly n Yuan Zu )
One 、 Cartesian product
Cartesian product :
A
,
B
A , B
A,B It's two sets , from
A
A
A The element in the set is the first element , from
B
B
B The element in the set is the second element , A set of ordered pairs that meet the above conditions , Called a set
A
A
A And
B
B
B The Cartesian product of ;
Write it down as :
A
×
B
A \times B
A×B
Symbolize :
A
×
B
=
{
<
x
,
y
>
∣
x
∈
A
∧
y
∈
B
}
A \times B = \{ <x, y> | x \in A \land y \in B \}
A×B={ <x,y>∣x∈A∧y∈B}
aggregate
A
A
A And aggregate
B
B
B Of Cartesian product It's a New collection , This new set is a Ordered pair set ;
Two 、 Examples of Cartesian products
aggregate
A
=
{
∅
,
a
}
A = \{ \varnothing , a \}
A={ ∅,a} , aggregate
B
=
{
1
,
2
,
3
}
B = \{ 1, 2, 3 \}
B={ 1,2,3}
A
×
B
=
{
<
∅
,
1
>
,
<
∅
,
2
>
,
<
∅
,
3
>
,
<
a
,
1
>
,
<
a
,
2
>
,
<
a
,
3
>
}
A \times B = \{ <\varnothing , 1> , <\varnothing , 2>, <\varnothing , 3>, <a, 1> , <a, 2> , <a , 3> \}
A×B={ <∅,1>,<∅,2>,<∅,3>,<a,1>,<a,2>,<a,3>}
Each ordered pair The first element comes from
A
A
A aggregate , The second element comes from
B
B
B aggregate ;
B
×
A
=
{
<
1
,
∅
>
,
<
2
,
∅
>
,
<
3
,
∅
>
,
<
1
,
a
>
,
<
2
,
a
>
,
<
3
,
a
>
}
B \times A = \{ <1, \varnothing > , <2, \varnothing >, <3 , \varnothing >, <1, a> , <2, a> , <3, a> \}
B×A={ <1,∅>,<2,∅>,<3,∅>,<1,a>,<2,a>,<3,a>}
The first element of each ordered pair comes from
B
B
B aggregate , The second element comes from
A
A
A aggregate ;
A
×
A
=
{
<
∅
,
∅
>
,
<
∅
,
a
>
,
<
a
,
∅
>
,
<
a
,
a
>
}
A \times A = \{< \varnothing, \varnothing> , <\varnothing, a> , <a, \varnothing> , <a, a> \}
A×A={ <∅,∅>,<∅,a>,<a,∅>,<a,a>}
The first element of each ordered pair comes from
A
A
A aggregate , The second element comes from
A
A
A aggregate ;
B
×
B
=
{
<
1
,
1
>
,
<
1
,
2
>
,
<
1
,
3
>
,
<
2
,
1
>
,
<
2
,
2
>
,
<
2
,
3
>
,
<
3
,
1
>
,
<
3
,
2
>
,
<
3
,
3
>
}
B \times B = \{ <1, 1> , <1, 2> , <1, 3> , <2, 1> , <2, 2> , <2,3> , <3,1> , <3,2> , <3,3> \}
B×B={ <1,1>,<1,2>,<1,3>,<2,1>,<2,2>,<2,3>,<3,1>,<3,2>,<3,3>}
The first element of each ordered pair comes from
B
B
B aggregate , The second element comes from
B
B
B aggregate ;
3、 ... and 、 Cartesian product property
1. Non exchangeability
A
×
B
≠
B
×
A
A \times B \not= B \times A
A×B=B×A
There are three special cases , Exchangeability is established
①
A
=
B
A = B
A=B
②
A
=
∅
A = \varnothing
A=∅
③
B
=
∅
B = \varnothing
B=∅
2. nonconjugal
(
A
×
B
)
×
C
≠
A
×
(
B
×
C
)
( A \times B ) \times C \not= A \times ( B \times C)
(A×B)×C=A×(B×C)
There are three special cases , The combination is established
①
A
=
∅
A = \varnothing
A=∅
②
B
=
∅
B = \varnothing
B=∅
③
C
=
∅
C = \varnothing
C=∅
3. Distribution rate
A
×
(
B
∪
C
)
=
(
A
×
B
)
∪
(
A
×
C
)
A \times ( B \cup C ) = (A \times B) \cup (A \times C)
A×(B∪C)=(A×B)∪(A×C)
4. The case where the ordered pair is empty
A
×
B
=
∅
⇔
A
=
∅
∨
B
=
∅
A \times B = \varnothing \Leftrightarrow A = \varnothing \lor B= \varnothing
A×B=∅⇔A=∅∨B=∅
Four 、 n Vicat product
n Vicat product :
A
1
×
A
2
×
⋯
×
A
n
=
{
<
x
1
,
x
2
,
⋯
,
x
n
>
∣
x
1
∈
A
1
∧
x
2
∈
A
2
∧
⋯
∧
x
n
∈
A
n
}
A_1 \times A_2 \times \cdots \times A_n = \{ <x_1 , x_2, \cdots , x_n> | x_1 \in A_1 \land x_2 \in A_2 \land \cdots \land x_n \in A_n \}
A1×A2×⋯×An={ <x1,x2,⋯,xn>∣x1∈A1∧x2∈A2∧⋯∧xn∈An}
n
n
n The Cartesian product of sets ,
n
n
n Vicat product result , Each ordered pair has
n
n
n Elements , Each element is separate In the order specified From here
n
n
n A collection of ;
A
n
=
A
×
A
×
⋯
×
A
⏟
n
individual
A^n = \begin{matrix} \underbrace{ A \times A \times \cdots \times A } \\ n individual \end{matrix}
An=
A×A×⋯×An individual
This is a
n
n
n individual aggregate
A
A
A Of
n
n
n Vicat product ;
5、 ... and 、 n The number of Vicat's products
n
n
n The number of Vicat's products :
∣
A
i
∣
=
n
i
,
i
=
1
,
2
,
⋯
,
n
|A_i| = n_i \ , \ i = 1, 2, \cdots , n
∣Ai∣=ni , i=1,2,⋯,n
⇒
\Rightarrow
⇒
∣
A
1
×
A
2
×
⋯
×
A
n
∣
=
n
1
×
n
2
×
⋯
×
n
n
| A_1 \times A_2 \times \cdots \times A_n | = n_1 \times n_2 \times \cdots \times n_n
∣A1×A2×⋯×An∣=n1×n2×⋯×nn
∣
A
i
∣
=
n
i
|A_i| = n_i
∣Ai∣=ni ,
i
=
1
,
2
,
⋯
,
n
i = 1, 2, \cdots , n
i=1,2,⋯,n : Express The first
i
i
i A collection of
A
i
A_i
Ai The number of elements is
n
i
n_i
ni ;
∣
A
1
×
A
2
×
⋯
×
A
n
∣
| A_1 \times A_2 \times \cdots \times A_n |
∣A1×A2×⋯×An∣ : Express
n
n
n The number of result sets of Cartesian products of sets ;
n
1
×
n
2
×
⋯
×
n
n
n_1 \times n_2 \times \cdots \times n_n
n1×n2×⋯×nn :
n
n
n The result of the Cartesian product of sets ;
6、 ... and 、 n Vicat product property
n Vicat product property : And
2
2
2 Vicat's product has similar properties
边栏推荐
- Nat. Comm. | 使用Tensor-cell2cell对细胞通讯进行环境感知去卷积
- 用户体验五要素
- 【刷题篇】 找出第 K 小的数对距离
- [brush questions] most elements (super water king problem)
- 第十届中国云计算大会·中国站:展望未来十年科技走向
- 拆一辆十万元的比亚迪“元”,快来看看里面的有哪些元器件。
- js实现在可视区内,文字图片动画效果
- Export of zip file
- [Blue Bridge Road - bug free code] pcf8591 - code analysis of AD conversion
- Data Lake three swordsmen -- comparative analysis of delta, Hudi and iceberg
猜你喜欢
![[dynamic programming] subsequence problem](/img/d8/020ae959ef53ce097d3a81a0d2d63a.jpg)
[dynamic programming] subsequence problem

国产PC系统完成闭环,替代美国软硬件体系的时刻已经到来
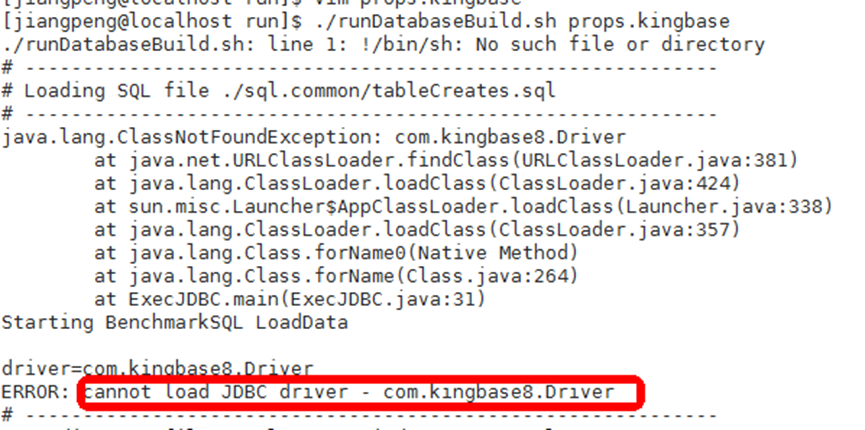
使用BENCHMARKSQL工具对kingbaseES执行灌数据提示无法找到JDBC driver

使用BENCHMARKSQL工具对KingbaseES预热数据时执行:select sys_prewarm(‘NDX_OORDER_2 ‘)报错
Which code editor is easy to use? Code editing software recommendation
JS realizes the animation effect of text and pictures in the visual area

Is it better to speculate in the short term or the medium and long term? Comparative analysis of differences

Mutex and rwmutex in golang

China Mobile Internet of things oneos and onenet were selected in the list of 2021 Internet of things demonstration projects
The latest activation free version of Omni toolbox
随机推荐
[fairseq] error: typeerror:_ broadcast_ coalesced(): incompatible function arguments
『期末复习』16/32位微处理器(8086)基本寄存器
vulnhub HA: Natraj
使用BENCHMARKSQL工具对kingbasees并发测试时kill掉主进程成功后存在子线程未及时关闭
How to process the current cell with a custom formula in conditional format- How to address the current cell in conditional format custom formula?
Competitive product analysis and writing
JMeter starts from zero (III) -- simple use of regular expressions
vim 的实用操作
[dynamic programming] subsequence problem
leetcode:297. Serialization and deserialization of binary tree
Nat. Comm. | 使用Tensor-cell2cell对细胞通讯进行环境感知去卷积
国产PC系统完成闭环,替代美国软硬件体系的时刻已经到来
Dismantle a 100000 yuan BYD "Yuan". Come and see what components are in it.
Deep dive kotlin synergy (19): flow overview
Redraw and reflow
Five elements of user experience
CVPR 2022 | 大連理工提出自校准照明框架,用於現實場景的微光圖像增强
类的基础语法
Mila、渥太华大学 | 用SE(3)不变去噪距离匹配进行分子几何预训练
Interaction free shell programming