Direct select sort and quick sort

Hello everyone ！ In this article, we will talk about direct selection sorting and quick sorting .

1 Direct selection sorting

1.1 The basic idea

Each time, select the smallest from the data elements to be sorted （ Or maximum ） An element of , Store at the beginning of the sequence , Until all the data elements to be sorted are finished .

1.2 Thought process

Here we write a better solution ： Is to find two numbers at a time ( maximal , The smallest ), Put it in the right place .

We put the smallest one on the far left , The largest one is on the far right .

And then start with the next one , By analogy .

1.3 Concrete realization

According to the idea above , We convert it into code ：

We test , It can be found that there is a problem ：

Why is that ？ Let's debug it ：

We can see that the smallest subscript at this time is 1, The largest subscript is 0, Then swap the first one , We'll see ：

At this point, after the exchange ,maxi Point to or 0, But the maximum number at this time 9 Has reached the subscript 1 Location. . So errors will occur , We need to make some adjustments here .

1.4 Time complexity

here , What we write is the optimization method of direct selection sorting , For the first time N, And then there was N-2, And then there was N-4, And then there was N-6… So time complexity is O(N^2), And the bubble sort is N,N-1,N-2,N-3… So direct sorting is better than bubble sorting .
But in order ： Direct selection sorting cannot determine whether it is orderly , Still have to choose layer by layer , And bubble sorting will be fast .

2 Quick sort

2.1 hoare The basic idea

Quick sort is Hoare On 1962 A binary tree structure of the exchange sort method , Its basic idea is ：

Take any element in the element sequence to be sorted as the reference value , According to the sorting code, the set to be sorted is divided into two subsequences , All elements in the left subsequence are less than the base value , All elements in the right subsequence are greater than the base value , Then the leftmost and rightmost subsequences repeat the process , Until all the elements are aligned in their respective positions .

2.2 hoare Thought process

First , Let's take a look at the single trip , The single trip is also divided into three versions ：
The first version ：hoare edition
Choose one key, Usually the first number or the last number .
It is required that the values on the left are all greater than key Small , The values on the right are better than key Big , and key Equal anywhere .
Let's take a look at the dynamic diagram process ：
From the graph we can see ：R Find a comparison key Small ,L Find a comparison key Big , Exchange after finding , Go on . After meeting , Follow the value of the encounter position with key Value exchange of position .

ad locum , Some students may ask a question ：
If the one on the left key The value is smaller than the value at the time of meeting , What should I do ？

This algorithm can avoid this problem as long as it satisfies one condition ：
Going first on the right can guarantee .
It's divided into two situations ：
Case one ：R Stop first ,L Go over and meet R

After the two exchange ,R Go ahead ,R Find a comparison key Small , That is to say 3 stop

then L go , To find a comparison key Big , But one step is like R Equal .

Meeting 3 Than key Small .
The second case ： Just exchanged ,R Go ahead ,R No better than key The small one directly follows L meet .

This situation , It's better than that key Small .

In the above example, we take the left as key, So we want to have on the right key What to do ？

Same thing , Let's go first on the left , The value ratio of the encounter position can be guaranteed key Big .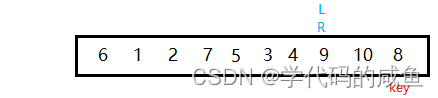

Let's take a look at its dynamic flow chart ：

2.3 hoare Method specific implementation

First , We realize a single trip ：

however , There are two problems in writing this way .
The first question is ：
In the following set of data , It will have an endless cycle .

You can see key and right All are 5, It doesn't satisfy the cyclic condition , Don't go into the cycle .
then key and left All are 5, Nor does it satisfy the cycle condition , Don't go into the cycle .
In exchange for left and right Nothing has changed , So there's a dead cycle .
We can modify it like this ：

The second question is ：
There are still problems after the modification . Let's look at the following set of data ：

here key by 1,right Keep reducing , When right=1 when , Satisfy the cyclic condition , One more time , Just crossed the line .
therefore , We need to add one more condition ：

After a single trip ,key It's in the right place .
If the left side is in order , Order on the right , Then we will be in order as a whole , So how are the left and right sides ordered ？
Divide and conquer solves sub problems .
The results of single pass sorting are as follows ：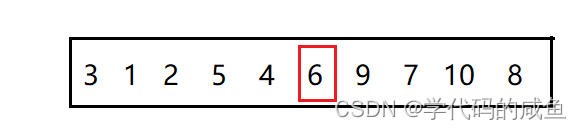

Now? 6 Already in the right place , Now we're going to let 6 The left and right sides of the are also orderly .

After a single sequence , You'll find that 3 And in the right place . Then we divide and conquer 3 On the left and right of .
The whole process is as follows ：

The complete code is as follows ：

2.4 The thought flow of pit digging method

First , Let's take a look at the motion picture ：

then , Let me elaborate on the process of pit excavation ：

First , Let's put the leftmost one on key in , In this way, a pit is formed on the far left . then ,R Let's go and find a better one key Small .

After finding it , We will 5 Put it in the pit . such 5 The location of the pit becomes a new pit .

then L Go and compare key Big , We find 7 after , take 7 Put it in the pit .

R I'm looking for a little girl , find 4 Put it in the pit .

L Find another big , find 9 Put it in the pit .

R I'm looking for a little girl , hold 3 Put it in the pit .

L Find another big , But and R Met , Just put key Put it in the pit , It's over .

such , The single trip process of pit excavation method is over .
Let's take a look at its dynamic flow chart ：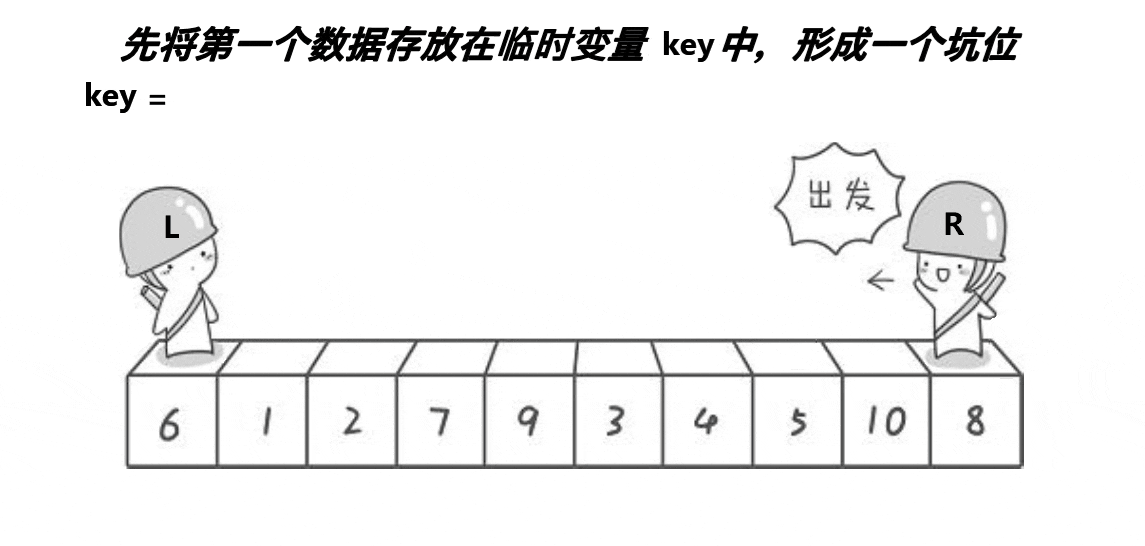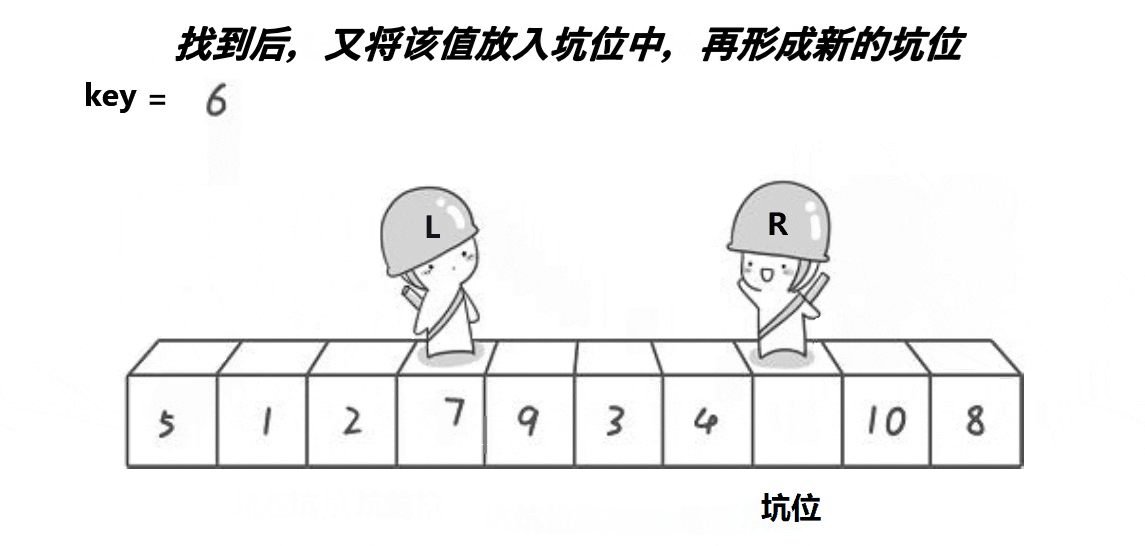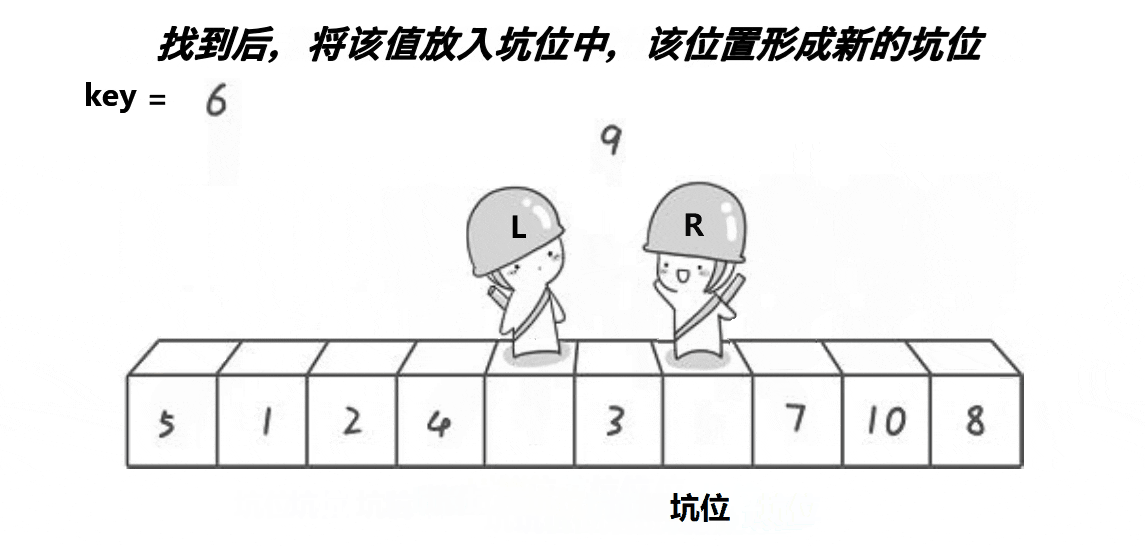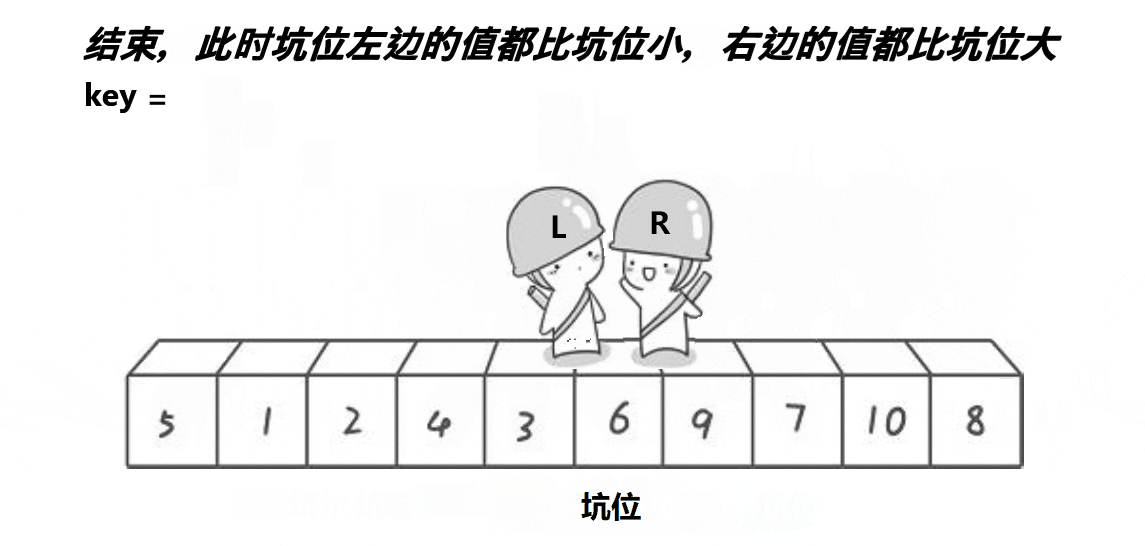

Well, the digging method and hoare What is the difference between law ？
There is no difference in essence . It's just that the digging method is better understood .
1. You don't need to understand why the final encounter is better than key Small .
2. You don't need to understand why the left side does key, Go first on the right .
Because at first we chose the left side as the pit , Then you will naturally think that ,R Go ahead and find Xiao , Fill the hole , When we finally meet, just fill up the hole .

2.5 The concrete implementation of the excavation method

Similar to the above idea ：

2.6 Front and back pointer method thought flow

First , Let's take a look at the dynamic graph process ：

then , Let me talk about the specific process ：
In limine , Let's define a prev The pointer points to the beginning of the sequence , Define a cur Pointer to prev The last position of the pointer .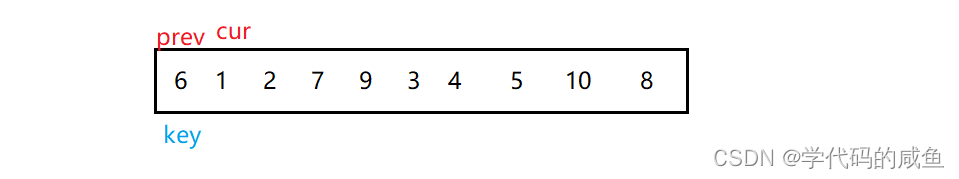

And then determine cur Whether the data pointed to by the pointer is less than key, If less than , be prev Move the pointer back one bit , And then cur Pointer to content exchange . then cur The pointer ++
From the previous set of data , We can see that 1,2, All are less than key Of , and prev Exchange doesn't change anything , When cur Go all the way to 3 The location of ：

here ,prev The pointer should be moved back one bit , And then cur Pointer to content exchange , then cur The pointer ++

here ,cur Point to the 4 Less than 6 Of , Then fear prev Move back a bit , After exchanging content ,cur++

here cur It points to more than key Small ,prev++ after , In exchange for cur Content and prev The content of .

then cur++, here 10 Than key Big ,cur Again ++,8 Than key Big , Again ++

When cur Out of the sequence , In exchange for key and prev The content of .

So the single trip is over .

ad locum ,prev and cur The relationship is ：
1.cur I haven't met anything better than key Large values ,prev Follow closely cur, One before and one after .
2.cur Meet the ratio key After a large value ,prev and cur There is a gap between key The interval of large values .
Let's take a look at its dynamic flow chart ：

2.7 The front and back pointer method is concretely realized

Someone will ask. , If key I chose what to write on the far right ？
We need to prev and cur Dislocation ：

We will cur to left,prev to left-1
The others are the same ,cur Looking for a small ,6 Than 8 Small ,++prev, here prev and cur Number of points 6 equal . therefore cur Again ++

And so on …

here ,cur Point to the 3 Than key Small ,++prev, In exchange for

cur++ Go down in turn .

When cur Point to key when , ends .
But here , We can't exchange directly prev and cur, need prev++ And then exchange key

The code is as follows ：

2.8 Time complexity

What is the time complexity of quick sorting ？
In the best case ： Every election key All median
It means ： After each single sequence ,key In the middle
It will form such ：

On each floor key All need to go n Time , Altogether logN layer , So the time complexity will be ：O(N*logN)
At worst ： Every time you choose key Is the smallest or largest , That is, in an orderly order
That's it ：

So it's an arithmetic sequence , Its time complexity is ：O(N^N)

2.9 How to optimize quick sort

2.9.1 The middle of three numbers key

Choose not the biggest , Not the smallest one .
such , If there is order , We won't choose the biggest and smallest .
therefore , Let's start by writing a function in a triple ：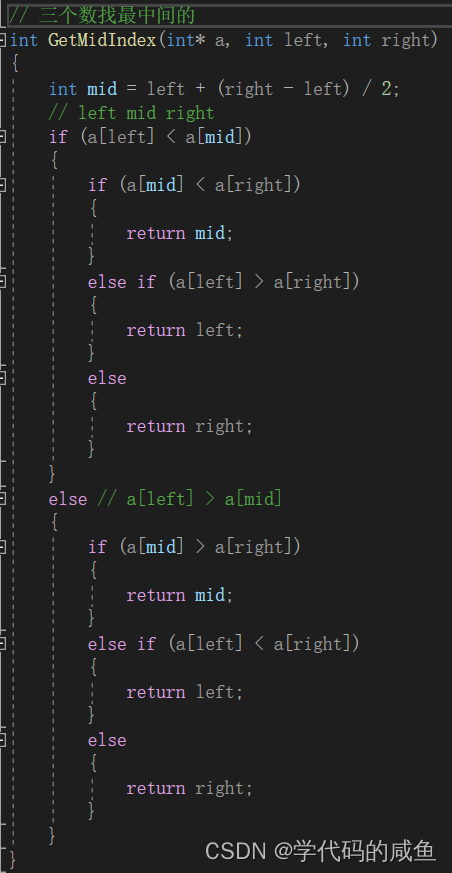

then , Swap the middle number with the leftmost or rightmost number , Other ideas remain the same .

2.9.2 Inter cell optimization

What is inter cell optimization ？
The interval is very small , Stop using the idea of recursive partition and make it orderly , Instead, insert sorting is directly used to sort cells , Reduce recursive calls .
What does that mean ？ Let's take a look at the quick row recursive call expansion diagram ：

hypothesis , We have 1000 Number , There is a 10 layer , The last layer is 1 Number , Also have 2^9 individual . The penultimate layer is 3 Number , Yes 2 ^8 individual . therefore , We can change the recursion of the following layers to direct insertion sorting ：

void QuickSort(int* a, int begin, int end)
{
    
	//  Inter cell direct insertion sequencing control is in order 
	// When the number of intervals is less than or equal to 10 Number of hours , Just insert the sort directly 
	if (end - begin + 1  <= 10)
	{
    
		InsertSort(a + begin, end - begin + 1);
	}
	else
	{
    
		int keyi = PartSort3(a, begin, end);
		// [begin, keyi-1]keyi[keyi+1, end]
		QuickSort2(a, begin, keyi - 1);
		QuickSort2(a, keyi + 1, end);
	}
	
}

Because it's a closed interval , The number is subtracted from the two +1

The beginning of each insertion sort , We should be a+begin