当前位置:网站首页>Parameter estimation -- Chapter 7 study report of probability theory and mathematical statistics (point estimation)
Parameter estimation -- Chapter 7 study report of probability theory and mathematical statistics (point estimation)
2022-06-27 01:50:00 【IOT classmate Huang】
Parameter estimation ——《 Probability theory and its mathematical statistics 》 Chapter VII study report ( Point estimation )
List of articles
Preface
It's been a long time , I have been busy with other subjects recently ,emmm Make a study report on Chapter 7 before the end of the term .
Because of the setting of teaching , This time, only the point estimation in Chapter 7 parameter estimation has been done , A full version will be released if there is a chance in the future .
The tutorial is the same as before , The fourth edition of Zhejiang University + The fifth edition .
MindMap

The point estimate is divided into Moment estimation method and Maximum likelihood estimation Two kinds of .
Moment estimation method
We learned a little about moments in Chapter 4 , For example, the origin moment 、 Central moment, etc . ad locum , We use Sample moment To estimate Total moment , Then the estimation of relevant parameters .
We use random variables X The type of , That is, discrete type or continuous type , To divide .
if X by discrete :
branch cloth Law by : P { X = x 0 } = p ( x ; θ 1 , θ 2 , . . . , θ k ) , this in Of θ i , Just yes I People want seek Of stay Estimate meter ginseng Count . have to To total body X Of front k rank Moment : μ l = E ( X l ) = ∑ x ∈ R x x l p ( x ; θ 1 , θ 2 , . . . , θ k ) The law of distribution is :P\{X=x0\} = p(x;\theta_1, \theta_2, ..., \theta_k), there \theta_i, It is the parameter to be estimated that we require . \\ Get overall X Before k moment :\mu_l = E(X^l) = \sum_{x\in R_x}{x^lp(x;\theta_1, \theta_2, ...,\theta_k)} branch cloth Law by :P{ X=x0}=p(x;θ1,θ2,...,θk), this in Of θi, Just yes I People want seek Of stay Estimate meter ginseng Count . have to To total body X Of front k rank Moment :μl=E(Xl)=x∈Rx∑xlp(x;θ1,θ2,...,θk)
if Continuous type :
General rate The secret degree : f ( x ; θ 1 , θ 2 , . . . , θ k ) μ l = E ( X l ) = ∫ − ∞ ∞ x l f ( x ; θ 1 , θ 2 , . . . , θ k ) d x Probability density :f(x;\theta_1, \theta_2, ..., \theta_k) \\ \mu_l = E(X^l) = \int_{-\infty}^\infty{x^lf(x;\theta_1, \theta_2, ..., \theta_k)dx} General rate The secret degree :f(x;θ1,θ2,...,θk)μl=E(Xl)=∫−∞∞xlf(x;θ1,θ2,...,θk)dx
The sample moment is
A l = 1 n ∑ i = 1 n X i l A_l = \frac{1}{n}\sum_{i = 1}^{n}{X_i^l} Al=n1i=1∑nXil
The so-called moment estimation method Is to use the sample moment as the total moment An estimate .
Solution steps
- Let's start with the moment , The number of moments listed here depends on the number of parameters we are going to estimate .
- Then we calculate the formula of the parameter about the moment .
- Replace the above total moment with the sample moment .
- Finally, remember to add a sharp corner mark on the estimated parameters .
Maximum likelihood estimation
Let's discuss it separately and continuously .
discrete
Distribution law
P { X = x } = p ( x ; θ ) , θ ∈ Θ set up X 1 , X 2 , . . . , X n Of One individual sample Ben value , I People can With know Avenue X i , i ∈ [ 1 , k ] Of General rate P\{X=x\} = p(x;\theta), \theta \in \Theta \\ set up X_1, X_2, ..., X_n A sample value of , We can know X_i,i\in [1, k] Probability P{ X=x}=p(x;θ),θ∈Θ set up X1,X2,...,Xn Of One individual sample Ben value , I People can With know Avenue Xi,i∈[1,k] Of General rate
You can get
P { X 1 = x 1 , X 2 = x 2 , . . . , X n = x n } = L ( θ ) = L ( x 1 , x 2 , . . . , x n ; θ ) = ∏ i = 1 n p ( x i ; θ ) , θ ∈ Θ P\{X_1 = x_1, X_2 = x_2, ..., X_n = x_n\} = L(\theta) = L(x_1, x_2, ..., x_n;\theta) = \prod_{i=1}^{n}p(x_i;\theta), \theta\in \Theta P{ X1=x1,X2=x2,...,Xn=xn}=L(θ)=L(x1,x2,...,xn;θ)=i=1∏np(xi;θ),θ∈Θ
This function L Namely Of the sample Likelihood function .
The reason why this method is called Maximum likelihood estimation , That's what we took θ Estimated parameter value of , Is a maximum parameter value
L ( x 1 , x 2 , . . . , x n ; θ ^ ) = max θ ∈ Θ L ( x 1 , x 2 , . . . , x n ; θ ) L(x_1, x_2, ...,x_n; \hat{\theta}) = \max_{\theta\in\Theta}{L(x_1, x_2, ... , x_n; \theta)} L(x1,x2,...,xn;θ^)=θ∈ΘmaxL(x1,x2,...,xn;θ)
Continuous type
Probability density
∏ i = 1 n f ( x i ; θ ) \prod_{i=1}^{n}{f(x_i;\theta)} i=1∏nf(xi;θ)
Likelihood function
L ( θ ) = L ( x 1 , x 2 , . . . , x n ; θ ^ ) = ∏ i = 1 n f ( x i ; θ ) L(\theta)=L(x_1, x_2, ...,x_n; \hat{\theta}) =\prod_{i=1}^{n}{f(x_i;\theta)} L(θ)=L(x1,x2,...,xn;θ^)=i=1∏nf(xi;θ)
If we take a logarithm and then take the derivative , You can get
d d θ l n L ( θ ) = 0 \frac{d}{d\theta}{lnL(\theta)} = 0 dθdlnL(θ)=0
You get Log likelihood equation .
Why do you take derivatives ? Because you want to take the maximum , So the derivative is 0 The situation of , Of course, minima and bounds are ignored here .
Basically, there is little difference between the steps and the moment estimation , It's also calculation , It's just more about deriving and solving equations .
In the case of multiple parameters , Just find the partial derivative .
边栏推荐
猜你喜欢
我靠副业一个月挣了3W块:你看不起的行业,真的很挣钱!

Online text digit recognition list summation tool
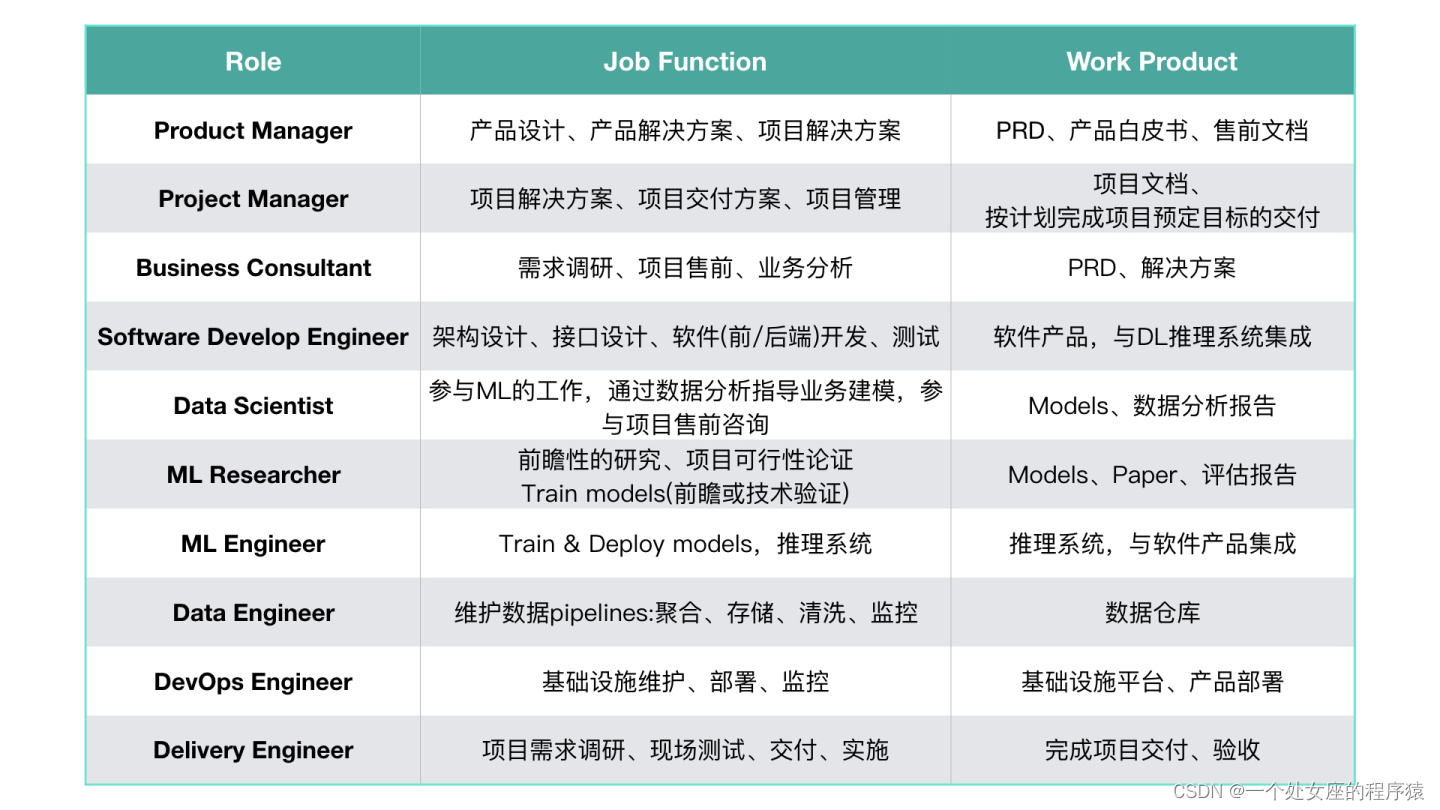
Ml: a detailed introduction to the division of the top ten roles, backgrounds, responsibilities and outputs of the machine learning engineering team

你的case真的pass了吗?

Browser cache

Binary tree OJ problem

SystemVerilog simulation speed increase

ThreadLocal详解

p5.js死亡星球
Summary of config mechanism and methods in UVM (2)
随机推荐
hibernate 根据方言生成sql
Cookie, sessionstorage, localstorage differences
Reporting Classes中uvm_report_server的get_severity_count和get_server用法
lottie.js创意开关按钮动物头像
Reading a book in idea is too much!
Recursion will make strtok more attractive
Oracle/PLSQL: Replace Function
“所有专业都在劝退”,对大学生最友好的竟然是它?
Summary of config mechanism and methods in UVM (2)
get_sequencer的用法总结
SystemVerilog仿真速率提升
按键控制LED状态翻转
Oracle/PLSQL: Rtrim Function
getReader() has already been called for this request
Memcached basics 14
Oracle/PLSQL: Length Function
D's appendto packaging
Would rather go to 996 than stay at home! 24 years old, unemployed for 7 months, worse than work, no work
别被洗脑了,这才是90%中国人的工资真相
Oracle/PLSQL: To_ Clob Function