IV Transforming regular expressions into finite state automata: DFA minimization

original text :https://study.163.com/course/courseMain.htm?courseId=1002830012

From the picture above , node ,4,6,7 It can be merged into one node . Or say , We can put nodes 4,6 Remove without affecting the function of the state machine . The purpose of this section is to discuss how to achieve DFA Optimization function of .

DFA Description of minimization algorithm ：
1. Divide all state nodes into two partitions , The receiving status is a partition , The non receiving status is a partition ：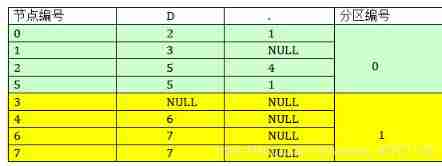

node 0,1,2,5 Is a non receiving node , They are put into one partition , Partition number 0.
node 3, 4, 6, 7 Is the receiving node , They are put into one partition , Partition label 1.

2. According to the jump after each status node corresponds to the input character , Proceed to the next partition . Let's first look at the case where the input character is a numeric character , That is to say, look at the D Column , node 0,2,5 The corresponding input is D when , Their jump status is 2,5,5, These states are in the partition 0, That is, nodes 0,2,5 When the corresponding input is a numeric character , Jump to partition 0, node 1 Input D when , Jump to state 3, state 3 In the district 1, thus , state 1 From partition 0 Take out the , Separate into a partition . The same goes for partitions 1 Nodes in , state 3, The corresponding input is D when , Jump to NULL, state 4,6,7 Corresponds to the input D, Jump to node 6,7,7, node 6,7,7 All in the partition 1, therefore , At this point, you can change the status 3 Take it out , Form a separate partition , So there is ：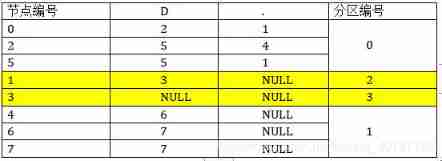

After the transformation , node 2 In a separate partition, the label is 2, node 3 A separate division number 3.

3. We are looking at the input character as ”.” The situation of , Partition 0 Status point in 0 Receive character ”.” Then jump to the state 1, node 5 Jump to state 1, in other words , Status point 0,5 Receive character ”.” After that, they are all transferred to the same partition 2, Status point 2 receive ”.” Then jump to the node 4, node 4 In the district 1, therefore , Status point 2 From partition 0 Peel away , Because of the zoning 1,2,3 None of the status points in receive characters ”.” So they don't deal with it , So there is the following table ：

4. Based on the above segmentation , We'll never do it again , See if you can create new partitions , The input is D when , Partition 0 Status node in 0 Jump to state 2, state 2 In the district 4, The status node jumps 5 Jump to state 5, state 5 In the district 0, therefore , Partition 0 Two nodes in 0,5 Must be separated ：

5. Based on the above table , Let's make different input , Nodes in each partition can no longer be partitioned , So the algorithm is over .

According to the split situation , Let's take the transfer relationship between points , Change to the transfer relationship between partitions , We get new DFA:

node 0 In the district 0, Input D Then jump to the node 2, node 2 In the district 4, The input character ”.”, Jump to state 1, state 1 In the district 2, So there is ：
0-(D)->4, 0-.->2

node 5 In the district 5, Input D Then jump to the node 5, node 5 In the district 5, Input ”.” Then jump to the node 1, node 1 In the district 2, So there is ：
5-(D)->5, 5-.->2

node 2 In the district 4, Input D Jump node 5, node 5 In the district 5, Input ”.” Jump to node 4, node 4 In the district 1, So there is ：
4-(D)->5, 4-.->1

node 1 In the district 2, Input D Jump to node 3, node 3 In the district 3, So there is ：
2-(D)->3

node 4,6,7 In the district 1, Input D The post jump points are all in the partition 1, So there is ：
1-(D)->1

So we get the optimized DFA：