当前位置:网站首页>CodeCraft-22 and Codeforces Round #795 (Div. 2) 题解
CodeCraft-22 and Codeforces Round #795 (Div. 2) 题解
2022-06-12 09:03:00 【andyc_03】
A. Beat The Odds
【题意】
给定一个序列,问最少需要删掉几个数字能够使得任意两个相邻的数和是偶数
【分析】
删除全部偶数或奇数即可
【代码】
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=2e6+5;
int n;
int main()
{
int T; scanf("%d",&T);
while(T--)
{
scanf("%d",&n);
int x,gsa=0,gsb=0;
for(int i=1;i<=n;i++)
{
scanf("%d",&x);
if(x&1) gsa++;
else gsb++;
}
printf("%d\n",min(gsa,gsb));
}
return 0;
}B. Shoe Shuffling
【题意】
n个人,给定每个人的鞋子大小,请求出一个鞋子分配方式(排列),使得每个人穿的都不是自己本来的鞋子,且分到的鞋子不小于自己原本的鞋子大小
不存在输出-1
【分析】
能够互相交换鞋子的大小一定是相等的,因为有不相等的参与互相交换的话,一定会有人分到比自己原来的鞋子小的情况
所以我们直接把鞋子大小相等的人,编号串一位即可
【代码】
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1e5+5;
int n;
struct shoes
{
int sz,id;
}a[maxn];
bool cmp(shoes x,shoes y)
{
if(x.sz==y.sz) return x.id<y.id;
return x.sz<y.sz;
}
int res[maxn];
int main()
{
int T; scanf("%d",&T);
while(T--)
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i].sz);
a[i].id=i;
}
int flag=0;
for(int i=1,j=1;i<=n;i=j+1)
{
while(a[j+1].sz==a[i].sz && j<n) j++;
if(j==i)
{
flag=1;
break;
}
for(int k=i;k<j;k++)
res[a[k].id]=a[k+1].id;
res[a[j].id]=a[i].id;
}
if(flag) printf("-1\n");
else{
for(int i=1;i<=n;i++) printf("%d ",res[i]);
printf("\n");
}
}
return 0;
}C. Sum of Substrings
【题意】
给定一个01序列S,可以选择k次交换相邻两位置,最小化f(S)
f(S)为序列中相邻两位的十进制之和
'01'=1 '11'=11 '10'=10
【分析】
考虑不在两头的每个1能带来11的贡献(分别作为个位和十位)
要最小化,如果两头有0,我们可以把中间的1挪到两侧
优先到右侧,最右侧的贡献是1,最左侧的贡献是10
注意一些corner case和细节即可
【代码】
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1e5+5;
int n,k;
char s[maxn];
int main()
{
int T; scanf("%d",&T);
while(T--)
{
scanf("%d%d",&n,&k);
scanf("%s",s+1);
int f1=0,f2=0;
if(s[1]=='1') f1=1;
if(s[n]=='1') f2=1;
int now=f1*10+f2;
for(int i=2;i<n;i++) if(s[i]=='1') now+=11;
int posa=2,posb=n,xz=n;
if(!f2)
{
while(posb && s[posb]=='0') posb--;
if(posb>1 && n-posb<=k)
{
k-=n-posb;
now-=10;
xz=posb;
}
if(posb==1 && k>=n-1)
{
k-=n-1;
now-=9;
}
}
if(!f1)
{
while(s[posa]=='0' && posa<=n) posa++;
if(posa<xz && posa-1<=k)
now--;
}
printf("%d\n",now);
}
return 0;
}D. Max GEQ Sum
【题意】
给定一个序列,询问是否存在点对(i,j),i<j,使得区间[i,j]的最大值大于等于区间数值的和
【分析】
考虑对于每个正数的位置pos作为区间mx的情况,先向左和向右二分出能选到的最左和最右的范围
这里可以用st表+二分 O(logn)实现,我选择了更好写的方式,从大到小考虑正数,这样就可以把位置插入到set内二分了 也是O(logn)
找到l-r范围后,我们要在这个区间内寻找包含pos的最大区间和是多少
可以用线段树每个点表示前缀和,维护mx和mn
在l到pos-1中寻找min作为左端点左侧一个的位置,在pos到r-1寻找max作为右侧的位置即可
【代码】
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll inf=1e17;
const int maxn=2e5+5;
int n;
ll a[maxn],sum[maxn];
int cnt;
struct zheng
{
int id;
ll val;
}b[maxn];
bool cmp(zheng x,zheng y)
{
if(x.val==y.val) return x.id<y.id;
return x.val>y.val;
}
set <int> pos;
struct seg
{
ll mx,mn;
}tr[maxn<<2];
void build(int now,int l,int r)
{
if(l==r)
{
tr[now].mn=sum[l];
tr[now].mx=sum[l];
return;
}
int mid=l+r>>1;
build(now<<1,l,mid);
build(now<<1|1,mid+1,r);
tr[now].mn=min(tr[now<<1].mn,tr[now<<1|1].mn);
tr[now].mx=max(tr[now<<1].mx,tr[now<<1|1].mx);
}
ll query_min(int now,int l,int r,int L,int R)
{
if(L>R) return inf;
if(l>=L && r<=R) return tr[now].mn;
int mid=l+r>>1;
ll res=inf;
if(L<=mid) res=min(res,query_min(now<<1,l,mid,L,R));
if(mid<R) res=min(res,query_min(now<<1|1,mid+1,r,L,R));
return res;
}
ll query_max(int now,int l,int r,int L,int R)
{
if(L>R) return -inf;
if(l>=L && r<=R) return tr[now].mx;
int mid=l+r>>1;
ll res=-inf;
if(L<=mid) res=max(res,query_max(now<<1,l,mid,L,R));
if(mid<R) res=max(res,query_max(now<<1|1,mid+1,r,L,R));
return res;
}
int main()
{
int T; scanf("%d",&T);
while(T--)
{
scanf("%d",&n);cnt=0;
for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
int flag=0;
for(int i=1;i<=n;i++)
{
sum[i]=sum[i-1]+a[i];
if(a[i]>0)
{
cnt++;
b[cnt].id=i;
b[cnt].val=a[i];
}
}
for(int i=1;i<=n*2;i++) tr[i].mn=inf,tr[i].mx=-inf;
build(1,0,n);
sort(b+1,b+cnt+1,cmp);
pos.clear();
pos.insert(0); pos.insert(n+1);
for(int i=1;i<=cnt;i++)
{
int now=b[i].id;
set <int> ::iterator it=(pos.upper_bound(now));
it--;
int l=(*it),r=*(pos.upper_bound(now));
ll qmin=query_min(1,0,n,l,now-1);
ll qmax=query_max(1,0,n,now,r-1);
if(b[i].val<qmax-qmin)
{
flag=1;
break;
}
pos.insert(now);
}
if(flag==1) printf("NO\n");
else printf("YES\n");
}
return 0;
}E. Number of Groups
【题意】
给定n个区间,每个区间有一个颜色0/1,我们称两个区间是一组的当且仅当两个区间有重叠部分且颜色不同,问一共有多少个组
【分析】
我们使用并查集维护分组情况,然后扫描线,维护两个set,分别存放两个颜色的区间(左端点已经遍历过)
每次扫描到一个节点:
如果是起始点,放入相应的set中,把它和另一个颜色所有元素merge,另一个颜色的set只留下终止点最靠右的那个区间
如果是终止点,从set中删除即可
注意同一坐标的现插入后删除的顺序问题!
【代码】
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> PII;
const ll inf=1e17;
const int maxn=2e5+5;
#define mp make_pair
int n,cnt,fa[maxn];
struct line
{
int id,pos,epos,col,opt;
}a[maxn];
bool cmp(line x,line y)
{
if(x.pos==y.pos) return x.opt>y.opt;
return x.pos<y.pos;
}
set <PII> s[2];
int find(int x)
{
if(x==fa[x]) return x;
return fa[x]=find(fa[x]);
}
void merge(int x,int y)
{
int fx=find(x),fy=find(y);
if(fx==fy) return;
fa[fx]=fy;
}
int main()
{
int T; scanf("%d",&T);
while(T--)
{
scanf("%d",&n);
int c,l,r; cnt=0;
for(int i=1;i<=n;i++)
{
scanf("%d%d%d",&c,&l,&r);
a[++cnt]=(line){i,l,r,c,1};
a[++cnt]=(line){i,r,r,c,-1};
fa[i]=i;
}
sort(a+1,a+cnt+1,cmp);
s[0].clear(); s[1].clear();
for(int i=1;i<=cnt;i++)
{
if(a[i].opt==1)
{
s[a[i].col].insert(mp(a[i].epos,a[i].id));
while(s[a[i].col^1].size()>1)
{
auto [r,id]=*s[a[i].col^1].begin();
merge(id,a[i].id);
s[a[i].col^1].erase(mp(r,id));
}
if(s[a[i].col^1].size()==1)
merge(a[i].id,s[a[i].col^1].begin()->second);
}
else
{
s[a[i].col].erase(mp(a[i].epos,a[i].id));
}
}
int ans=0;
for(int i=1;i<=n;i++) if(fa[i]==i) ans++;
printf("%d\n",ans);
}
return 0;
}F. K-Set Tree
【题意】
定义f(u,S)表示以u为根时,包含点集S内所有节点的根子树点数最小是多少
这里的根子树定义为连通且每个点到叶子路径上的所有点都在子树内
求对于所有点u和|S|=k的点集S的f(u,S)的和
【分析】
考虑每个点为根,可以使用换根dp进行计算,那么我们就把问题拆分成了两部分:
1.根固定为r的时候如何dp计算贡献
2.如何换根更新旧根和新根的dp值
对于问题1,我们对于每个点记录g[u]表示u子树是大小为k的点集的答案的方案数,那么对于固定根r,ans[r]=sum of g[u]*sz[u]
利用容斥进行计算
g[u]=C(k,sz[u]) - (v=son of u) C(k,sz[v])
对于问题2,直接画画图考虑一下变化的部分即可
具体可见代码,自认还算清晰
【代码】
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=2e5+5;
const ll mod=1e9+7;
int n,k;
ll sz[maxn],g[maxn];
vector <int> G[maxn];
ll fac[maxn],inv[maxn],rfac[maxn];
void init()
{
fac[0]=inv[0]=fac[1]=inv[1]=rfac[0]=1;
for(int i=2;i<=n;i++)
{
fac[i]=fac[i-1]*i%mod;
inv[i]=mod-mod/i*inv[mod%i]%mod;
}
for(int i=1;i<=n;i++) rfac[i]=rfac[i-1]*inv[i]%mod;
}
ll C(int x,int y)
{
if(x<y) return 0;
return fac[x]*rfac[y]%mod*rfac[x-y]%mod;
}
ll ans;
void dfs(int u,int fa)
{
sz[u]=1;
ll delta=0;
for(auto to:G[u])
{
if(to==fa) continue;
dfs(to,u);
sz[u]+=sz[to];
delta=(delta+C(sz[to],k))%mod;
}
g[u]=(C(sz[u],k)-delta+mod)%mod;
ans=(ans+g[u]*sz[u])%mod;
}
ll res=0;
void ddfs(int u,int fa)
{
res=(res+ans)%mod;
for(auto to:G[u])
{
if(to==fa) continue;
ll tmpszu=sz[u],tmpszv=sz[to];
ll tmpgu=g[u],tmpgv=g[to],tmp=ans;
sz[u]-=sz[to]; sz[to]=n;
g[u]=(g[u]-C(tmpszu,k)+mod)%mod;
g[u]=(g[u]+C(sz[u],k))%mod;
g[u]=(g[u]+C(tmpszv,k))%mod;
g[to]=(g[to]-C(tmpszv,k)+mod)%mod;
g[to]=(g[to]+C(sz[to],k))%mod;
g[to]=(g[to]-C(sz[u],k)+mod)%mod;
ans=(ans-tmpszu*tmpgu%mod+mod)%mod;
ans=(ans-tmpszv*tmpgv%mod+mod)%mod;
ans=(ans+g[u]*sz[u]%mod)%mod; ans=(ans+g[to]*sz[to]%mod)%mod;
ddfs(to,u);
g[u]=tmpgu; g[to]=tmpgv; sz[u]=tmpszu; sz[to]=tmpszv; ans=tmp;
}
}
int main()
{
scanf("%d%d",&n,&k);
int x,y;
init();
for(int i=1;i<n;i++)
{
scanf("%d%d",&x,&y);
G[x].push_back(y);
G[y].push_back(x);
}
dfs(1,0);
ddfs(1,0);
printf("%lld\n",res);
return 0;
}边栏推荐
- 128. 最长连续序列-哈希表
- mySql学习记录——二、mySql建表命令
- Sword finger offer II 016 Longest substring without repeating characters - sliding window
- Technology cloud report: how will the industrial Internet rebuild the security boundary in 2022?
- MySQL learning record - II. MySQL create table command
- (12) Interactive component selectable
- [character set 8] char8_ t、char16_ t、char32_ t、wchar、char
- (js)三位用逗号隔开,保留两位小数(or 四舍五入取整)
- 2022.6.9-----leetcode. four hundred and ninety-seven
- Redis installation test
猜你喜欢
【字符集七】汉字的宽字符码和多字节码分别是多少

xshell启动遇到“由于找不到mfc110.dll,无法继续执行代码的解决方法”

《MATLAB 神经网络43个案例分析》:第8章 GRNN网络的预测----基于广义回归神经网络的货运量预测
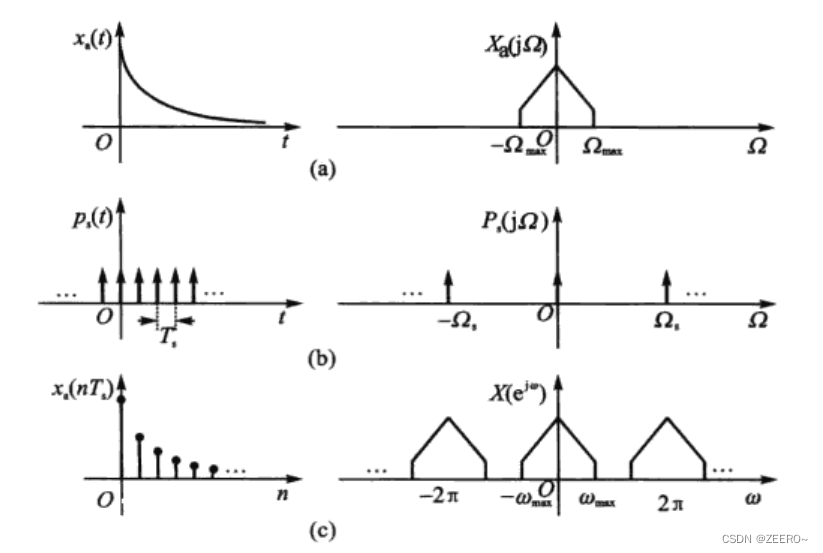
Popular understanding of time domain sampling and frequency domain continuation
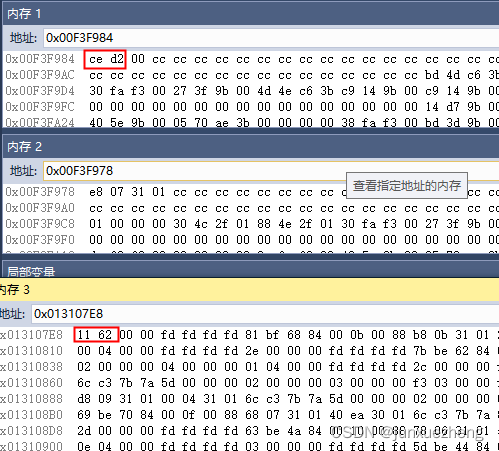
Implementing architecture caching in MySQL under redis server environment

Description of string

Problems that cannot be resolved by tar command

MySQL learning record - II. MySQL create table command
![[advanced pointer I] character array & array pointer & pointer array](/img/ea/150b2162e4e1641eee7e852935d101.png)
[advanced pointer I] character array & array pointer & pointer array

Notes on data mining in Tsinghua University (1)
随机推荐
长安链节点证书、角色、权限管理介绍
《MATLAB 神经网络43个案例分析》:第7章 RBF网络的回归--非线性函数回归的实现
Background location case 1
[character set 8] char8_ t、char16_ t、char32_ t、wchar、char
IDEA新版UI申请方法+无测试资格使用方法及相关介绍
解压缩zip文件的工具类
consul 配置相关
Unittest测试框架
分库分表会带来读扩散问题?怎么解决?
Flink passes in custom parameters or profiles
UMI packaging and subcontracting, and compressing to gzip
Construction of memcached cache service under Linux:
Priority issues
清华大学数据挖掘笔记(一)
About weights exercise
Wechat applet image saving function
Knowledge points of 2022 system integration project management engineer examination: project cost management
Introduction to applet cloud development -- questionnaire evaluation applet practice (7)
Cookies and sessions
(十二)交互组件Selectable