Popular understanding of time domain sampling and frequency domain continuation

Talk about continuous signals $x_a(t)$ And impulse string signal $p_s(t)$ Multiply , The discrete-time signal can be obtained $x(n)$, therefore , There is a formula ：
$$x(n)=x_a(t){|}_{t=n{T}_s}=x_a(t)p_s(t)=x_a(t)\sum _{n=-\infty }^{\infty }\delta (t-n{T}_s)$$
The sampling period is $T_s$, We use it $X_a(j\Omega )$ To represent an analog signal $x_a(t)$ The spectrum of , use $X(e^{jw})$ To represent discrete signals $x(n)$ The spectrum of , according to Fourier Change the formula ,
$$\begin{gathered} X_a(j\Omega )={\int }_{-\infty }^{\infty }{x}_a(t)e^{-j\Omega t}dt \\ X(e^{jw})=\sum _{n=-\infty }^{\infty }x(n)e^{-jwn} \end{gathered}$$
The schematic diagram is shown below ：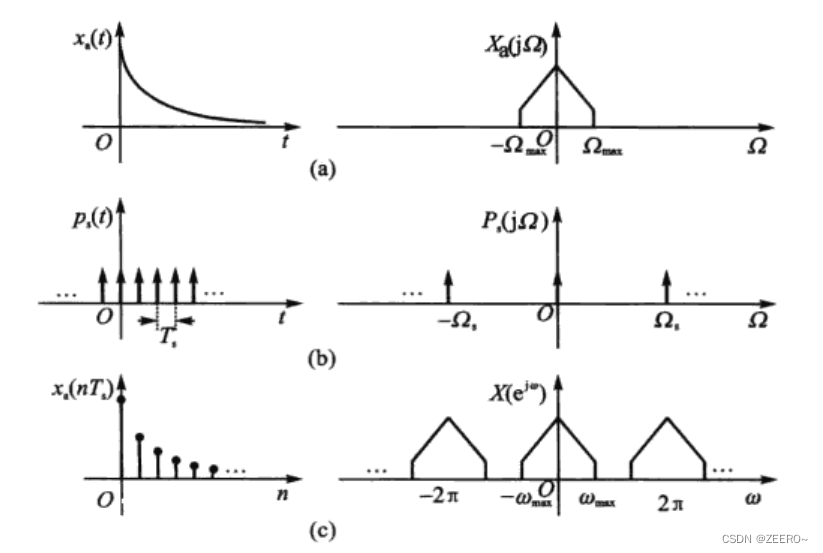

Above picture , We assume that $x_a(t)$ Is band limited signal , A signal with a finite frequency band , We hope to find out $X_a(j\Omega )$ And $X(e^{jw})$ The difference and connection between .
We know , Discrete signal can be regarded as a special continuous signal , Put it Fourier The transformation is recorded as $X_s(j\Omega )$. From the relationship between analog frequency and digital frequency ,$X_s(j\Omega )$ And $X(e^{jw})$ The relationship between is
$$X(e^{jw})=X_s(j\Omega ){|}_{\Omega =w/T_s}$$
About the relationship between analog frequency and digital frequency , Look at this article The relationship between analog frequency and digital frequency .
Let's move on to , We all know , Time domain multiplication is equal to frequency domain convolution , Expressed by a mathematical formula
$$X_s(j\Omega )=X_a(j\Omega )\ast P_s(j\Omega )$$
, among $P_s(j\Omega )$ Is the... Of the impulse signal string Fourier Transformation .

Reference material

《 Put this to use ： In simple terms, digital signal processing 》 Jiangzhihong