[compilation principle] understand BNF

BNF normal form

The following is from Baidu Encyclopedia ：

The Bakos paradigm （BNF） The syntax described is context independent . It has simple syntax , Express clearly , It is convenient for syntax analysis and compilation .

The algorithm used for source code parsing is BNF Or its improved algorithm .

What is context free grammar ？

You can refer to another article in this column ：【 Compiler principle 】 What is context free grammar ？

Why learn BNF？

because BNF It is a concrete method to describe context free theory , So we need to learn BNF. Think of it as a programming language that describes syntax , adopt BNF This grammar can be materialized 、 Formulaize 、 make scientific , Is a necessary condition for code parsing .

How to learn BNF？
BNF It is one of the difficulties in front-end code parsing , For those who are not sensitive to Mathematics , You may find the formula difficult to understand . In fact, we can master it from the perspective of computer science , Express your knowledge in simple language .

example ： Four arithmetic BNF,<> Represents a non leaf node ,| To express or relate to ,:= It means equal to .

<expr> ::= <expr> + <term>
         | <expr> - <term>
         | <term>

<term> ::= <term> * <factor>
         | <term> / <factor>
         | <factor>

<factor> ::= ( <expr> )
           | Num

so ,BNF In essence, it is tree decomposition , It breaks down into a tree called AST The abstract syntax tree of .
About AST, You can refer to another article in this column ： What is? AST？

---

Generative formula

BNF The expression in is called production . Production is an equation that expresses the decomposition rules of grammar . Such as

The sentence = Lord + Predicate + Bin

The purpose of describing grammar rules in production is to facilitate calculation , Production can be seen as a mathematical model of grammar .

The characteristic of production is Continue to break down . This feature is the same as the tree in the data structure .
By analogy , Yes ：

• Each production is a subtree , When writing compilers , Each subtree corresponds to an analytic function .
• Leaf nodes are called Terminator , Non leaf nodes are called non-terminal .

---

recursive

Production is divided into recursive and non recursive , If a production expresses itself by itself, recursion will occur .
Recursively call your own definition to define yourself , Is endless .
such as ：

• GNU Name of the project GUN NOT UNIX;
• A=A’b’（'b’ Represents a character constant b）.

ask ：
Clearly, the code text is finite in length , Why introduce recursion to parse , It's complicated ？

answer ：
The actual code text is really finite .
however , Recursive production simply defines a calculation formula , Through this formula , You can generate an infinite number of strings . for example , The four operations can be described by recursive production , It means that you can write countless four arithmetic expressions of any length , It is to use a formula to describe all situations , It is the abstraction and induction of actual rules . In the actual , It is impossible for us to write a section of parsing code for every four arithmetic expressions , By contraries , All four expressions are parsed using the same parser .

Recursion is divided into left recursion and right recursion , The following are described visually in the form of graphics .

---

Left recursion

The figure above shows , The production continues to the left , Can't end , It will never end , So it's called left recursion .
Obviously, left recursion cannot decompose finite leaf nodes . In especial , It can never get the first leaf node . Because the left side recursively generates a new left leaf node . This conclusion is very important , want Keep in mind .

---

Right recursion

Contrary to left recursion , Right recursion has the first leaf node , No last leaf node .

---

How to judge whether a production has recursion ？

The schematic diagram is as follows ：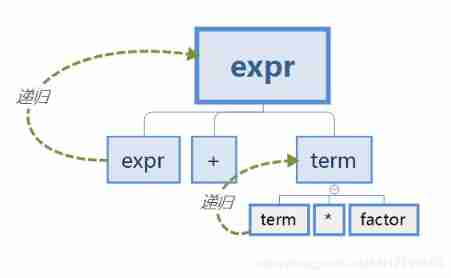

The child node is the same as the parent node Direct left recursion , The ancestors of child nodes and non parent nodes are the same Indirect left recursion .

---

Why recursion can eliminate ？

because some Left and right recursion can be transformed into each other , Note that not all left and right recursions can be transformed into each other . What are the details , We will talk about , Is a recursive expression that contains terminator branches , The terminator is the bridge of transformation .

---

Why only need to eliminate left recursion ？

We need to clarify the important meaning of the first leaf node ： The first node is the starting point of the syntax , So the first node is very important , If there is no first leaf node , Then it will never be possible to determine which character this syntax starts with . So there is a grammar of left recursion , It cannot be parsed by program , Such a program cannot be implemented .

By contraries , Right recursion has the first leaf node , No last leaf node . With the first leaf node, you can determine which character the syntax starts with , But I don't know when the grammar ends .

however , In actual parsing , Because the parsed text is finite , So right recursion must stop . besides , Because right recursion must have a starting symbol , So when parsing text , Once a non starter string is encountered , It will also stop parsing . in other words , Right recursion can automatically ensure the correctness of syntax , And not infinite recursion .

Sum up , Only left recursion needs to be eliminated .

---

How to eliminate left recursion

At present, we can't even write production , How to eliminate ？ So let's put aside the problem of eliminating left recursion , First figure out how to write production .

---

How to write production

One important rule to be clear about ： The production with high priority must be calculated first . So the higher the priority （ Such as multiplication and division ） Generative formula , stay BNF The closer to the leaf node in the tree . The lower the priority （ Such as addition and subtraction ） Generative formula , stay BNF The closer to the root node in the tree . Therefore, the production with low priority must be decomposed into the production with high priority .

in addition , In production The indecomposable element must be at the leaf node , Leaf node has no children , Cannot decompose .

Sum up ：

• BNF The working process of the algorithm is , First decompose down to the leaf node , Then follow the path of decomposition from the leaf node / Call stack up and down .
• Production priority and in BNF Is proportional to the depth in the tree .
• There are two kinds of leaf nodes , One is an indecomposable element , One is the element with the highest priority .

Take four operations as an example , Double brace () The highest priority , Multiplication and division */ The second priority is , Addition and subtraction operations have the lowest priority . From the following four operations BNF It can be seen that , An expression is first decomposed into ± operation , Then it is decomposed into multiplication and division */, Finally, it is decomposed into Expr, This shows that our understanding is correct .

<expr> ::= <expr> + <term>
         | <expr> - <term>
         | <term>

<term> ::= <term> * <factor>
         | <term> / <factor>
         | <factor>

<factor> ::= ( <expr> )
           | Num

According to the above thought , The following describes the writing process of production .

Four arithmetic expressions

ask ：

It is known that Expr The support is like 5+3 * (2+1) Operational expression of , That is, operation priority is supported , Multiplication and division are higher than addition and subtraction , Support subexpressions enclosed in parentheses . Seeking production .

answer ：

• 5 by Num,3 by Num,(2 + 1) Is a subexpression with parentheses (Expr)
• Num、(Expr) The highest priority , So make leaf nodes , Collectively, they are called Factor, namely
  Factor=Num | (Expr)

• The next highest priority operation is multiplication and division */, The expression is called Term, The basic operation element is from the previous step Factor, Yes
  • When the number of multiplication and division operators is 0 when ,Term = Factor
  • When the number of multiplication and division operators is 1 when ,Term = Factor * Factor | Factor / Factor, Let's put the above formula Term = Factor Brought in Term = Term * Factor | Term / Factor（ Left recursion ）.
  • When the number of multiplication and division operators is greater than 1 when ,
    Term = Factor * Factor / Factor …* Factor = (Factor * Factor / Factor…) * Factor =Term * Factor
    or
    Term = Factor * Factor / Factor…/ Factor = (Factor * Factor / Factor…) / Factor = Term / Factor.
    So the number of operators >= 1 when , Have the same production . In conclusion ：
    Term = Term * Factor | Term / Factor | Factor

• The lowest priority operation is addition and subtraction ±, The expression is called Expr, The basic operation element is from the previous step Term, Yes
  • When the number of addition and subtraction operators is 0 when ,Expr = Term
  • When the number of addition and subtraction operators is 1 when ,Expr = Term + Term | Term - Term, Substitute the above formula to get ,
    Expr = Expr + Term | Expr - Term
  • When the number of addition and subtraction operators is greater than 1 when ,Expr = Term + Term - Term…+ Term = (Term + Term - Term…) + Term = Expr + Term, or Expr = Term + Term - Term…- Term = (Term + Term - Term…) - Term = Expr - Term
    So the number of operators >= 1 when , Have the same production . In conclusion ：
    Expr = Expr + Term | Expr - Term | Term

---

Eliminate left recursion

Above we have derived the production formula of the four operations , But there is left recursion in production . Production with left recursion cannot be used to parse code , So we need to eliminate left recursion .
How to eliminate left recursion ？ As I said before , Use the non recursive part to represent the left recursive part . If there is no non recursive part , Left recursion cannot be eliminated . It is equivalent to a dead end , Take another detour . If there is no way to go , Is really no way to go .

Eliminate direct left recursion （ Ellipsis … It means to repeat for countless times ）：

Existing direct left recursion ：A = Aa | b,
namely A=A…a , Dexter A use b Replace , Equivalent to ： A = ba…a = ba…
Eliminates left recursion , That is to eliminate A =…a, only A = ba….
here A The production formula of is ：A = bAtail,Atail Except for the start symbol b The rest .
So what's the rest ？Atail = a…（ Right recursion ）, namely Atail = aAtail. Right recursion can be handled .
To sum up, the direct left recursion elimination method is ：
A = Aa | b => Eliminate left recursion => A = bA’, A’=aA’

thus it can be seen , The terminator is the bridge of transformation .

Eliminate indirect left recursion ：

The idea is to use variable substitution to write indirect left recursion into direct left recursion , Then eliminate direct left recursion . Please refer to this article for details ： The left recursive elimination of grammar analysis

coded

You can refer to this article ： Hands teach you how to make a C Language compiler （4）： Recursive descent

---

Last

What needs special explanation is ： The above is only in the case of known conclusions , An understanding of the conclusion . Be able to transform... From nothing BNF Create and perfect , It is by no means an easy thing .

---

​
Recently created a official account , Write articles regularly , Mainly Qt dependent . If you find the article useful , You can focus on that .