当前位置:网站首页>剑指Offer10- I. 斐波那契数列
剑指Offer10- I. 斐波那契数列
2022-07-03 11:50:00 【伍六琪】
剑指Offer10- I. 斐波那契数列
题目描述
写一个函数,输入 n ,求斐波那契(Fibonacci)数列的第 n 项(即 F(N))。斐波那契数列的定义如下:
F(0) = 0, F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.
斐波那契数列由 0 和 1 开始,之后的斐波那契数就是由之前的两数相加而得出。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
示例 1:
输入:n = 2
输出:1
示例 2:
输入:n = 5
输出:5
提示:
0 <= n <= 100
JAVA代码
一、递归方法(超出时间限制)
class Solution {
public int fib(int n) {
if(n0){
return 0;
}
if(n1){
return 1;
}
return fib(n-1)+fib(n-2);
}
}
二、数组辅助方法(动态规划dp)
class Solution {
public int fib(int n) {
final int MOD = 1000000007;
int[] result = new int[100000];
result[0] = 0;
result[1] = 1;
for(int i = 2;i<=n;i++){
result[i] = (result[i-1]+result[i-2])%MOD;
}
return result[n];
}
}

无需数组辅助方法(动态规划dp)
也可以像官方一样,不使用数组赋值,直接进行计算也是可以的。
class Solution {
public int fib(int n) {
final int MOD = 1000000007;
if(n==0||n==1) return n;
int num1 = 0,num2 =0,sum = 1;
for(int i = 2;i<=n;i++){
num1 = num2;
num2 = sum;
sum = (num1 + num2) % MOD;
}
return sum;
}
}

官方方法:矩阵快速幂
算法设计思想:

class Solution {
static final int MOD = 1000000007;
public int fib(int n) {
if (n < 2) {
return n;
}
int[][] q = {
{
1, 1}, {
1, 0}};
int[][] res = pow(q, n - 1);
return res[0][0];
}
//矩阵的n次幂乘
public int[][] pow(int[][] a, int n) {
//初始化为单位矩阵,存储计算结果
int[][] ret = {
{
1, 0}, {
0, 1}};
//偶数位我们直接计算a*a,这样就相当于规模减半
//有奇数位时,我们将提取保存好的res与奇数位相乘。->奇数位*偶数次幂乘
//这部分比较抽象,可以记住幂次相乘可以这样减少算法规模
while (n > 0) {
//判断是否为奇数 n%2==1
if ((n & 1) == 1) {
ret = multiply(ret, a);
}
//相当于n = n/2
n >>= 1;
a = multiply(a, a);
}
return ret;
}
//两个二维矩阵相乘方法
public int[][] multiply(int[][] a, int[][] b) {
//存放相乘后的结果
int[][] c = new int[2][2];
for (int i = 0; i < 2; i++) {
for (int j = 0; j < 2; j++) {
c[i][j] = (int) (((long) a[i][0] * b[0][j] + (long) a[i][1] * b[1][j]) % MOD);
}
}
return c;
}
}
时间复杂度O(logn),空间复杂度O(1)
总结:矩阵快速幂
矩阵快速幂:即矩阵的n次幂快速乘法
总结工具类:套用到任何一个矩阵的n次幂求解中
//矩阵的n次幂乘(n次幂相乘都可以套用这个思路)
public int[][] pow(int[][] a, int n) {
//初始化为单位矩阵,存储计算结果
int[][] ret = {
{
1, 0}, {
0, 1}};
//偶数位我们直接计算a*a,这样就相当于规模减半
//有奇数位时,我们将提取保存好的res与奇数位相乘。->奇数位*偶数次幂乘
//这部分比较抽象,可以记住幂次相乘可以这样减少算法规模
while (n > 0) {
//判断是否为奇数 n%2==1
if ((n & 1) == 1) {
ret = multiply(ret, a);
}
//相当于n = n/2
n >>= 1;
a = multiply(a, a);
}
return ret;
}
//两个二维矩阵相乘方法
public int[][] multiply(int[][] a, int[][] b) {
//存放相乘后的结果
int[][] c = new int[2][2];
for (int i = 0; i < 2; i++) {
for (int j = 0; j < 2; j++) {
c[i][j] = (int) (((long) a[i][0] * b[0][j] + (long) a[i][1] * b[1][j]) % MOD);
}
}
return c;
}
边栏推荐
- Atomic atomic operation
- init. RC service failed to start
- 347. Top k high frequency elements
- 2.7 overview of livedata knowledge points
- Flutter Widget : KeyedSubtree
- Dart: self study system
- Symlink(): solution to protocol error in PHP artisan storage:link on win10
- (construction notes) learning experience of MIT reading
- (构造笔记)从类、API、框架三个层面学习如何设计可复用软件实体的具体技术
- Fundamentals of concurrent programming (III)
猜你喜欢
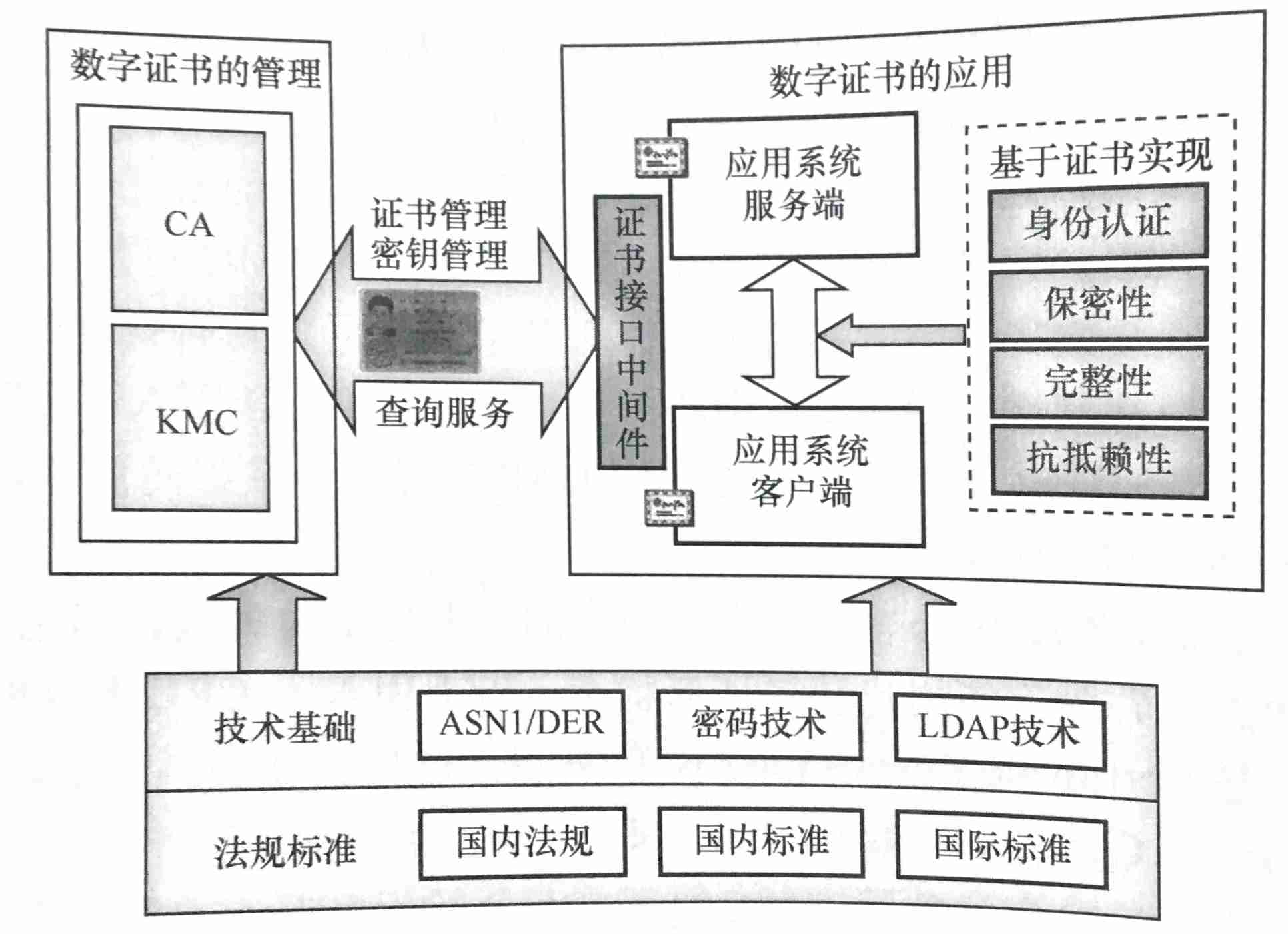
Pki/ca and digital certificate

Swagger

Summary of development issues

Cloud Computing future - native Cloud
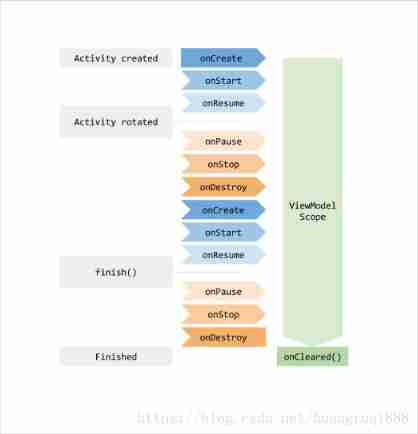
2.8 overview of ViewModel knowledge
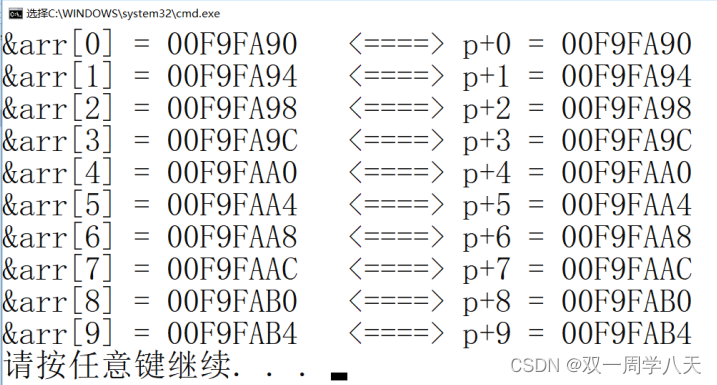
4000字超详解指针

(construction notes) ADT and OOP
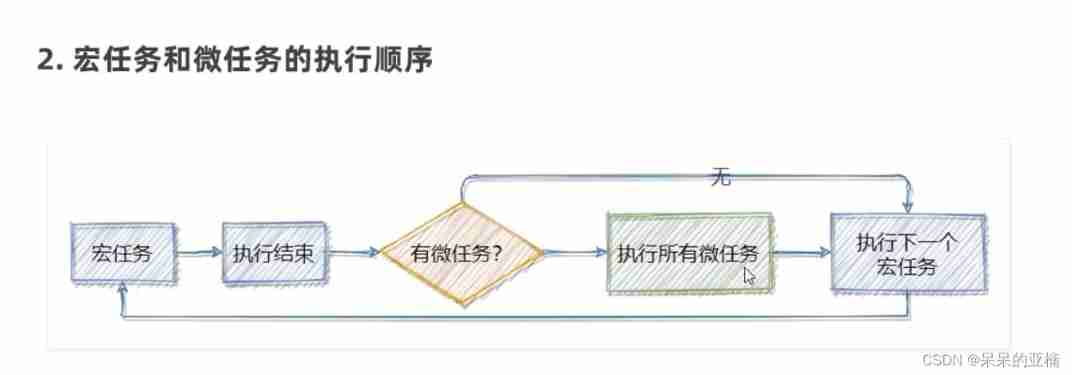
ES6 standard

What is more elegant for flutter to log out and confirm again?

Talk about the state management mechanism in Flink framework
随机推荐
win10 上PHP artisan storage:link 出现 symlink (): Protocol error的解决办法
Redis 笔记 01:入门篇
PHP get the file list and folder list under the folder
Optimize interface performance
Introduction to concurrent programming (II)
Summary of development issues
4000字超详解指针
云计算未来 — 云原生
Shell: basic learning
LeetCode 0556.下一个更大元素 III - 4步讲完
Php Export word method (One MHT)
网上炒股开户安不安全?谁给回答一下
Implement verification code verification
[combinatorics] permutation and combination (example of permutation and combination)
【嵌入式】---- 内存四区介绍
previous permutation lintcode51
257. All paths of binary tree
JVM memory model
20. Valid brackets
Display time with message interval of more than 1 minute in wechat applet discussion area