当前位置:网站首页>CF1705D Mark and Lightbulbs
CF1705D Mark and Lightbulbs
2022-08-01 22:42:00 【秦小咩】
Mark has just purchased a rack of nn lightbulbs. The state of the lightbulbs can be described with binary string s = s_1s_2\dots s_ns=s1s2…sn , where s_i=\texttt{1}si=1 means that the ii -th lightbulb is turned on, while s_i=\texttt{0}si=0 means that the ii -th lightbulb is turned off.
Unfortunately, the lightbulbs are broken, and the only operation he can perform to change the state of the lightbulbs is the following:
- Select an index ii from 2,3,\dots,n-12,3,…,n−1 such that s_{i-1}\ne s_{i+1}si−1=si+1 .
- Toggle s_isi . Namely, if s_isi is \texttt{0}0 , set s_isi to \texttt{1}1 or vice versa.
Mark wants the state of the lightbulbs to be another binary string tt . Help Mark determine the minimum number of operations to do so.
输入格式
The first line of the input contains a single integer qq ( 1\leq q\leq 10^41≤q≤104 ) — the number of test cases.
The first line of each test case contains a single integer nn ( 3\leq n\leq 2\cdot 10^53≤n≤2⋅105 ) — the number of lightbulbs.
The second line of each test case contains a binary string ss of length nn — the initial state of the lightbulbs.
The third line of each test case contains a binary string tt of length nn — the final state of the lightbulbs.
It is guaranteed that the sum of nn across all test cases does not exceed 2\cdot 10^52⋅105 .
输出格式
For each test case, print a line containing the minimum number of operations Mark needs to perform to transform ss to tt . If there is no such sequence of operations, print -1−1 .
输入输出样例
输入 #1复制
4 4 0100 0010 4 1010 0100 5 01001 00011 6 000101 010011
输出 #1复制
2 -1 -1 5
说明/提示
In the first test case, one sequence of operations that achieves the minimum number of operations is the following.
- Select i=3i=3 , changing \texttt{01}\color{red}{\texttt{0}}\texttt{0}0100 to \texttt{01}\color{red}{\texttt{1}}\texttt{0}0110 .
- Select i=2i=2 , changing \texttt{0}\color{red}{\texttt{1}}\texttt{10}0110 to \texttt{0}\color{red}{\texttt{0}}\texttt{10}0010 .
In the second test case, there is no sequence of operations because one cannot change the first digit or the last digit of ss .In the third test case, even though the first digits of ss and tt are the same and the last digits of ss and tt are the same, it can be shown that there is no sequence of operations that satisfies the condition.
In the fourth test case, one sequence that achieves the minimum number of operations is the following:
- Select i=3i=3 , changing \texttt{00}\color{red}{\texttt{0}}\texttt{101}000101 to \texttt{00}\color{red}{\texttt{1}}\texttt{101}001101 .
- Select i=2i=2 , changing \texttt{0}\color{red}{\texttt{0}}\texttt{1101}001101 to \texttt{0}\color{red}{\texttt{1}}\texttt{1101}011101 .
- Select i=4i=4 , changing \texttt{011}\color{red}{\texttt{1}}\texttt{01}011101 to \texttt{011}\color{red}{\texttt{0}}\texttt{01}011001 .
- Select i=5i=5 , changing \texttt{0110}\color{red}{\texttt{0}}\texttt{1}011001 to \texttt{0110}\color{red}{\texttt{1}}\texttt{1}011011 .
- Select i=3i=3 , changing \texttt{01}\color{red}{\texttt{1}}\texttt{011}011011 to \texttt{01}\color{red}{\texttt{0}}\texttt{011}010011 .
//非常精巧的一个题目,发现的规律是,一个置换无论进行多少次,都不会消灭一段0或者1,即s有多少段,t就有多少段。而且我们会发现,置换一次会将01分界线偏移一位,在排除无解(首位不同)的情况下,只需要求出每一个01分界点的坐标即可,在满足首位相同,01分界点个数相同的情况下,我们s,t的01段顺序就已经确保完全一致了,所以没有必要再去判断是否01段顺序不同
# include<iostream>
# include<deque>
using namespace std;
typedef long long int ll;
int a[200000+10],b[200000+10];
int main ()
{
int t;
cin>>t;
while(t--)
{
int n;
cin>>n;
string s,t;
cin>>s>>t;
if(s[0]!=t[0]||s[s.length()-1]!=t[t.length()-1])
{
cout<<-1<<'\n';
continue;
}
int len1=0,len2=0;
for(int i=1;i<n;i++)
{
if(s[i]!=s[i-1])
{
len1++;
a[len1]=i;
}
if(t[i]!=t[i-1])
{
len2++;
b[len2]=i;
}
}
if(len1!=len2)
{
cout<<-1<<'\n';
continue;
}
ll ans=0;
for(int i=1;i<=len1;i++)
{
ans+=abs(a[i]-b[i]);
}
cout<<ans<<endl;
}
return 0;
}边栏推荐
- 2022-08-01 第八组 曹雨 泛型 枚举
- 03. GO language variable definition, function
- 数据增强--学习笔记(图像类,cnn)
- [Niu Ke brush questions-SQL big factory interview questions] NO4. Travel scene (a taxi)
- 系统可用性:SRE口中的3个9,4个9...到底是个什么东西?
- 03、GO语言变量定义、函数
- 下载安装 vscode(含汉化、插件的推荐和安装)
- excel remove all carriage return from a cell
- 自建 Prometheus 采集腾讯云容器服务监控数据最佳实践
- 如何使用pywinauto和pyautogui将动漫小姐姐链接请回家
猜你喜欢
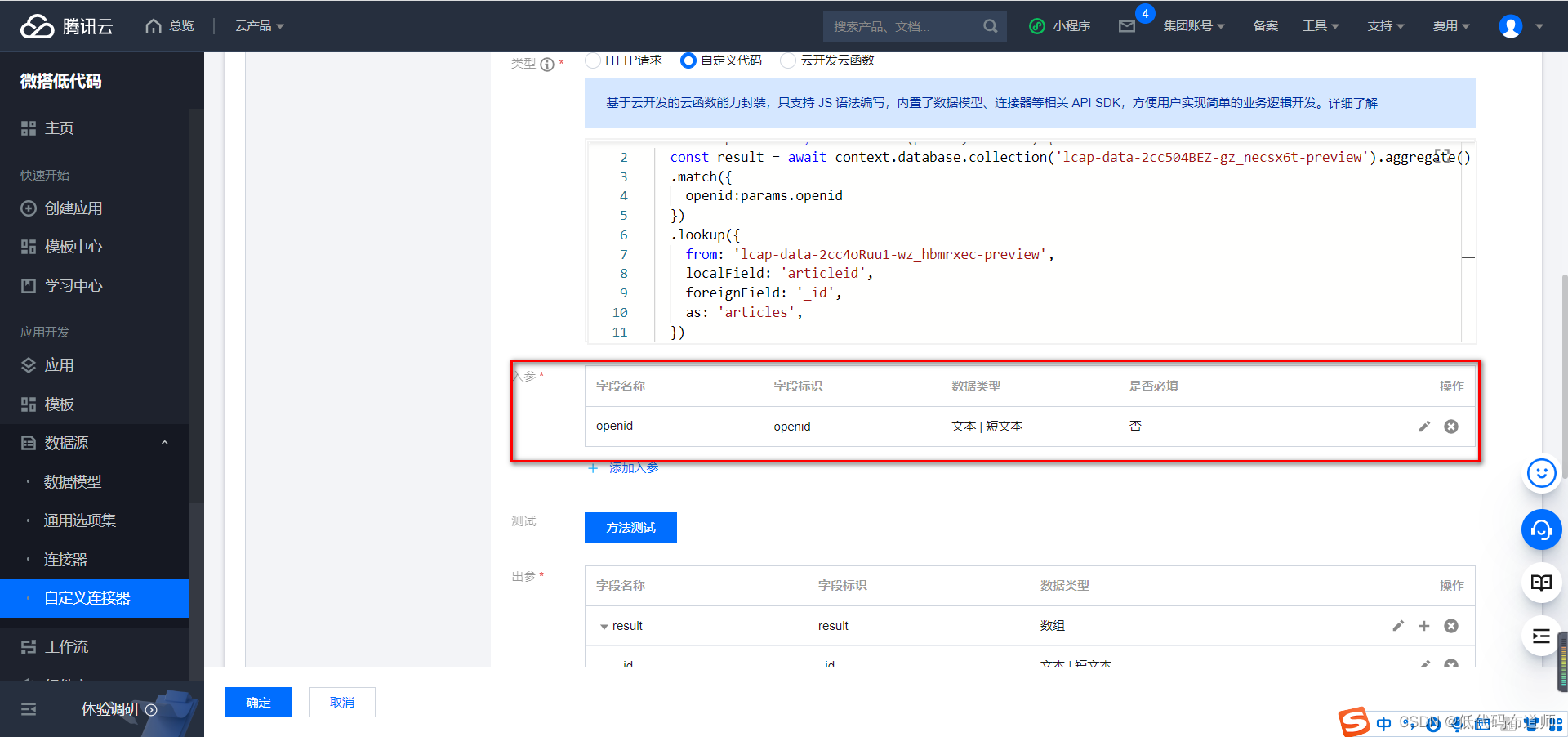
小程序中的多表联合查询

img 响应式图片的实现(含srcset属性、sizes属性的使用方法,设备像素比详解)

Prufer sequence
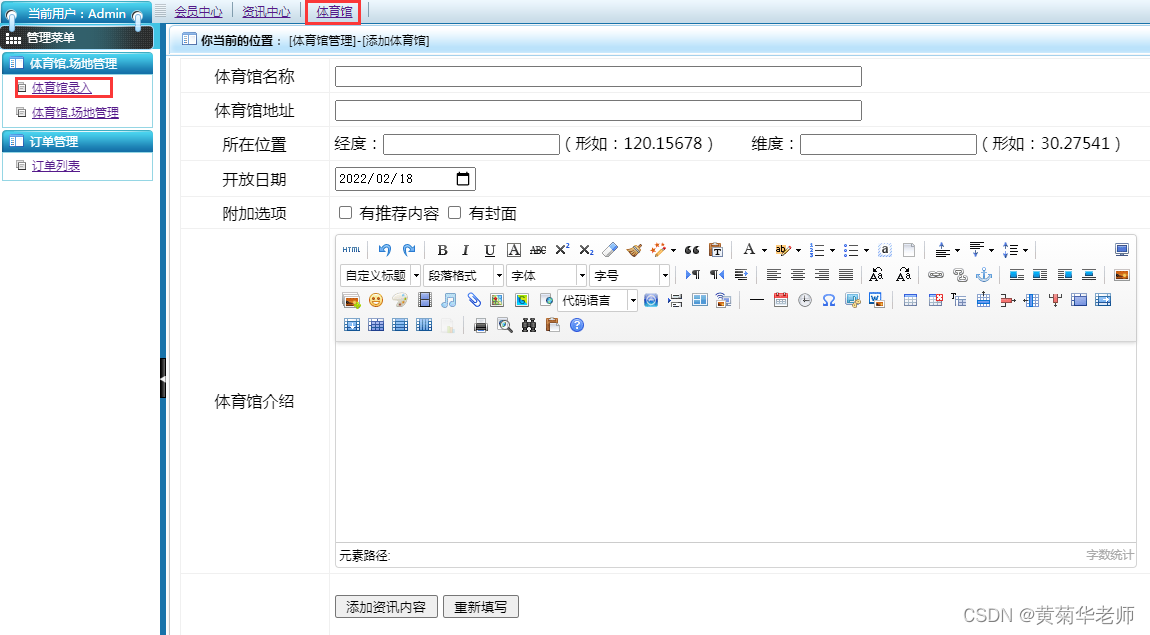
小程序毕设作品之微信体育馆预约小程序毕业设计成品(3)后台功能
![[深入研究4G/5G/6G专题-48]: 5G Link Adaption链路自适应-4-下行链路自适应DLLA-PDCCH信道](/img/6b/d4ff120493e878fcf5c9aa728eced7.png)
[深入研究4G/5G/6G专题-48]: 5G Link Adaption链路自适应-4-下行链路自适应DLLA-PDCCH信道

隔离和降级
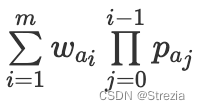
牛客多校4 A.Task Computing 思维
y84. Chapter 4 Prometheus Factory Monitoring System and Actual Combat -- Advanced Prometheus Alarm Mechanism (15)

SOM Network 2: Implementation of the Code

Advanced Algebra_Proof_The algebraic multiplicity of any eigenvalue of a matrix is greater than or equal to its geometric multiplicity
随机推荐
Prufer sequence
工程建筑行业数据中台指标分析
excel edit a cell without double clicking
feel so stupid
Codeforces CodeTON Round 2 (Div. 1 + Div. 2, Rated, Prizes!) A-D 题解
13、学习MySQL 分组
1391D. 505 状压dp
How to add a game character to a UE4 scene
NgRx Selector 的 Memoization 特性学习笔记
威纶通触摸屏如何打开并升级EB8000旧版本项目并更换触摸屏型号?
excel change cell size
隔离和降级
Implementation principle of VGUgarbage collector (garbage collector)
Wechat Gymnasium Reservation Mini Program Graduation Design Finished Work Mini Program Graduation Design Finished Product (2) Mini Program Function
三、mysql 存储引擎-建库建表操作
【Verilog刷题篇】硬件工程师从0到入门1|基础语法入门
Prufer序列
小程序毕设作品之微信美食菜谱小程序毕业设计成品(6)开题答辩PPT
线上故障排查方案
系统可用性:SRE口中的3个9,4个9...到底是个什么东西?