当前位置:网站首页>SOM Network 2: Implementation of the Code
SOM Network 2: Implementation of the Code
2022-08-01 21:48:00 【@BangBang】
SOMPrinciples of Self-Organizing Mapping Neural Networks,详见博客:SOM网络1:原理讲解
The main function for training
train_SO代码如下:
def train_SOM(X, # Output node row count
Y, # Number of output node columns
N_epoch, # epoch
datas, # 训练数据(N x D) N个D维样本
init_lr=0.5, # 初始化学习率 lr
sigma = 0.5, # 初始化 sigma Used to update domain node weights
dis_func = euclidean_distance, # 距离公式 Default Euler distance
neighborhood_func = gaussion_neighborhood, # Neighborhood node weight formulag Default Gaussian function
init_weight_fun=None, #初始化权重函数
seed=10):
# Get the feature dimension of the input
N,D =np.shape(datas)
# 训练的步数
N_steps =N_epoch*N
#对权重进行初始化
rng = np.random.RandomState(seed)
if init_weight_fun is None:
weights =rng.rand(X,Y,D)*2-1 #随机初始化
weights /=np.linalg.norm(weights,axis=-1,keepdims=True) #标准化
else:
weights = init_weight_fun(X,Y,datas) # 一般使用PCA初始化
PCA 初始化权重
def weights_PCA(X,Y,data):
N,D=np.shape(data)
weights=np.zeros([X,Y,D])
pc_value,pc=np.linalg.eig(np.conv(np.transpose(data))) # pc_vale为特征值,pc 为特征向量 DXD维
pc_order=np.argsort(-pc_value) # 特征值从大到小排序,并返回Index
# 对W:[X,Y,D]进行初始化
for i,c1 in enumerate(np.linspace(-1,1,X)):
for j,c2 in enumerate(np.linsapce(-1,1,Y)):
weights[i,j]=c1*pc[pc_order[0]]+c2*pc[pc_order[1]] #Take advantage of the biggest2The eigenvectors corresponding to the eigenvalues are weighted and combinedi,j位置的Ddimensional representation vector
完整的训练代码
def train_SOM(X, # Output node row count
Y, # Number of output node columns
N_epoch, # epoch
datas, # 训练数据(N x D) N个D维样本
init_lr=0.5, # 初始化学习率 lr
sigma = 0.5, # 初始化 sigma Used to update domain node weights
dis_func = euclidean_distance, # 距离公式 Default Euler distance
neighborhood_func = gaussion_neighborhood, # Neighborhood node weight formulag Default Gaussian function
init_weight_func=weights_PCA, #初始化权重函数
seed=10):
# Get the feature dimension of the input
N,D =np.shape(datas)
# 训练的步数
N_steps =N_epoch*N
#对权重进行初始化
rng = np.random.RandomState(seed)
if init_weight_func is None:
weights =rng.rand(X,Y,D)*2-1 #随机初始化
weights /=np.linalg.norm(weights,axis=-1,keepdims=True) #标准化
else:
weights = init_weight_fun(X,Y,datas) # 一般使用PCA初始化
for n_epoch in range(N_epoch):
print("Epoch %d" %(n_epoch+1))
#Shuffle the sample order
index=rng.permulation(np.arange(N))
for n_step,_id in enumerate(index):
# 取一个样本
x=datas[_id]
#计算learning rate (eta)
t=N*n_epoch + n_step
eta=get_learning_rate(init_lr,t,N_steps)
#Calculate the distance of each node of the sample distance output,and get the location of the activation point
winner=get_winner_index(x,weights,dis_func)
#根据激活点的位置计算临近点的权重 随着迭代的进行sigmaIt also needs to be continuously reduced
new_sigma=get_learning_rate(sigma,t,N_steps) # sigma The update is done in the same way as the learning rate
g=neighborhood_fun(X,Y,winner,new_sigma)
g=g*eta
#进行权重的更新
weights = weights + np.expand_dims(g,-1)*(x-weights)
# 打印量化误差
print("quantization_error=%.4f" %(get_quantization_error(data,weights)))
return weights
#计算学习率
def get_learning_rate(lr,t,max_steps): # t当前的steps max_steps=N x epoch (N样本数)
return lr/(1+t/(max_steps/2))
# 获取激活(winning points)节点的位置,与xThe output node position with the smallest distance
def get_winner_index(x,w,dis_func=euclidean_distance):
# 计算输入样本和各个节点的距离
dis = dis_func(x,w)
#找到距离最小的位置
index=np.where(dis ==np.min(dis))
return (index[0][0],index[1][0])
#利用高斯距离法计算临近点的权重
# X,Y模板大小,c中心点的位置
def gaussion_neighborhood(X,Y,c,sigma)
xx,yy=np.meshgrid(np.arange(X),np.arange(Y))
d=2*sigma*sigma
ax=np.exp(-np.power(xx-xx.T[c],2)/d)
ay=np.exp(-np.power(yy-yy.T[c],2)/d)
return (ax*ay).T
# 计算欧式距离
def euclidean_distance(x,w):
dis=np.expand_dims(x,axis=(0,1))-w # x:D w:[X,Y,D] Therefore, two dimensions need to be added x:D->x:[1,1,D]
return np.linalg.norm(dis,axis=-1) # 输出[X,Y] 二范数 is the Euler distance
# 特征标准化 (x-mu)/std
def feature_normalization(data):
mu=np.mean(data,axis=0,keepdims=True)
sigma=np.std(data,axis=0,keepdims=True)
return (data-mu)/sigma
def get_U_Matrix(weights):
X,Y,D=np.shape(weights)
um=na.nan * np.zeros((X,Y,8)) #8 领域
ii=[0 ,-1,-1,-1,0,1,1, 1]
jj=[-1,-1, 0, 1,1,1,0,-1]
for x in range(X):
for y in range(Y):
w_2=weights[x,y]
for k,(i,j) in enumerate(zip(ii,jj)):
if(x+i >=0 and x+i<X and y+j>=0 and y+j <Y):
w_1=weights[x+i,y+j]
um[x,y,k]=np.linalg.norm(w_1-w_2)
um=np.nansum(um,axis=2)
return um/um.max()
#计算量化误差 Calculate the average distance between each sample point and the mapped point
def get_quantization_error(data,weights):
w_x,w_y=zip(*[get_winner_index(d,weights) for d in datas])
error=datas-weights[w_x,w_y] # The distance to the cluster center of the data domain
error=np.linalg.norm(error,axis=-1)
return np.mean(error)
训练完成后,Returns the output node'sweights,维度为 [ X , Y , D ] [X,Y,D] [X,Y,D], Equivalent to solidifying the weights of the modelweights, weightsrepresents the current training sample.
测试
if __name__ == "__main__":
# seed 数据展示
columns=['area','perimeter','compactness','length_kernel','width_kernel',
'asymmetry_coefficient','length_kernel_groove','target']
data = pd.read_csv('seeds_dataset.txt',names=columns,sep='\t+',engine='python')
labs=data['target'].values
lab_names={
1:'Kama',2:'Rosa',3:'Canadian'}
datas=data[data.columns[:-1]].values
N,D=np.shape(datas)
print(N,D)
# 对训练数据进行标准化
datas = feature_normalization(datas)
#SOM的训练
weights=train_SOM()X=9,Y=9,N_epoch=2,datas=datas,sigma=1.5,init_weight_func=weights_PCA)
# 获取UMAP 用于可视化
UM=get_U_Matrix(weights)
plt.figure(figure=(9,9))
plt.pcolor(UM.T,cmap='bone_r') #plotting the distance map as background
plt.colorbar()
测试数据
U_Matrix
- The darker the color, the stronger the relationship with neighboring points,Stronger colors indicate less strong relationships with neighboring points.
Test the effect of classification
```python
if __name__ == "__main__":
# seed 数据展示
columns=['area','perimeter','compactness','length_kernel','width_kernel',
'asymmetry_coefficient','length_kernel_groove','target']
data = pd.read_csv('seeds_dataset.txt',names=columns,sep='\t+',engine='python')
labs=data['target'].values
lab_names={
1:'Kama',2:'Rosa',3:'Canadian'}
datas=data[data.columns[:-1]].values
N,D=np.shape(datas)
print(N,D)
# 对训练数据进行标准化
datas = feature_normalization(datas)
#SOM的训练
weights=train_SOM()X=9,Y=9,N_epoch=2,datas=datas,sigma=1.5,init_weight_func=weights_PCA)
# 获取UMAP 用于可视化
UM=get_U_Matrix(weights)
plt.figure(figure=(9,9))
plt.pcolor(UM.T,cmap='bone_r') #plotting the distance map as background
plt.colorbar()
# See the effect of classification
markers=['o','s','D']
colors =['C0','C1','C2']
for i in range(N):
x =datas[i]
w=get_winner_index(x,weights)
i_lab=labs[i]-1
plt.plot(w[0]+.5,w[1]+.5,markers[i_lab],markerfacecolor='None'
markeredgecolor=colors[i_lab],markersize=12,markeredgewidth=2)
plt.show()

边栏推荐
- 作业8.1 孤儿进程与僵尸进程
- Kubernetes第零篇:认识kubernetes
- ModuleNotFoundError: No module named 'yaml'
- Based on php Xiangxi tourism website management system acquisition (php graduation design)
- Port protocol for WEB penetration
- 求解多元多次方程解的个数
- shell specification and variables
- 熟悉的朋友
- scikit-learn no moudule named six
- Pytest: begin to use
猜你喜欢
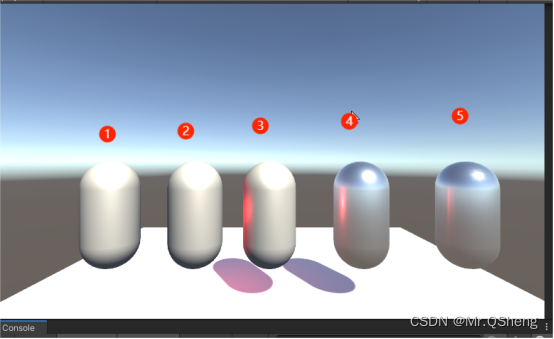
Unity Shader general lighting model code finishing
教你VSCode如何快速对齐代码、格式化代码
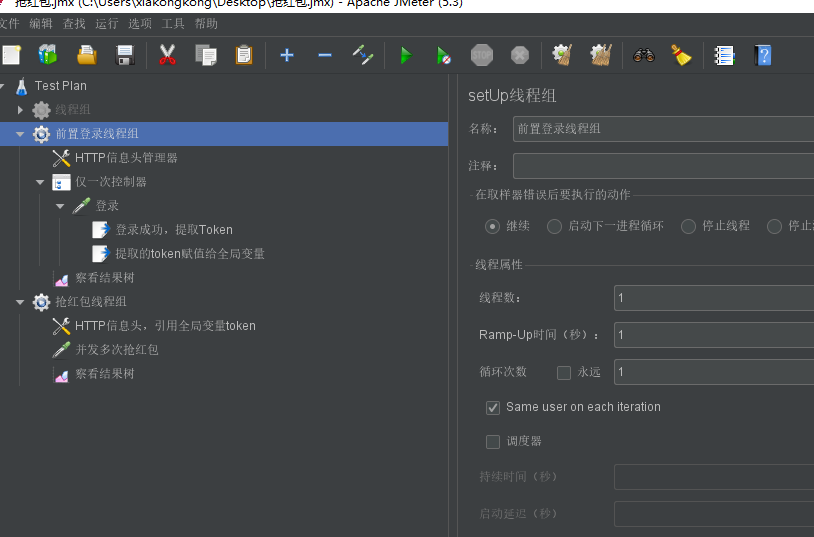
Jmeter combat | Repeated and concurrently grabbing red envelopes with the same user

Based on php hotel online reservation management system acquisition (php graduation project)

Based on php online learning platform management system acquisition (php graduation design)
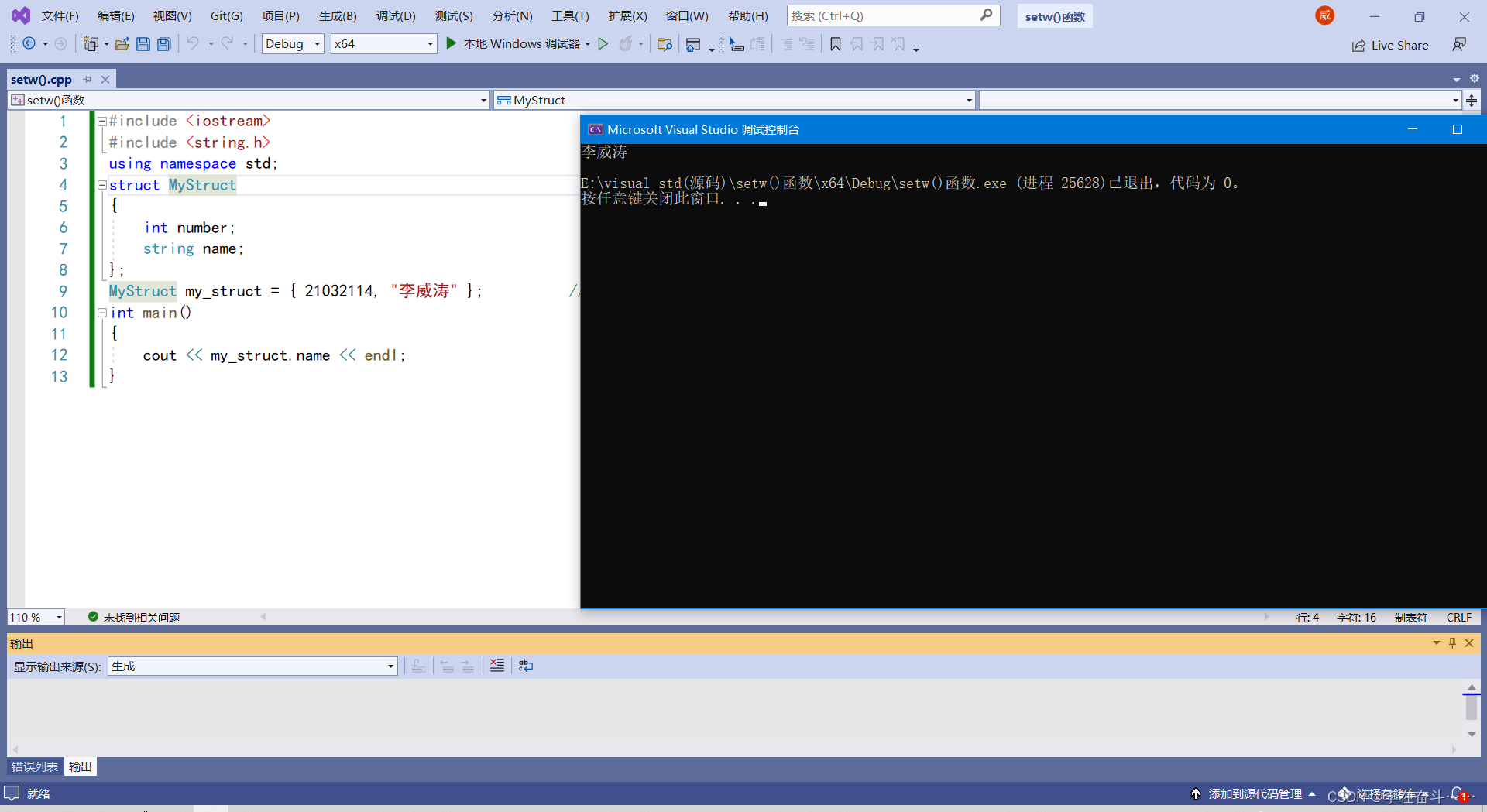
51.【结构体初始化的两种方法】
上传markdown文档到博客园

scikit-learn no moudule named six

SOM网络2: 代码的实现

Shell编程之条件语句
随机推荐
Kubernetes Scheduler全解析
如何防范 DAO 中的治理攻击?
SOM网络1:原理讲解
Transformer学习
入门数据库Days4
HCIP---企业网的架构
Shell编程之条件语句
File operations of WEB penetration
【C语言实现】最大公约数的3种求法
ModuleNotFoundError: No module named 'yaml'
树莓派的信息显示小屏幕,显示时间、IP地址、CPU信息、内存信息(c语言),四线的i2c通信,0.96寸oled屏幕
宝塔应用使用心得
LVS负载均衡群集
数据分析面试手册《指标篇》
Shell programming conditional statement
基于php影视资讯网站管理系统获取(php毕业设计)
恒星的正方形问题
网络水军第一课:手写自动弹幕
_ _ determinant of a matrix is higher algebra eigenvalue of the product, the characteristic value of matrix trace is combined
XSS漏洞