当前位置:网站首页>【C语言实现】最大公约数的3种求法
【C语言实现】最大公约数的3种求法
2022-08-01 21:34:00 【万羽西】
系列文章目录
C语言系列基础算法系列,每一篇博主都是努力做到用最多最优的解法实现,如果有想要了解的其他算法可以评论区留言哦!
整数排序的几种方法
两种平均成绩题型
求两个数的较大值
前言
最大公约数(gcd)是C语言学习过程中经常遇到的一种算法题,本篇博文将介绍求出两个数的最大公约数的各种解法。
提示:以下是本篇文章正文内容,下面案例可供参考
一、问题描述
求任意两个正整数的最大公约数(GCD)。
二、问题分析
如果有一个自然数 a 能被自然数 b 整除,则称 a 为 b 的倍数,b 为 a 的约数。几个自然数公有的约数,叫做这几个自然数的公约数。公约数中最大的一个公约数,称为这几个自然数的最大公约数。
根据约数的定义可知,某个数的所有约数必不大于这个数本身,几个自然数的最大公约数必不大于其中任何一个数。要求任意两个正整数的最大公约数即求出一个不大于其中两者中的任何一个,但又能同时整除两个整数的最大自然数
ps:
在我们求最大公约数的时候,要考虑两个数是否互质,如果互质,则没有最大公约数,所以我们在写代码的时候应该先判断两个是的互质情况。
问题解法
判断是否互质:
判断互质我们需要直到两点:
1.互质指最大公约数等于1的两个自然数。
2.1和任意数互质。
#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
// 如果是互质数返回0,不是则返回1
int is_coprime(int x, int y)
{
if (1 == x || 1 == y)
{
return 1;
}
int z = 0;
while (z = x % y)
{
if (0 == z)
{
break;
}
else
{
x = y;
y = z;
}
}
if (1 == y)
{
return 0;
}
else
{
return 1;
}
}
int main()
{
int a = 0;
int b = 0;
//输入
scanf("%d %d", &a, &b);
//判断是否为互质数
int ret = is_coprime(a, b);
return 0;
}
解法一:穷举法
因为公约数绝对不能超过两个自然数本身,所以第一思路应该是在两个数之间找到较小的那个,逐步自减一,直到找到一个能同时被两个自然数整除的公约数,就是最大公约数
#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
// 如果是互质数返回0,不是则返回1
int is_coprime(int x, int y)
{
if (1 == x || 1 == y)
{
return 0;
}
int z = 0;
while (z = x % y)
{
if (0 == z)
{
break;
}
else
{
x = y;
y = z;
}
}
if (1 == y)
{
return 0;
}
else
{
return 1;
}
}
int GCD1(int x, int y)
{
int tmp = 0;
//让x为较小的数
if (x > y)
{
//交换x,y的值
tmp = x;
x = y;
y = tmp;
}
int i = 0;
//从大到小找到符合条件的数
for (i = x; i > 0; i--)
{
if (0 == (x % i) && 0 == (y % i))
{
break;
}
}
return i;
}
int main()
{
int a = 0;
int b = 0;
int gcd = 0;
//输入
scanf("%d %d", &a, &b);
//判断是否为互质数
int ret = is_coprime(a, b);
if (ret)
{
gcd = GCD1(a, b);
}
printf("最大公约数为:%d\n", gcd);
return 0;
}
后文解法单独给出函数代码,互质数及主函数可与解法一相同
解法二:辗转相除法
图示:
代码:
int GCD2(int x, int y)
{
int z = 0;
while (z = x % y)
{
x = y;
y = z;
}
return y;
}
解法三:辗转相减法
图示:
代码:
int GCD3(int x, int y)
{
//两个数一直相减直到相等
while (x != y)
{
if (x > y)
{
x -= y;
}
else
{
y -= x;
}
}
return x;
}
总结
以上为三种求最大公约数的方法,希望能够给大家带来帮助
有想要整理的内容欢迎各位评论区留言嗷!
边栏推荐
猜你喜欢
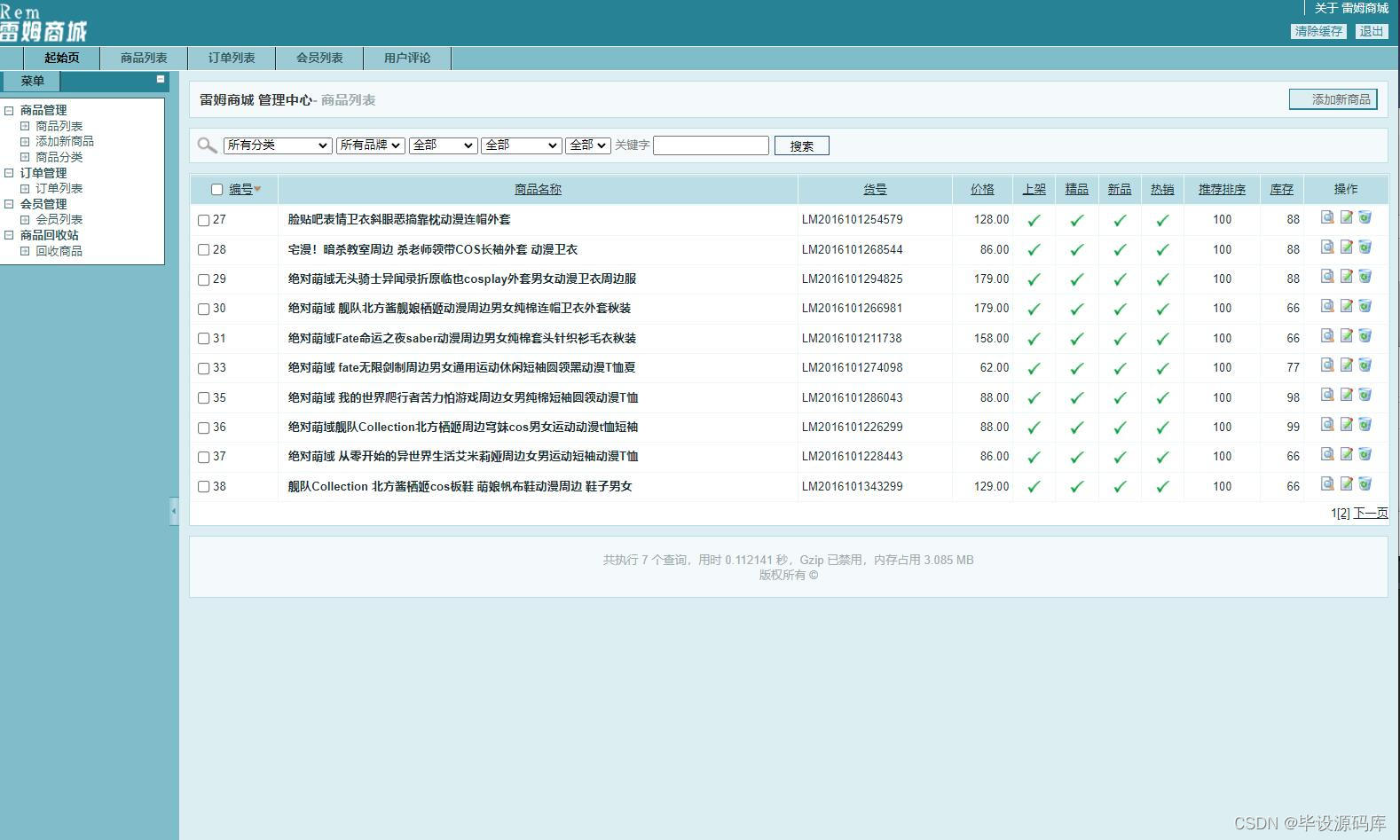
Based on php animation peripheral mall management system (php graduation design)

牛血清白蛋白刺槐豆胶壳聚糖缓释纳米微球/多西紫杉醇的纳米微球DTX-DHA-BSA-NPs

C语言_枚举类型介绍

365天挑战LeetCode1000题——Day 046 生成每种字符都是奇数个的字符串 + 两数相加 + 有效的括号
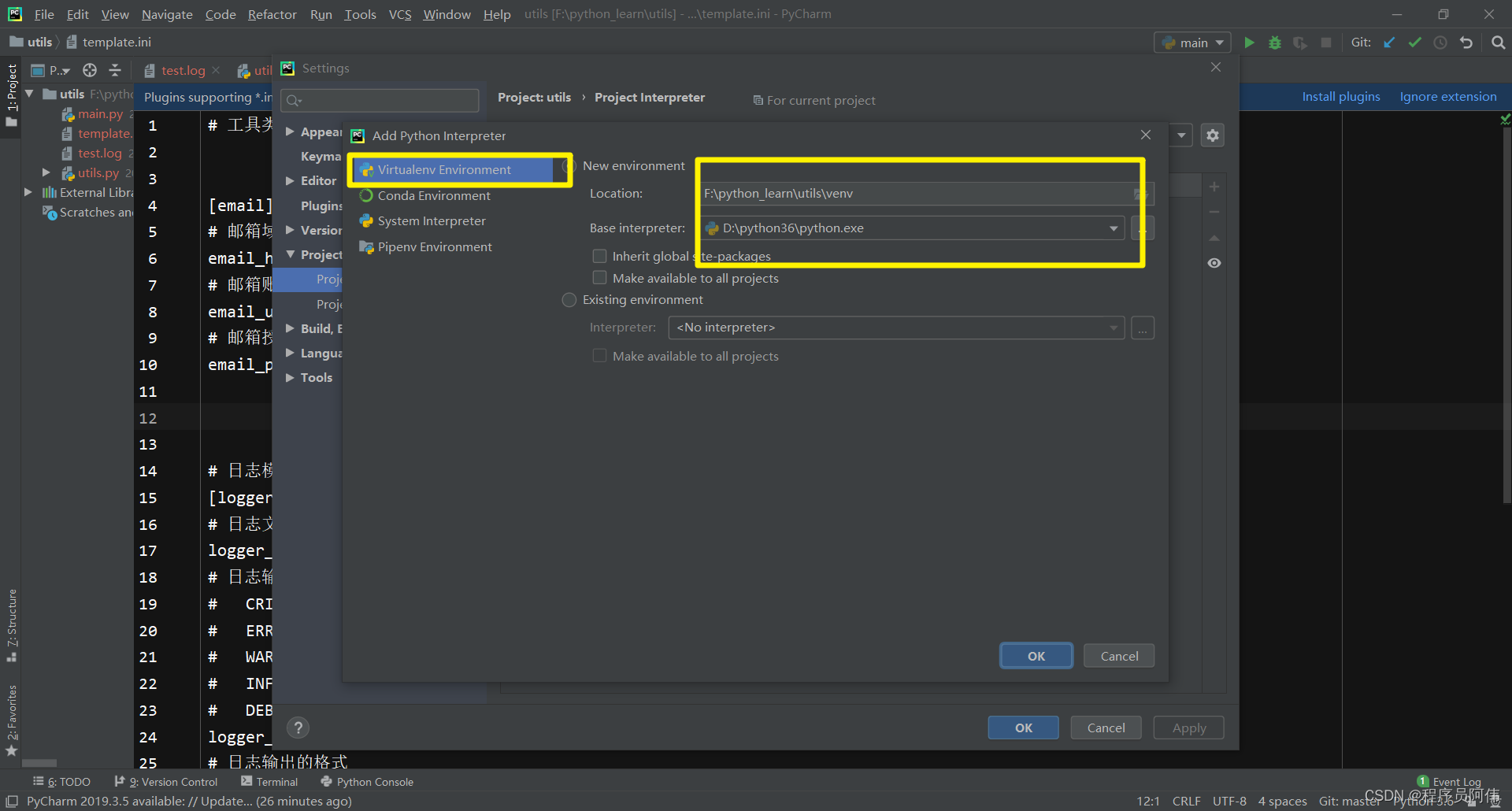
Uses of Anacoda
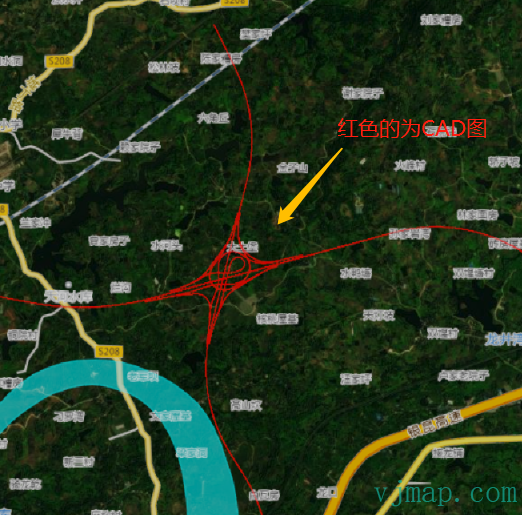
Realize the superposition display analysis of DWG drawing with CAD in Cesium

树莓派的信息显示小屏幕,显示时间、IP地址、CPU信息、内存信息(c语言),四线的i2c通信,0.96寸oled屏幕

方舟生存进化是什么游戏?好不好玩

365 days challenge LeetCode1000 questions - Day 046 Generate a string with odd number of each character + add two numbers + valid parentheses

Based on php Xiangxi tourism website management system acquisition (php graduation design)
随机推荐
你居然不懂Bitmap和Drawable? 相关知识大扫盲
可视化——Superset使用
ARFoundation Getting Started Tutorial U2-AR Scene Screenshot Screenshot
图像融合GANMcC学习笔记
多商户商城系统功能拆解19讲-平台端发票管理
HCIP---企业网的架构
Transformer学习
How to choose Visibility, Display, and Opacity when interacting or animating
模拟数据之mockjs
方舟:生存进化官服和私服区别
二分法中等 LeetCode6133. 分组的最大数量
C Expert Programming Chapter 1 C: Through the Fog of Time and Space 1.2 Early Experience of C Language
ImportError: `save_weights` requires h5py.问题解决
方舟生存进化是什么游戏?好不好玩
MySQL related knowledge
”sed“ shell脚本三剑客
C语言_联合体共用体引入
C Expert Programming Preface
一个关于操作数据库的建议—用户密码
shell specification and variables