当前位置：网站首页>Path Prefixes （倍增！树上の二分）

Path Prefixes （倍增！树上の二分）

2022-08-03 08:11:00 【lovesickman】

Path Prefixes （倍增！树上の二分）

题目描述

You are given a rooted tree. It contains $ n $ vertices, which are numbered from $ 1 $ to $ n $ . The root is the vertex $ 1 $ .

Each edge has two positive integer values. Thus, two positive integers $ a_j $ and $ b_j $ are given for each edge.

Output $ n-1 $ numbers $ r_2, r_3, \dots, r_n $ , where $ r_i $ is defined as follows.

Consider the path from the root (vertex $ 1 $ ) to $ i $ ( $ 2 \le i \le n $ ). Let the sum of the costs of $ a_j $ along this path be $ A_i $ . Then $ r_i $ is equal to the length of the maximum prefix of this path such that the sum of $ b_j $ along this prefix does not exceed $ A_i $ .

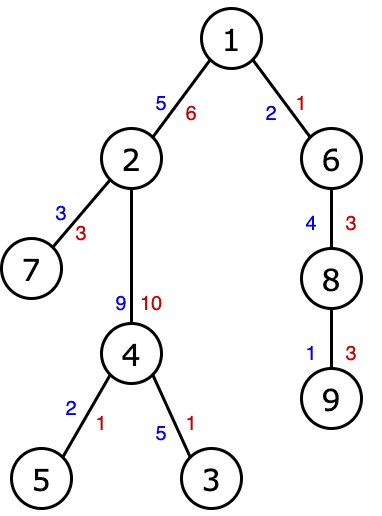Example for $ n=9 $ . The blue color shows the costs of $ a_j $ , and the red color shows the costs of $ b_j $ .Consider an example. In this case:

  • $ r_2=0 $ , since the path to $ 2 $ has an amount of $ a_j $ equal to $ 5 $ , only the prefix of this path of length $ 0 $ has a smaller or equal amount of $ b_j $ ;
  • $ r_3=3 $ , since the path to $ 3 $ has an amount of $ a_j $ equal to $ 5+9+5=19 $ , the prefix of length $ 3 $ of this path has a sum of $ b_j $ equal to $ 6+10+1=17 $ ( the number is $ 17 \le 19 $ );
  • $ r_4=1 $ , since the path to $ 4 $ has an amount of $ a_j $ equal to $ 5+9=14 $ , the prefix of length $ 1 $ of this path has an amount of $ b_j $ equal to $ 6 $ (this is the longest suitable prefix, since the prefix of length $ 2 $ already has an amount of $ b_j $ equal to $ 6+10=16 $ , which is more than $ 14 $ );
  • $ r_5=2 $ , since the path to $ 5 $ has an amount of $ a_j $ equal to $ 5+9+2=16 $ , the prefix of length $ 2 $ of this path has a sum of $ b_j $ equal to $ 6+10=16 $ (this is the longest suitable prefix, since the prefix of length $ 3 $ already has an amount of $ b_j $ equal to $ 6+10+1=17 $ , what is more than $ 16 $ );
  • $ r_6=1 $ , since the path up to $ 6 $ has an amount of $ a_j $ equal to $ 2 $ , the prefix of length $ 1 $ of this path has an amount of $ b_j $ equal to $ 1 $ ;
  • $ r_7=1 $ , since the path to $ 7 $ has an amount of $ a_j $ equal to $ 5+3=8 $ , the prefix of length $ 1 $ of this path has an amount of $ b_j $ equal to $ 6 $ (this is the longest suitable prefix, since the prefix of length $ 2 $ already has an amount of $ b_j $ equal to $ 6+3=9 $ , which is more than $ 8 $ );
  • $ r_8=2 $ , since the path up to $ 8 $ has an amount of $ a_j $ equal to $ 2+4=6 $ , the prefix of length $ 2 $ of this path has an amount of $ b_j $ equal to $ 1+3=4 $ ;
  • $ r_9=3 $ , since the path to $ 9 $ has an amount of $ a_j $ equal to $ 2+4+1=7 $ , the prefix of length $ 3 $ of this path has a sum of $ b_j $ equal to $ 1+3+3=7 $ .

输入格式

The first line contains an integer $ t $ ( $ 1 \le t \le 10^4 $ ) — the number of test cases in the test.

The descriptions of test cases follow.

Each description begins with a line that contains an integer $ n $ ( $ 2 \le n \le 2\cdot10^5 $ ) — the number of vertices in the tree.

This is followed by $ n-1 $ string, each of which contains three numbers $ p_j, a_j, b_j $ ( $ 1 \le p_j \le n $ ; $ 1 \le a_j,b_j \le 10^9 $ ) — the ancestor of the vertex $ j $ , the first and second values an edge that leads from $ p_j $ to $ j $ . The value of $ j $ runs through all values from $ 2 $ to $ n $ inclusive. It is guaranteed that each set of input data has a correct hanged tree with a root at the vertex $ 1 $ .

It is guaranteed that the sum of $ n $ over all input test cases does not exceed $ 2\cdot10^5 $ .

输出格式

For each test case, output $ n-1 $ integer in one line: $ r_2, r_3, \dots, r_n $ .

样例 #1

样例输入 #1

4
9
1 5 6
4 5 1
2 9 10
4 2 1
1 2 1
2 3 3
6 4 3
8 1 3
4
1 1 100
2 1 1
3 101 1
4
1 100 1
2 1 1
3 1 101
10
1 1 4
2 3 5
2 5 1
3 4 3
3 1 5
5 3 5
5 2 1
1 3 2
6 2 1

样例输出 #1

0 3 1 2 1 1 2 3 
0 0 3 
1 2 2 
0 1 2 1 1 2 2 1 1

提示

The first example is parsed in the statement.

In the second example:

  • $ r_2=0 $ , since the path to $ 2 $ has an amount of $ a_j $ equal to $ 1 $ , only the prefix of this path of length $ 0 $ has a smaller or equal amount of $ b_j $ ;
  • $ r_3=0 $ , since the path to $ 3 $ has an amount of $ a_j $ equal to $ 1+1=2 $ , the prefix of length $ 1 $ of this path has an amount of $ b_j $ equal to $ 100 $ ( $ 100 > 2 $ );
  • $ r_4=3 $ , since the path to $ 4 $ has an amount of $ a_j $ equal to $ 1+1+101=103 $ , the prefix of length $ 3 $ of this path has an amount of $ b_j $ equal to $ 102 $ , .

这是我的第一道树上倍增。还是dfs倍增好用

预处理 f a [ u ] [ i ] , g [ u ] [ i ] fa[u][i],g[u][i] fa[u][i],g[u][i] , g [ u ] [ i ] g[u][i] g[u][i] 表示从 u 节点开始向上跳跃 2 i 2^i 2i 层，从 u 到 f a [ u ] [ i ] fa[u][i] fa[u][i] 这条路径的 b b b 数组权值和。

深度随便开大点就行。

/* A: 10min B: 20min C: 30min D: 40min */ 
#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <cstring>
#include <queue>
#include <set>
#include <map>
#include <vector>
#include <sstream>
#define pb push_back 
#define all(x) (x).begin(),(x).end()
#define mem(f, x) memset(f,x,sizeof(f)) 
#define fo(i,a,n) for(int i=(a);i<=(n);++i)
#define fo_(i,a,n) for(int i=(a);i<(n);++i)
#define debug(x) cout<<#x<<":"<<x<<endl;
#define endl '\n'
using namespace std;
//#pragma GCC optimize("Ofast,no-stack-protector,unroll-loops,fast-math,O3")
//#pragma GCC target("sse,sse2,sse3,ssse3,sse4,popcnt,abm,mmx,avx,tune=native")

template<typename T>
ostream& operator<<(ostream& os,const vector<T>&v){
    for(int i=0,j=0;i<v.size();i++,j++)if(j>=5){
    j=0;puts("");}else os<<v[i]<<" ";return os;}
template<typename T>
ostream& operator<<(ostream& os,const set<T>&v){
    for(auto c:v)os<<c<<" ";return os;}
template<typename T1,typename T2>
ostream& operator<<(ostream& os,const map<T1,T2>&v){
    for(auto c:v)os<<c.first<<" "<<c.second<<endl;return os;}
template<typename T>inline void rd(T &a) {
    
    char c = getchar(); T x = 0, f = 1; while (!isdigit(c)) {
    if (c == '-')f = -1; c = getchar();}
    while (isdigit(c)) {
    x = (x << 1) + (x << 3) + c - '0'; c = getchar();} a = f * x;
}

typedef pair<int,int>PII;
typedef pair<long,long>PLL;

typedef long long ll;
typedef unsigned long long ull; 
const int N=2e5+10,M=1e9+7;
ll n,m,_;
int h[N],ne[N*2],e[N*2],idx;
ll w1[N],w2[N];
ll sa[N],sb[N];
ll dist[N],ans[N];
int dep[N];
int fa[N][30];  // f[u][i] 表示从u节点向上跳跃2^i层的祖先是谁
ll g[N][30]; // 表示从u节点出发向上跳跃2^i祖先 w2距离和是多少
void add(int a,int b){
    
    e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}

void dfs(int u,int father){
     // dfs打表lca
	fa[u][0] = father;
	g[u][0] = w2[u];
	for(int i=1;i<=20;i++){
    
		fa[u][i] = fa[fa[u][i-1]][i-1];
		g[u][i] = g[fa[u][i-1]][i-1] + g[u][i-1];
	}
	for(int i=h[u];~i;i=ne[i]){
    
		int j=e[i];
		if(j==father)continue;
		dep[j] = dep[u] + 1;
		sa[j] = sa[u] + w1[j];
		sb[j] = sb[u] + w2[j];
		dfs(j,u);
	}
}

void solve(){
    
    cin>>n;
    mem(h,-1);
    fo(i,2,n){
    
        ll u,a,b;cin>>u>>a>>b;
        add(i,u),add(u,i);
        w1[i]=a;w2[i]=b;
    }
    
    dfs(1,-1);
    fo(i,2,n){
    
    	ll ans = dep[i];
    	int u = i;
    	if(sa[u]<sb[u]){
    

    		ll t = sb[u]-sa[u]; // 至少跳跃t
    		for(int j=20;j>=0;j--){
    
    			if(g[u][j]<=t){
    
    				t-=g[u][j];
    				u = fa[u][j];
    				ans -= (1<<j);
    			}
    		}
    		if(t>0)ans--;
    	}
    	cout<<ans<<" ";
    }
    cout<<endl;
}

int main(){
    
	cin>>_;
	while(_--){
    
		solve();
	}
	return 0;
}

还可以树上二分，找小于等于 x 的最大值。

/* A: 10min B: 20min C: 30min D: 40min */ 
#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <cstring>
#include <queue>
#include <set>
#include <map>
#include <vector>
#include <sstream>
#define pb push_back 
#define all(x) (x).begin(),(x).end()
#define mem(f, x) memset(f,x,sizeof(f)) 
#define fo(i,a,n) for(int i=(a);i<=(n);++i)
#define fo_(i,a,n) for(int i=(a);i<(n);++i)
#define debug(x) cout<<#x<<":"<<x<<endl;
#define endl '\n'
using namespace std;
//#pragma GCC optimize("Ofast,no-stack-protector,unroll-loops,fast-math,O3")
//#pragma GCC target("sse,sse2,sse3,ssse3,sse4,popcnt,abm,mmx,avx,tune=native")

template<typename T>
ostream& operator<<(ostream& os,const vector<T>&v){
    for(int i=0,j=0;i<v.size();i++,j++)if(j>=5){
    j=0;puts("");}else os<<v[i]<<" ";return os;}
template<typename T>
ostream& operator<<(ostream& os,const set<T>&v){
    for(auto c:v)os<<c<<" ";return os;}
template<typename T1,typename T2>
ostream& operator<<(ostream& os,const map<T1,T2>&v){
    for(auto c:v)os<<c.first<<" "<<c.second<<endl;return os;}
template<typename T>inline void rd(T &a) {
    
    char c = getchar(); T x = 0, f = 1; while (!isdigit(c)) {
    if (c == '-')f = -1; c = getchar();}
    while (isdigit(c)) {
    x = (x << 1) + (x << 3) + c - '0'; c = getchar();} a = f * x;
}

typedef pair<int,int>PII;
typedef pair<long,long>PLL;

typedef long long ll;
typedef unsigned long long ull; 
const int N=2e5+10,M=1e9+7;
ll n,m,_;
int h[N],ne[N*2],e[N*2],idx;
ll w1[N],w2[N];
ll S[N];
int ans[N];

void add(int a,int b){
    
    e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}

void dfs(int u,int father,int dep,ll suma){
     // dfs打表lca
	suma += w1[u];
	S[dep] = S[dep-1] + w2[u];
	ans[u] = upper_bound(S+1,S+dep+1,suma)-S-1;
	for(int i=h[u];~i;i=ne[i]){
    
		int j=e[i];
		if(j==father)continue;
		dfs(j,u,dep+1,suma);
	}
}

void solve(){
    
    cin>>n;
    mem(h,-1);
    fo(i,2,n){
    
        ll u,a,b;cin>>u>>a>>b;
        add(i,u),add(u,i);
        w1[i]=a;w2[i]=b;
    }
    dfs(1,-1,0,0);
    fo(i,2,n){
    
		cout<<ans[i]<<" ";
    }
    cout<<endl;
}

int main(){
    
	cin>>_;
	while(_--){
    
		solve();
	}
	return 0;
}
原网站

版权声明
本文为[lovesickman]所创，转载请带上原文链接，感谢
https://blog.csdn.net/hacker__man/article/details/126117309

边栏推荐

猜你喜欢

随机推荐