当前位置：网站首页>【论文笔记】一种基于启发式奖赏函数的分层强化学习方法

【论文笔记】一种基于启发式奖赏函数的分层强化学习方法

2022-08-03 08:08:00 【Ctrl+Alt+L】

注：此论文发表时间在2011年。

摘要

针对问题 $\rightarrow$ 强化学习“维数灾难”、训练过程慢
提出 $\rightarrow$ 一种基于启发式奖赏函数的分层强化学习方法
应用场景 $\rightarrow$ 俄罗斯方块
效果 $\rightarrow$ 在一定程度上解决“维数灾”问题，并具有很好的收敛速度

关键词

分层强化学习；
试错；
启发式奖赏函数；
俄罗斯方块；
“维数灾难”

0 引言

目前解决“维数灾”问题的主要思想是抽象和逼近，这些思想可以细化为以下4种方法：

状态聚类法；
有限策略空间搜索法；
值函数逼近法
分层强化学习方法；

分层强化学习：

常用的抽象技术有状态空间分解、时态抽象、状态抽象
降低状态空间的维数和规模 $\rightarrow$ 加快学习速度
时态抽象法是目前最为常用的一种分层技术，几乎所有的HRL都用到
经过分层之后，学习任务或局限于智能体当前所处的规模较小的空间，或局限于与底层细节无关的维数较低的高层空间
代表的成果主要有Option，MAXQ和HAM，Option和MAXQ算法已被广泛的应用
先前学者研究：

学者	工作	优缺点
Neville等人	将奖赏函数表示为状态特征的向量，并通过调整此向量的权重值将已学习的经验应用到相同的层次结构中
Schultink和Cavallo等人	以MAXQ为基础的EHQ算法	理论上达到分层最优，但是为给予证明

使用分层算法解决的两个问题：

子目标的寻找 $\rightarrow$ Agent过去获得的经验 $\rightarrow$ 两种：
（1）根据状态访问的频率统计特征寻找子目标。
$\longrightarrow$ 到达终点的路径上经常访问的点，也可能是访问频率最高的节点作为子目标。
$\longrightarrow$ 缺点是被认为子目标的周围位置/节点也有可能是经常访问的。
$\longrightarrow$ 改进：访问频率的落差变化率。
（2）利用状态转移图构造子目标
$\longrightarrow$ 划分由最近经验构成的局部状态转移图
$\longrightarrow$ 利用主体访问的历史图通过Max-Flow/Min-cut算法找到子目标
（3）状态聚类法
（4）图论中的划分算法寻找子目标
任务自动分层
Option和MAXQ都能很好地实现自动分层
强化学习的任务分层主要还是根据设计者的经验给出，如何实现自动发现子目标并实现自动分层仍是当前研究的热点。（2011）

1 相关理论

奖赏函数的构建可分为两种形式：

稀疏函数
$r_{t} = \begin{cases} &1,Good-states; \\ &-1,Bad-states; \\ &0, others; \end{cases}$
设计简单，大多数这样采用
在早期学习阶段，系统Ｑ值表均为空值或预设值
系统就需要花费大量的时间去寻找非空、有意义的Q值
密集函数
$r_{t} = f(o_{t},i_{t}),\forall o,i;$
$o_{t} \rightarrow t$ 时步学习系统内在的状态；
$i_{t} \rightarrow t$ 时步学习系统外界环境状态；
在设计时必须清楚状态-动作空间的全部情况，所以，密集函数设计起来相对比较困难，但密集奖赏函数学习值函数比稀疏奖赏函数更容易
奖赏函数设计评价
奖赏函数应能提供学习进步的信息，嵌入隐含知识，并把它表达为奖赏函数中的形式
在建立奖赏函数时，对传统的稀疏奖赏函数附加对中间状态的评价有效

2 基于启发式奖赏函数的分层强化学习算法

2.1 子任务的定义及最优策略

三种子任务定义的方法：

按照确定的策略给出子任务的定义 $\rightarrow$ 由程序员给出（或者将某些已经学习过的
部分分离出来作为子任务） $\rightarrow$ Option方法
按照非确定的有限状态控制器定义 $\rightarrow$ HAM
按照终止条件和局部奖赏函数定义每个子任务 $\rightarrow$ This paper

变量定义：

$M$ 被分解为任务集合： $\{ M_{0},M_{1},\cdots,M_{n} \}$ ，每个任务是 $M_{i}$ ；
$M_{i} = < T_{i}, A_{i}, R_{i} >$ ；
$T_{i} \rightarrow$ 任务集； $A_{i} \rightarrow$ 动作集； $R_{i} \rightarrow$ 奖赏函数；
任务在分层中可以写成： $\pi = \{ \pi_{1},\pi_{2},\cdots,\pi_{n} \}$
任务在分层中的最优策略是： $\pi^{\ast} = \{ \pi_{1}^{\ast} ,\pi_{2}^{\ast} ,\cdots,\pi_{n}^{\ast} \}$

2.2 子任务的特征提取及附加奖赏函数

强化学习智能体训练过程：
学习的初始阶段 $\rightarrow$ 性能突然提升阶段 $\rightarrow$ 逐渐收敛阶段
负奖励值可以促使智能体对位置环境的探索

定义1

【内容】 $M_{i}$ 表示任务 $M$ 中第 $i$ 个子任务， $M_{i}$ 的特征向量表示为 $T_{i}$ 。
$T_{i} = \{ t_{i1},t_{i2},\cdots,t_{ik} \}$
$\rightarrow$ 特征向量的表示，实际上是一个矩阵
$\rightarrow$ $t_{ik}$ 表示 $T_{i}$ 子任务的第 $k$ 个状态。

定义2

【内容】特征向量 $T_{i}$ 的特征值向量为 $N_{i}$ 。
$N_{i} = \{ n_{i1},n_{i2},\cdots,n_{ik} \}$
$\rightarrow$ $n_{ik}$ 表示 $t_{ik}$ 子任务对应的特征值。

定义3

状态的每个特征对学习效果的影响力都不相同 $\rightarrow$ 对特征向量进行加权
【内容】特征向量对应的权值表示为 $W_{i}$ ：
$W_{i} = \{ w_{i1},w_{i2},\cdots,w_{ik} \}$

$w_{ik}>0 \rightarrow$ 出现某特征时给予鼓励；
$w_{ik}<0 \rightarrow$ 对出现的特征给予惩罚；
$w_{ik}=0 \rightarrow$ 忽略此特征的影响；

定义4

【内容】启发式奖赏函数的附加函数 $F_{i}$ ：
$F_{i} = W_{i}^{T}N_{i} = w_{i1}\times n_{i1} + w_{i2}\times n_{i2} + \cdots w_{ik}\times n_{ik}$

$F_{i}>0 \rightarrow$ 启发式奖励
$F_{i}<0 \rightarrow$ 启发式惩罚

定义5

【内容】基于广义MDP模型的奖赏函数
$R_{i}^{\prime} = R_{i} + F_{i} = R_{i}+ w_{i1}\times n_{i1} + w_{i2}\times n_{i2} + \cdots w_{ik}\times n_{ik}$
$F_{i}$ 是有界函数
$R_{i}^{\prime}$ 有界是智能体收敛的必要条件

2.3 最优策略

论文图片1
在策略 $\pi^{\ast}$ 下的最优子函数：
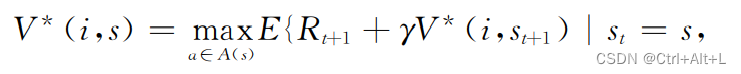
论文图片2-1
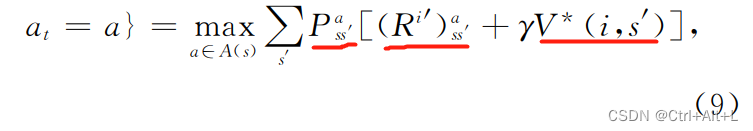
论文图片2-2
论文还定义了Q值和最优Q函数：
论文图片3

2.4 基于启发式奖赏函数的分层强化学习算法

存在任务 $\rightarrow$ 任务分解 $\rightarrow$ 初始化策略
$\rightarrow$ 抽取子任务的特征，得到特征向量和权值向量
$\rightarrow$ 智能体与环境交互
$\rightarrow$ 计算奖励函数和启发式奖赏函数 $\rightarrow$ Q值更新 $\rightarrow$ 进入下一状态

定理1

【内容】证明学习率收敛的定理：
论文图片4

定理2

【内容】分层算法只能收敛到递归最优
论文图片5
算法收敛到分层最优，当分层强化学习中的每一层的终止状态唯一时，递归最优将变为分层最优。

3 实验及结果分析

3.1 实验平台构成

名字	含义
Environment	俄罗斯方块的容器矩阵
State	左、右、顺时针旋转（最多四次）
Action	方块分布

$\rightarrow$ 其他特点和真实游戏相同
$\rightarrow$ 消行数作为游戏的得分

3.2 子任务特征提取及参数设置

论文图片6
论文图片7
贪心算法；
学习率 = 0.1；
折扣率 = 0.9；

3.3 结果及分析

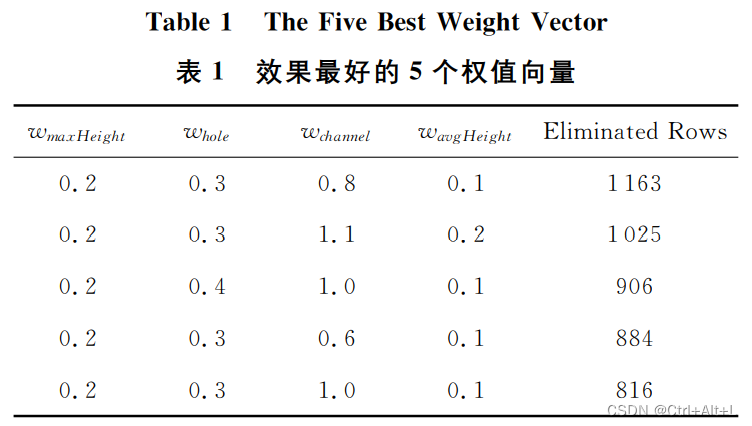
论文表格1

这篇论文没有给出与一般分层强化学习/Q学习的算法对比表现图。

$h o l e$ 和 $c hann e l$ 对实验结果的影响较大 $\rightarrow$ 过多，将会导致平台一直处于高位运行，那么局部最优更容易导致游戏结束
优于一般的分层算法和Q学习
只使用基本的强化学习算法 $\rightarrow$ 几乎不能得分
普通分层强化学习 $\rightarrow$ 部分解决“维数灾”问题，但实验的收敛速度较慢
游戏能同时满足在线实时的要求．即使在缺少先验知识和训练的前提下，依然能保持很好的性能