Gilbert Strang's course notes on linear algebra - Lesson 3

The topic of lesson 3 is ： Four understandings of matrix multiplication And Invertibility of matrix

---

Four understandings of matrix multiplication

Let's say I have a matrix AB = C

And A、B、C The three dimensions are ：m x p,p x n,m x n

1.  By definition , Set the objective matrix C Each element of is understood as Multiply rows by columns Result

Multiply according to the matrix in the previous document , Elements Cij originate ：A pass the civil examinations i Line with B pass the civil examinations j Column Multiply and get

 A pass the civil examinations i The elements of the row are ：ai1, ai2,... aip,B pass the civil examinations j The elements of the column are ：b1j,b2j,...Bpj

Cij = (A pass the civil examinations i That's ok ) * (B pass the civil examinations j Column ) = ai1*b1j + ai2*b2j...aip*bpj = Σaik*bkj (k∈1~p) To express

The shape change of this calculation process is ：

A Of the i The row shape is 1 x p,B Of the j The column shape is p x 1

1 x p,p x 1 => 1 x 1

So each group of rows and columns is multiplied , Will form a matrix C An element in , share m x n Group row and column , Composition matrix C in m x n Elements

2. Contrary to the definition , use Multiply columns by rows To understand from the perspective of

When we express matrix multiplication in terms of column and row multiplication , Look at the shape first ：

A pass the civil examinations i The shape of the column is ：m x 1,B pass the civil examinations j The shape of the row is ：1 x n

m x 1,1 x n => m x n, Just the size of the target matrix

So a set of columns and rows can be multiplied to get a m x n Matrix , The objective matrix consists of p The result of multiplying a group of columns by rows m x n Add the two matrices to get

For example, if it is difficult to understand ：

Multiply by the normal row and column to get ：

Multiply columns by rows to understand ：

3.  Explain according to the combination of rows and columns in lesson 2 —— Combination of columns

C pass the civil examinations i The column consists of a matrix A According to the matrix B pass the civil examinations i Column values （ matrix B The first i The value of the column indicates how to combine , First element b1i It means take b1i individual A The first column , The second element b2i It means take b2i individual A The second column of ... And so on ）

4.  Explain according to the combination of rows and columns in lesson 2 —— Combination of rows

C pass the civil examinations i The row consists of a matrix B According to the matrix A pass the civil examinations i Line values （ matrix A The first i The value of the row guides the combination , First element ai1 It means take ai1 individual B The first line of , The second element ai2 It means take ai2 individual B The second line of ... And so on ） 

---

  The quality of a matrix ： Support modular computing

 （ Each here A And B Does not represent a single element , It's a small matrix ）

（ The original course does not explain why this works , But it just works ）

---

Invertible properties of matrices

Definition ： When A-1A = I or AA-1 = I When established , We can say A It's reversible （invertible） And not strange （non-singular）

Definition supplement ：

Rank ： A matrix A The rank of is A The maximum number of linearly independent columns of . Similarly , Row rank is A The maximum number of linearly independent rows . The solution of rank is not expanded here

Singular matrix ： A square matrix with a non full rank is called a singular matrix

Nonsingular matrix ： A square matrix with full rank is called a nonsingular matrix

---

example ： Why singular matrices are irreversible ？

explain 1：

Suppose there is a singular matrix A（A There is a linear relationship between the first line and the second line in ）

For the sake of A The inverse matrix , We want to find a matrix E bring

Solve according to the row combination angle of the matrix E, We tried to put A In the second line of 2 Eliminate to... In the cell matrix on the right 0：

elimination 2 after , Right lower corner 1 It has also been eliminated , You can see that the current matrix cannot be transformed to the target matrix

explain A The inverse matrix of does not exist , matrix A Irreversible

explain 2：

Because of the singular matrix A There is a linear relationship between the first line and the second line in , We can find combinatorial relationships that make Ax = 0 establish （ This is related to the properties of singular matrices , Do not expand the principle for the time being ）

In this case ,3 The first column is related to -1 A second column can form 0 vector ：

 Ax = 0 establish , If we assume A reversible , Then multiply left and right Available

 , When we assume that A Reversible sometimes

Now the equation becomes Ix = 0, Solution , This is the same as that just worked out Contrary to each other , Description matrix A In this case it is irreversible ！

---

 

  example ： How to find the inverse matrix （Gauss-Jordan Method ）

Review first ： In the previous process of solving the ternary linear equations , We put

  In the form of a matrix

  For the sake of representation , hold A and b Write it after a matrix and eliminate it ：

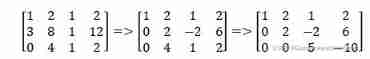
  So on this basis , Is there a form that is more conducive to problem solving ？

  If you change the matrix into The form of , You can get... Directly x = a,y = b,z =c！ 

So let's continue the transformation , Start to eliminate the upper and lower values of the fulcrum , Until the fulcrum is 1, The values outside the fulcrum are 0

  The four steps of the above process

step 1- Simplification ： The second line is divided by 2, Third line divided by 5, Change the fulcrum into 1

step 2- Elimination ： type 1-(2* type 2), take 1 That's ok 2 The value of the column is suppressed to 0

step 3- Elimination ： type 2+ type 3, take 2 That's ok 3 The value of the column is suppressed to 0

step 4- Elimination ： type 1-(3* type 3), take 1 That's ok 3 The value of the column is suppressed to 0

According to the last matrix, we can get ,x = 2,y = 1,z = -2

Now move this idea to ” Inverse matrix ” On the issue of ：

We know the formula , We will As an unknown matrix x, take I Set as the objective matrix b To look at

Apply the above method to solve

Suppose there is a square matrix

  According to the simplified method above A And b Spell it , Easy to eliminate

  Perform the elimination operation , Convert the left part into a cell matrix to solve ：

In the end, you get x Part of , namely  

That is to say A The inverse matrix ！

At the same time, we can look at this problem from another angle ：

The process can be viewed as After a certain transformation, it becomes （ Pretend you don't know what the matrix on the right of the result is , Set to M）

Use the whole transformation as E To express , namely

Then according to the property that the matrix can be modularized , Yes EA = I,EI = M

see EI = M： The matrix times the element matrix or is it itself , therefore E=M

see EA = I, According to the definition " When A-1A = I or AA-1 = I When established , We can say A Is reversible and nonsingular ", You know this E Namely A The inverse matrix ！