当前位置：网站首页>关于地图GIS开发事项的一次实践整理（上）
关于地图GIS开发事项的一次实践整理（上）
2022-08-02 23:31:00 【ZWZhangYu】
@
前言
在最近的一次开发事项中，需要根据第三方系统推送来数据在可视化地理图中进行展示。推送设备位置是固定的，数量不确定。推送来的消息有地理坐标。推送来的数据是整个大范围的数据，而我们需要进行划分匹配到对应的分类区域中。
一开始使用的方式是通过将设备位置和分类区域进行绑定，这个需要人工先进行数据的处理，把各个区域的设备记录下来，然后根据推送的数据进行映射匹配。这种方式是可行的，但是把各个区域所属的设备划分出来需要不少时间，而且有的区域自己也不清楚。
由于上面的方式比较粗暴耗时，在讨论过后又确认了使用来源事件坐标和区域范围进行判断，即将多个区域在地图中划分出来，划分出一个多边形区域标识，这个工作其实在之前已经完成了，有现成的数据，之后就是拿来源数据坐标去判断在那个多边形区域内。这样的设计相对来说更加灵活和简便。
其实这个事情本身并没有太多难点，但是用判断点在多边形的方式去处理地理区域位置判断，让自己有了更多的认识吧 【1】学会将问题进行抽象，发现问题的本质。 【2】遇到一些问题，学会尝试使用一些更加灵活更加合理的方式，而不是粗暴的去解决所有问题。 【3】对于一些地图GIS相关的代码应用，是否可以合理的使用一些几何算法去解决实际问题。 【4】在深入了解相关知识后，发现有很多的设计都可以运用几何的方式去解决问题。比如上班打卡定位就是二维平面中两点的距离；配送网点或者商家配送的范围就是一个圆形或者多边形的区域划分。 【5】此外，对于一些GIS的应用我们日常使用的中间件都或多或少的提供了一些API，这个都是之前不知道或者不曾留意的。比如MySQL就提供了GIS的一些函数和用于存储坐标的数据类型；Redis也提供了Gis的一些API应用，还有ElasticSearch、mongodb等等。 【6】不知道有没有和我一样的认知，坐标系是一个标准。在之前，我一直以为坐标系是一个标准，现在才知道原来各个平台的坐标系标准不一致，在使用特定的地理平台需要将当前坐标系转换为对应的坐标系标准。
考勤打卡和地图间两点距离计算
google地图距离算法 地图两点间距离算法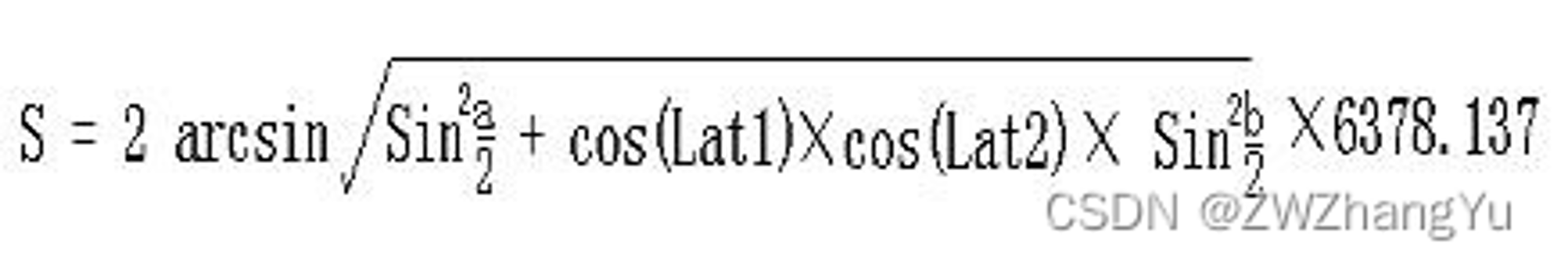 
对上面的公式解释如下： 【1】 Lat1表示A点经纬度， Lat2表示B点经纬度； 【2】a=Lat1 – Lat2 为两点纬度之差 b=Lng1 -Lng2 为两点经度之差； 【3】6378.137为地球半径，单位为千米； 【4】计算出来的结果单位为千米，若将半径改为米为单位则计算的结果单位为米。 【5】计算精度与谷歌地图的距离精度差不多，相差范围在0.2米以下。
public class Main {
/**
* 地球半径，单位千米
*/
private final static double EARTH_RADIUS = 6378.137;
/**
* 使用三角函数前，将角度转换为弧度
* 公式：弧度＝度×π/180
*
* @param degree 角度
* @return 弧度
*/
private static double getRadian(double degree) {
return degree * Math.PI / 180.0;
}
/**
* 依据经纬度计算两点之间的距离
*
* @param lat1 1点的纬度
* @param lng1 1点的经度
* @param lat2 2点的纬度
* @param lng2 2点的经度
* @return 距离 单位 米
*/
public static double getDistance(double lat1, double lng1, double lat2, double lng2) {
double radLat1 = getRadian(lat1);
double radLat2 = getRadian(lat2);
// 两点纬度差
double a = radLat1 - radLat2;
// 两点的经度差
double b = getRadian(lng1) - getRadian(lng2);
double s = 2 * Math.asin(Math.sqrt(Math.pow(Math.sin(a / 2), 2) + Math.cos(radLat1)
* Math.cos(radLat2) * Math.pow(Math.sin(b / 2), 2)));
s = s * EARTH_RADIUS;
return s * 1000;
}
public static void main(String[] args) {
// 117.139719,31.855583 合肥高新区置地中心
// 117.14397,31.852532 合肥高新区安医附院
System.out.println(getDistance(31.855583, 117.139719, 31.852532, 117.14397));
// 结果526.22米
}
考勤打卡
上面介绍了地图两点间距离算法，那么在实际一个应用比较适用就是上班考勤打卡，如下图所示，个人可以在距离企业点一定半径距离内进行打卡，而这就可以通过地图两点距离算法判断。在地图上也就是当前移动端设备的经纬度和企业经纬度的距离差。 
其实直接使用半径距离的方式在某些时候可能有些不足，比如在公司打卡位置正好有一个小区，如果划分半径的时候把这个包含了，那么在这个小区内在家就可以打卡考勤了，更加灵活的一个方式是划分特定的多边形区域，只有在自定义的区域内才可以实现打卡，而不是仅仅判断距离在中心点的半径范围内。
地理围栏服务和平面中如何判断点和平面的关系
场景介绍
地理围栏（Geo-fencing）是LBS的一种新应用，就是用一个虚拟的栅栏围出一个虚拟地理边界。在物流配送行业应用比较广，划分每个配送网点或者商家配送的范围，提高配送员的配送效率和服务的范围。
在地图中我们可能需要去判断在一个区域内是否存在某个坐标点，比如我判断一个人设备的坐标是否在某个城市范围内；在城市街道中，如果我想更加精确去推送给用户商铺产品信息，那么我可以将多个街道划分为多个虚拟地理区域，然后去实时跟踪用户设备坐标点，并根据用户所处的坐标点所在的地理区域进行更加精准的营销推送。
简单来看，就是在一个二维的平面中去判断一个点是否在某个多边形区域内。
使用JDK的awt.geom组件实现
Path2D类是java.awt.geom包提供的工具包，可表示任意几何路径的简单而灵活的形状。它可以完全表示PathIterator接口可以迭代的任何路径， 包括其所有段类型和绕组规则，并且它实现了Shape接口的所有基本命中测试方法。
使用Path2D.Float带有可表示且能使用浮点精度的数据的时候。使用Path2D.Double 对于需要双精度的准确性或范围的数据。
public static boolean isInPolygon(Point2D.Double point, List<Point2D.Double> polygon) {
GeneralPath generalPath = new GeneralPath();
//区域起始点
Point2D.Double first = polygon.get(0);
generalPath.moveTo(first.x, first.y);
polygon.remove(0);
//绘制范围
for (Point2D.Double d : polygon) {
generalPath.lineTo(d.x, d.y);
}
//回到起始点，封闭范围
generalPath.lineTo(first.x, first.y);
generalPath.closePath();
return generalPath.contains(point);
}
上面是一种参考的实现方式，其中主要API介绍如下： moveTo(double x, double y) 通过移动到以double精度指定的指定坐标，向路径添加一个点。 lineTo(double x, double y) 通过从当前坐标绘制直线到以double精度指定的新指定坐标，将路径添加到路径。 closePath() 通过将直线绘制回最后一个坐标来关闭当前子路径moveTo。 Path2D#contains判断一个点是否在绘制的图形范围内。
【测试】
import java.awt.geom.GeneralPath;
import java.awt.geom.Point2D;
import java.util.ArrayList;
import java.util.List;
/**
* 测试Point2D绘图
*
* @author zhangyu
**/
public class Test {
public static boolean isInPolygon(Point2D.Double point, List<Point2D.Double> polygon) {
GeneralPath generalPath = new GeneralPath();
//区域起始点
Point2D.Double first = polygon.get(0);
generalPath.moveTo(first.x, first.y);
polygon.remove(0);
//绘制范围
for (Point2D.Double d : polygon) {
generalPath.lineTo(d.x, d.y);
}
//回到起始点，封闭范围
generalPath.lineTo(first.x, first.y);
generalPath.closePath();
return generalPath.contains(point);
}
public static void main(String[] args) {
Point2D.Double a1 = new Point2D.Double(100, 0);
Point2D.Double a2 = new Point2D.Double(0, 100);
Point2D.Double a3 = new Point2D.Double(100, 100);
Point2D.Double a4 = new Point2D.Double(0, 0);
List<Point2D.Double> list = new ArrayList<>();
list.add(a1);
list.add(a2);
list.add(a3);
list.add(a4);
Point2D.Double point = new Point2D.Double(90, 50);
System.out.println(isInPolygon(point, list));
}
}
在执行上述代码后，结果为false，和我们的预期不一致。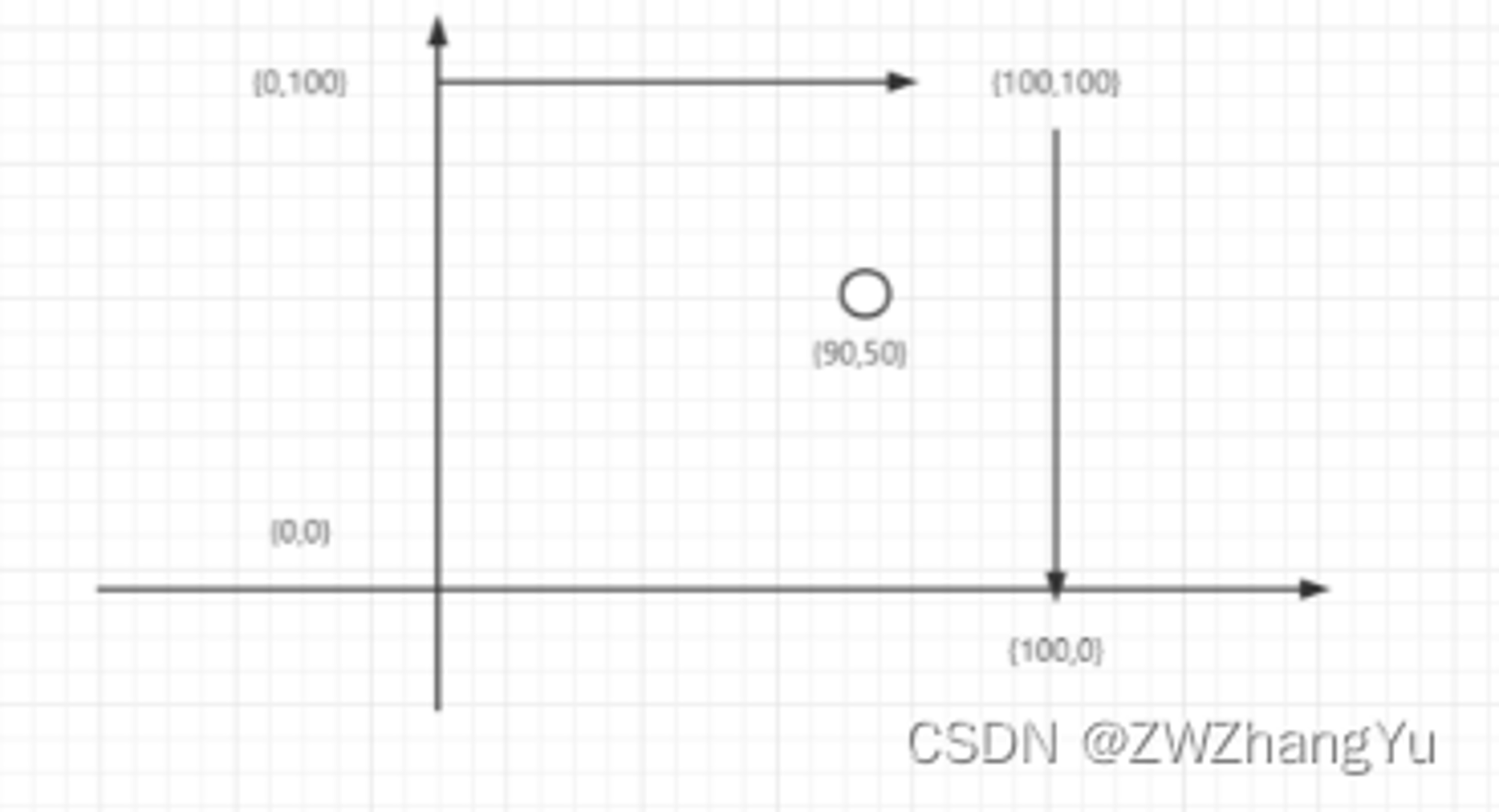 
上图应该是预期的图形，但是根据我们提供的数据数据，AWT绘制出来的样式是： 
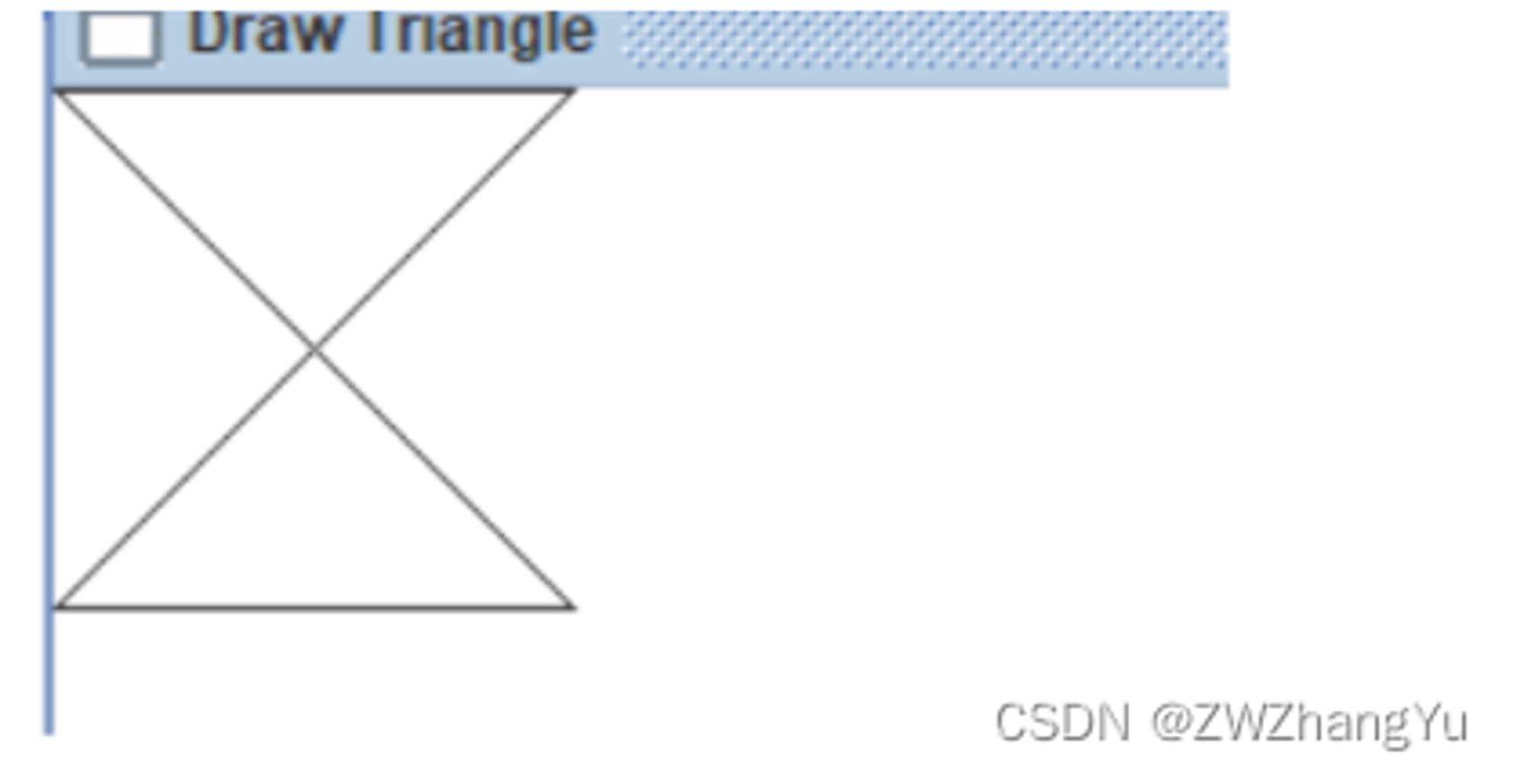绘制的结果如上图所示，这也就解释了为什么{90,50}为什么不在该多边形范围内，因为我们的连线顺序并不是按照边侧顺序来的，AWT绘制只知道根据点进行连线，结果就绘制出了上面的图形。 重要：如果选择了AWT包组件作为实现方式，那么一定要注意你的绘制顺序。
【修复数据再进行测试】 在调整数据顺序后，在进行测试可以发现已经和我们预期一样了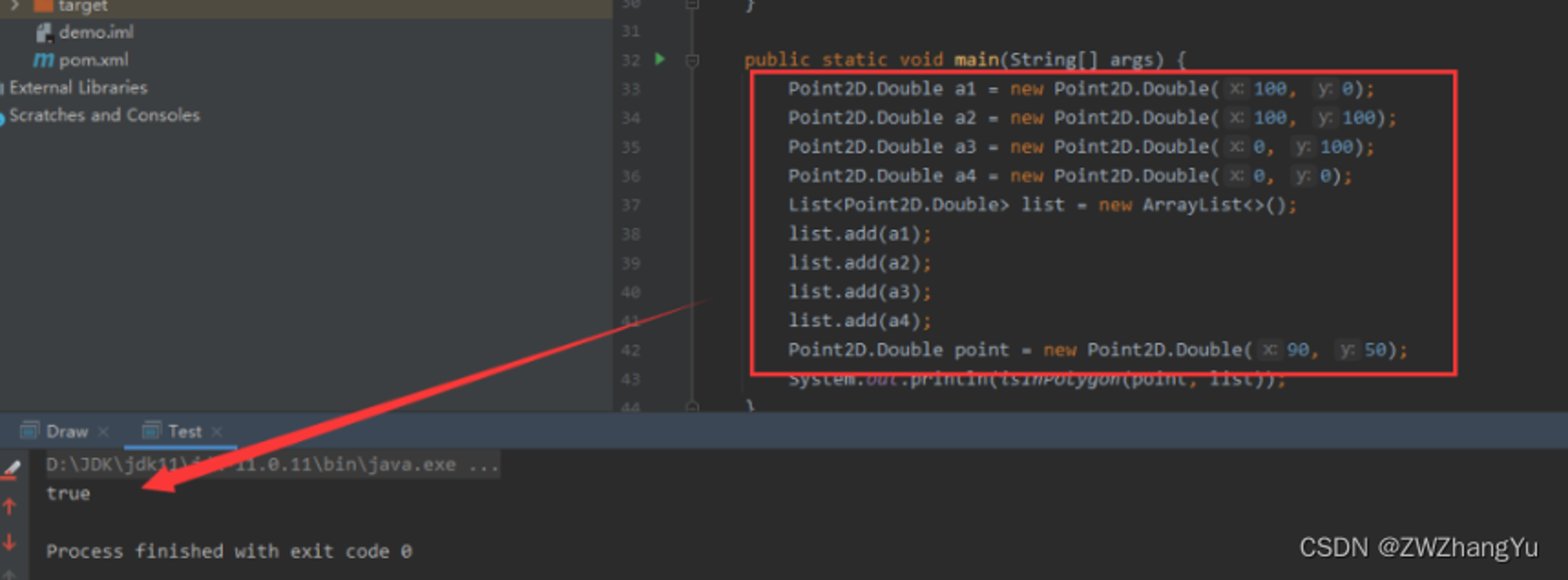 
绘制的图形如下，这个测试代码就不提供了，仅仅是为了更好的展示问题，无实际意义。 
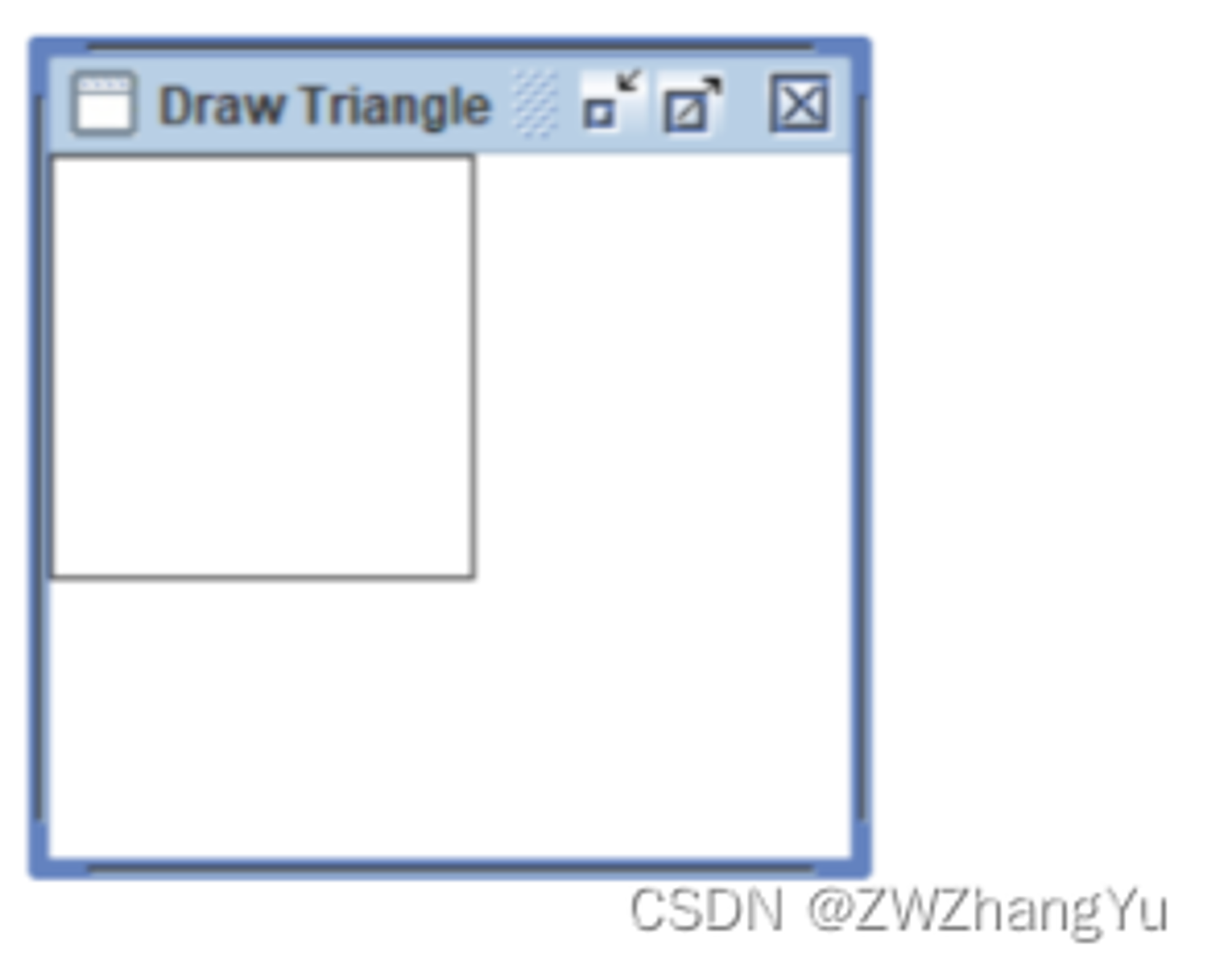检查给定点是否位于多边形内部或外部算法参考 解决这个问题的想法是基于判断两个给定的线段是否相交，并使用如下：
【1】在每个点的右侧画一条水平线并将其延伸到无穷大 【2】计算线与多边形边缘相交的次数。 【3】如果交点数为奇数或点位于多边形的边缘，则该点位于多边形内。如果没有一个条件为真，那么点就在外面。 【4】在多边形内，要根据实际情况考虑一些特殊情况，如点在多边形顶点上，点在多边形边上等特殊情况。
/**
* 检查给定点是否位于多边形内部或外部
*/
public class PointInPolygon {
static int INF = 10000;
static class Point {
int x;
int y;
public Point(int x, int y) {
this.x = x;
this.y = y;
}
}
static boolean onSegment(Point p, Point q, Point r) {
if (q.x <= Math.max(p.x, r.x) &&
q.x >= Math.min(p.x, r.x) &&
q.y <= Math.max(p.y, r.y) &&
q.y >= Math.min(p.y, r.y)) {
return true;
}
return false;
}
static int orientation(Point p, Point q, Point r) {
int val = (q.y - p.y) * (r.x - q.x)
- (q.x - p.x) * (r.y - q.y);
if (val == 0) {
return 0;
}
return (val > 0) ? 1 : 2;
}
static boolean doIntersect(Point p1, Point q1,
Point p2, Point q2) {
int o1 = orientation(p1, q1, p2);
int o2 = orientation(p1, q1, q2);
int o3 = orientation(p2, q2, p1);
int o4 = orientation(p2, q2, q1);
if (o1 != o2 && o3 != o4) {
return true;
}
if (o1 == 0 && onSegment(p1, p2, q1)) {
return true;
}
if (o2 == 0 && onSegment(p1, q2, q1)) {
return true;
}
if (o3 == 0 && onSegment(p2, p1, q2)) {
return true;
}
if (o4 == 0 && onSegment(p2, q1, q2)) {
return true;
}
return false;
}
static boolean isInside(Point polygon[], int n, Point p) {
if (n < 3) {
return false;
}
Point extreme = new Point(INF, p.y);
int decrease = 0;
int count = 0, i = 0;
do {
int next = (i + 1) % n;
if (polygon[i].y == p.y) decrease++;
if (doIntersect(polygon[i], polygon[next], p, extreme)) {
if (orientation(polygon[i], p, polygon[next]) == 0) {
return onSegment(polygon[i], p,
polygon[next]);
}
count++;
}
i = next;
} while (i != 0);
count -= decrease;
return (count % 2 == 1);
}
}
【测试】
public static void main(String[] args) {
Point polygon[] = {new Point(0, 0),
new Point(10, 0),
new Point(10, 10),
new Point(0, 10)};
int n = polygon.length;
Point p = new Point(10, 4);
if (isInside(polygon, n, p)) {
System.out.println("Yes");
} else {
System.out.println("No");
}
}
百度和高德几何计算工具类参考
日常工作中一般常用有百度和高德地图平台。在使用中也发现了其大都提供了一些几何计算的API工具，这里简单整理下，方便以后开发使用。
百度地图
百度地图JSAPI GL版JavaScript开源工具库 
主要的计算方法在GeoUtils.js中
/**
* @fileoverview GeoUtils类提供若干几何算法，用来帮助用户判断点与矩形、
* 圆形、多边形线、多边形面的关系,并提供计算折线长度和多边形的面积的公式。
* 主入口类是<a href="symbols/BMapGLLib.GeoUtils.html">GeoUtils</a>，
* 基于Baidu Map API GL 1.0。
*
* @author Baidu Map Api Group
* @version 1.0
*/
/**
* @namespace BMapGL的所有library类均放在BMapGLLib命名空间下
*/
var BMapGLLib = (window.BMapGLLib = BMapGLLib || {});
(function () {
/**
* 地球半径
*/
var EARTHRADIUS = 6370996.81;
/**
* @exports GeoUtils as BMapGLLib.GeoUtils
*/
var GeoUtils =
/**
* GeoUtils类，静态类，勿需实例化即可使用
* @class GeoUtils类的<b>入口</b>。
* 该类提供的都是静态方法，勿需实例化即可使用。
*/
(BMapGLLib.GeoUtils = function () {
});
/**
* 判断点是否在矩形内
* @param {Point} point 点对象
* @param {Bounds} bounds 矩形边界对象
* @returns {Boolean} 点在矩形内返回true,否则返回false
*/
GeoUtils.isPointInRect = function (point, bounds) {
//检查类型是否正确
if (
!(point.toString() === "Point" || point.toString() === "LatLng") ||
!(bounds instanceof BMapGL.Bounds)
) {
return false;
}
// 西南脚点
var sw = bounds.getSouthWest();
// 东北脚点
var ne = bounds.getNorthEast();
return (
point.lng >= sw.lng &&
point.lng <= ne.lng &&
point.lat >= sw.lat &&
point.lat <= ne.lat
);
};
/**
* 判断点是否在圆形内
* @param {Point} point 点对象
* @param {Circle} circle 圆形对象
* @returns {Boolean} 点在圆形内返回true,否则返回false
*/
GeoUtils.isPointInCircle = function (point, circle) {
//检查类型是否正确
if (
!(point.toString() === "Point" || point.toString() === "LatLng") ||
!(circle instanceof BMapGL.Circle)
) {
return false;
}
//point与圆心距离小于圆形半径，则点在圆内，否则在圆外
var c = circle.getCenter();
var r = circle.getRadius();
var dis = GeoUtils.getDistance(point, c);
if (dis <= r) {
return true;
} else {
return false;
}
};
/**
* 判断点是否在折线上
* @param {Point} point 点对象
* @param {Polyline} polyline 折线对象
* @returns {Boolean} 点在折线上返回true,否则返回false
*/
GeoUtils.isPointOnPolyline = function (point, polyline) {
//检查类型
if (
!(point.toString() === "Point" || point.toString() === "LatLng") ||
!(polyline instanceof BMapGL.Polyline)
) {
return false;
}
//首先判断点是否在线的外包矩形内，如果在，则进一步判断，否则返回false
var lineBounds = polyline.getBounds();
if (!this.isPointInRect(point, lineBounds)) {
return false;
}
//判断点是否在线段上，设点为Q，线段为P1P2 ，
//判断点Q在该线段上的依据是：( Q - P1 ) × ( P2 - P1 ) = 0，且 Q 在以 P1，P2为对角顶点的矩形内
var pts = polyline.getPath();
for (var i = 0; i < pts.length - 1; i++) {
var curPt = pts[i];
var nextPt = pts[i + 1];
//首先判断point是否在curPt和nextPt之间，即：此判断该点是否在该线段的外包矩形内
if (
point.lng >= Math.min(curPt.lng, nextPt.lng) &&
point.lng <= Math.max(curPt.lng, nextPt.lng) &&
point.lat >= Math.min(curPt.lat, nextPt.lat) &&
point.lat <= Math.max(curPt.lat, nextPt.lat)
) {
//判断点是否在直线上公式
var precision =
(curPt.lng - point.lng) * (nextPt.lat - point.lat) -
(nextPt.lng - point.lng) * (curPt.lat - point.lat);
if (precision < 2e-9 && precision > -2e-9) {
//实质判断是否接近0
return true;
}
}
}
return false;
};
/**
* 判断点是否多边形内
* @param {Point} point 点对象
* @param {Polyline} polygon 多边形对象
* @returns {Boolean} 点在多边形内返回true,否则返回false
*/
GeoUtils.isPointInPolygon = function (point, polygon) {
//检查类型
if (
!(point.toString() === "Point" || point.toString() === "LatLng") ||
!(polygon instanceof BMapGL.Polygon)
) {
return false;
}
//首先判断点是否在多边形的外包矩形内，如果在，则进一步判断，否则返回false
var polygonBounds = polygon.getBounds();
if (!this.isPointInRect(point, polygonBounds)) {
return false;
}
var pts = polygon.getPath(); //获取多边形点
//下述代码来源：http://paulbourke.net/geometry/insidepoly/，进行了部分修改
//基本思想是利用射线法，计算射线与多边形各边的交点，如果是偶数，则点在多边形外，否则
//在多边形内。还会考虑一些特殊情况，如点在多边形顶点上，点在多边形边上等特殊情况。
var N = pts.length;
var boundOrVertex = true; //如果点位于多边形的顶点或边上，也算做点在多边形内，直接返回true
var intersectCount = 0; //cross points count of x
var precision = 2e-10; //浮点类型计算时候与0比较时候的容差
var p1, p2; //neighbour bound vertices
var p = point; //测试点
p1 = pts[0]; //left vertex
for (var i = 1; i <= N; ++i) {
//check all rays
if (p.equals(p1)) {
return boundOrVertex; //p is an vertex
}
p2 = pts[i % N]; //right vertex
if (
p.lat < Math.min(p1.lat, p2.lat) ||
p.lat > Math.max(p1.lat, p2.lat)
) {
//ray is outside of our interests
p1 = p2;
continue; //next ray left point
}
if (
p.lat > Math.min(p1.lat, p2.lat) &&
p.lat < Math.max(p1.lat, p2.lat)
) {
//ray is crossing over by the algorithm (common part of)
if (p.lng <= Math.max(p1.lng, p2.lng)) {
//x is before of ray
if (p1.lat == p2.lat && p.lng >= Math.min(p1.lng, p2.lng)) {
//overlies on a horizontal ray
return boundOrVertex;
}
if (p1.lng == p2.lng) {
//ray is vertical
if (p1.lng == p.lng) {
//overlies on a vertical ray
return boundOrVertex;
} else {
//before ray
++intersectCount;
}
} else {
//cross point on the left side
var xinters =
((p.lat - p1.lat) * (p2.lng - p1.lng)) /
(p2.lat - p1.lat) +
p1.lng; //cross point of lng
if (Math.abs(p.lng - xinters) < precision) {
//overlies on a ray
return boundOrVertex;
}
if (p.lng < xinters) {
//before ray
++intersectCount;
}
}
}
} else {
//special case when ray is crossing through the vertex
if (p.lat == p2.lat && p.lng <= p2.lng) {
//p crossing over p2
var p3 = pts[(i + 1) % N]; //next vertex
if (
p.lat >= Math.min(p1.lat, p3.lat) &&
p.lat <= Math.max(p1.lat, p3.lat)
) {
//p.lat lies between p1.lat & p3.lat
++intersectCount;
} else {
intersectCount += 2;
}
}
}
p1 = p2; //next ray left point
}
if (intersectCount % 2 == 0) {
//偶数在多边形外
return false;
} else {
//奇数在多边形内
return true;
}
};
/**
* 将度转化为弧度
* @param {degree} Number 度
* @returns {Number} 弧度
*/
GeoUtils.degreeToRad = function (degree) {
return (Math.PI * degree) / 180;
};
/**
* 将弧度转化为度
* @param {radian} Number 弧度
* @returns {Number} 度
*/
GeoUtils.radToDegree = function (rad) {
return (180 * rad) / Math.PI;
};
/**
* 将v值限定在a,b之间，纬度使用
*/
function _getRange(v, a, b) {
if (a != null) {
v = Math.max(v, a);
}
if (b != null) {
v = Math.min(v, b);
}
return v;
}
/**
* 将v值限定在a,b之间，经度使用
*/
function _getLoop(v, a, b) {
while (v > b) {
v -= b - a;
}
while (v < a) {
v += b - a;
}
return v;
}
/**
* 计算两点之间的距离,两点坐标必须为经纬度
* @param {point1} Point 点对象
* @param {point2} Point 点对象
* @returns {Number} 两点之间距离，单位为米
*/
GeoUtils.getDistance = function (point1, point2) {
//判断类型
if (
!(
point1.toString() === "Point" ||
point1.toString() === "LatLng" ||
point2.toString() === "Point" ||
point2.toString() === "LatLng"
)
) {
return 0;
}
point1.lng = _getLoop(point1.lng, -180, 180);
point1.lat = _getRange(point1.lat, -74, 74);
point2.lng = _getLoop(point2.lng, -180, 180);
point2.lat = _getRange(point2.lat, -74, 74);
var x1, x2, y1, y2;
x1 = GeoUtils.degreeToRad(point1.lng);
y1 = GeoUtils.degreeToRad(point1.lat);
x2 = GeoUtils.degreeToRad(point2.lng);
y2 = GeoUtils.degreeToRad(point2.lat);
return (
EARTHRADIUS *
Math.acos(
Math.sin(y1) * Math.sin(y2) +
Math.cos(y1) * Math.cos(y2) * Math.cos(x2 - x1)
)
);
};
/**
* 计算折线或者点数组的长度
* @param {Polyline|Array<Point>} polyline 折线对象或者点数组
* @returns {Number} 折线或点数组对应的长度
*/
GeoUtils.getPolylineDistance = function (polyline) {
//检查类型
if (polyline instanceof BMapGL.Polyline || polyline instanceof Array) {
//将polyline统一为数组
var pts;
if (polyline instanceof BMapGL.Polyline) {
pts = polyline.getPath();
} else {
pts = polyline;
}
if (pts.length < 2) {
//小于2个点，返回0
return 0;
}
//遍历所有线段将其相加，计算整条线段的长度
var totalDis = 0;
for (var i = 0; i < pts.length - 1; i++) {
var curPt = pts[i];
var nextPt = pts[i + 1];
var dis = GeoUtils.getDistance(curPt, nextPt);
totalDis += dis;
}
return totalDis;
} else {
return 0;
}
};
/**
* 计算多边形面或点数组构建图形的面积,注意：坐标类型只能是经纬度，且不适合计算自相交多边形的面积
* @param {Polygon|Array<Point>} polygon 多边形面对象或者点数组
* @returns {Number} 多边形面或点数组构成图形的面积
*/
GeoUtils.getPolygonArea = function (polygon) {
//检查类型
if (
!(polygon instanceof BMapGL.Polygon) &&
!(polygon instanceof Array)
) {
return 0;
}
var pts;
if (polygon instanceof BMapGL.Polygon) {
pts = polygon.getPath();
} else {
pts = polygon;
}
if (pts[0].equals(pts[pts.length - 1])) {
pts.pop();
}
if (pts.length < 3) {
//小于3个顶点，不能构建面
return 0;
}
var totalArea = 0; //初始化总面积
var LowX = 0.0;
var LowY = 0.0;
var MiddleX = 0.0;
var MiddleY = 0.0;
var HighX = 0.0;
var HighY = 0.0;
var AM = 0.0;
var BM = 0.0;
var CM = 0.0;
var AL = 0.0;
var BL = 0.0;
var CL = 0.0;
var AH = 0.0;
var BH = 0.0;
var CH = 0.0;
var CoefficientL = 0.0;
var CoefficientH = 0.0;
var ALtangent = 0.0;
var BLtangent = 0.0;
var CLtangent = 0.0;
var AHtangent = 0.0;
var BHtangent = 0.0;
var CHtangent = 0.0;
var ANormalLine = 0.0;
var BNormalLine = 0.0;
var CNormalLine = 0.0;
var OrientationValue = 0.0;
var AngleCos = 0.0;
var Sum1 = 0.0;
var Sum2 = 0.0;
var Count2 = 0;
var Count1 = 0;
var Sum = 0.0;
var Radius = EARTHRADIUS; //6378137.0,WGS84椭球半径
var Count = pts.length;
for (var i = 0; i < Count; i++) {
if (i == 0) {
LowX = (pts[Count - 1].lng * Math.PI) / 180;
LowY = (pts[Count - 1].lat * Math.PI) / 180;
MiddleX = (pts[0].lng * Math.PI) / 180;
MiddleY = (pts[0].lat * Math.PI) / 180;
HighX = (pts[1].lng * Math.PI) / 180;
HighY = (pts[1].lat * Math.PI) / 180;
} else if (i == Count - 1) {
LowX = (pts[Count - 2].lng * Math.PI) / 180;
LowY = (pts[Count - 2].lat * Math.PI) / 180;
MiddleX = (pts[Count - 1].lng * Math.PI) / 180;
MiddleY = (pts[Count - 1].lat * Math.PI) / 180;
HighX = (pts[0].lng * Math.PI) / 180;
HighY = (pts[0].lat * Math.PI) / 180;
} else {
LowX = (pts[i - 1].lng * Math.PI) / 180;
LowY = (pts[i - 1].lat * Math.PI) / 180;
MiddleX = (pts[i].lng * Math.PI) / 180;
MiddleY = (pts[i].lat * Math.PI) / 180;
HighX = (pts[i + 1].lng * Math.PI) / 180;
HighY = (pts[i + 1].lat * Math.PI) / 180;
}
AM = Math.cos(MiddleY) * Math.cos(MiddleX);
BM = Math.cos(MiddleY) * Math.sin(MiddleX);
CM = Math.sin(MiddleY);
AL = Math.cos(LowY) * Math.cos(LowX);
BL = Math.cos(LowY) * Math.sin(LowX);
CL = Math.sin(LowY);
AH = Math.cos(HighY) * Math.cos(HighX);
BH = Math.cos(HighY) * Math.sin(HighX);
CH = Math.sin(HighY);
CoefficientL =
(AM * AM + BM * BM + CM * CM) / (AM * AL + BM * BL + CM * CL);
CoefficientH =
(AM * AM + BM * BM + CM * CM) / (AM * AH + BM * BH + CM * CH);
ALtangent = CoefficientL * AL - AM;
BLtangent = CoefficientL * BL - BM;
CLtangent = CoefficientL * CL - CM;
AHtangent = CoefficientH * AH - AM;
BHtangent = CoefficientH * BH - BM;
CHtangent = CoefficientH * CH - CM;
AngleCos =
(AHtangent * ALtangent +
BHtangent * BLtangent +
CHtangent * CLtangent) /
(Math.sqrt(
AHtangent * AHtangent +
BHtangent * BHtangent +
CHtangent * CHtangent
) *
Math.sqrt(
ALtangent * ALtangent +
BLtangent * BLtangent +
CLtangent * CLtangent
));
if (AngleCos < -1.0) AngleCos = -1.0;
if (AngleCos > 1.0) AngleCos = 1.0;
AngleCos = Math.acos(AngleCos);
ANormalLine = BHtangent * CLtangent - CHtangent * BLtangent;
BNormalLine = 0 - (AHtangent * CLtangent - CHtangent * ALtangent);
CNormalLine = AHtangent * BLtangent - BHtangent * ALtangent;
if (AM != 0) OrientationValue = ANormalLine / AM;
else if (BM != 0) OrientationValue = BNormalLine / BM;
else OrientationValue = CNormalLine / CM;
if (OrientationValue > 0) {
Sum1 += AngleCos;
Count1++;
} else {
Sum2 += AngleCos;
Count2++;
}
}
var tempSum1, tempSum2;
tempSum1 = Sum1 + (2 * Math.PI * Count2 - Sum2);
tempSum2 = 2 * Math.PI * Count1 - Sum1 + Sum2;
if (Sum1 > Sum2) {
if (tempSum1 - (Count - 2) * Math.PI < 1) Sum = tempSum1;
else Sum = tempSum2;
} else {
if (tempSum2 - (Count - 2) * Math.PI < 1) Sum = tempSum2;
else Sum = tempSum1;
}
totalArea = (Sum - (Count - 2) * Math.PI) * Radius * Radius;
return totalArea; //返回总面积
};
/**
* 判断折线与多边形是否相交
* 参考：https://www.cnblogs.com/tuyang1129/p/9390376.html
* @param {Polyline|Array<Point>} lines 折线
* @param {Polygon|Array<Point>} polygon 多边形
* @returns {Boolean} 折线和多边形是否相交
*/
GeoUtils.isPolylineIntersectArea = function (lines, polygon) {
var segmentIntersect = function (a, b, c, d) {
var x1 = a.lng, y1 = a.lat;
var x2 = b.lng, y2 = b.lat;
var x3 = c.lng, y3 = c.lat;
var x4 = d.lng, y4 = d.lat;
if (!(Math.min(x1, x2) <= Math.max(x3, x4) && Math.min(y3, y4) <= Math.max(y1, y2) && Math.min(x3, x4) <= Math.max(x1, x2) && Math.min(y1, y2) <= Math.max(y3, y4)))
return false;
var u, v, w, z
u = (x3 - x1) * (y2 - y1) - (x2 - x1) * (y3 - y1);
v = (x4 - x1) * (y2 - y1) - (x2 - x1) * (y4 - y1);
w = (x1 - x3) * (y4 - y3) - (x4 - x3) * (y1 - y3);
z = (x2 - x3) * (y4 - y3) - (x4 - x3) * (y2 - y3);
return (u * v <= 2e-10 && w * z <= 2e-10);
}
if (!(lines instanceof BMapGL.Polyline && polygon instanceof BMapGL.Polygon)) {
console.error('参数出错,传入值非折线和多边形')
return false;
}
lines = lines.getPath().map(function (point) {
return {'lng': point.lng, 'lat': point.lat}
});
polygon = polygon.getPath().map(function (point) {
return {'lng': point.lng, lat: point.lat}
});
// 包含点的判断
if (lines.length < 1 || polygon.length <= 2) {
console.error('参数出错,传入值非折线和多边形')
return false;
}
var maybeLine = [], ploygonLine = [];
// 遍历所有点 在内部直接返回true
for (var j = 0; j < lines.length; j++) {
if (GeoUtils.isPointInPolygon(lines[j], polygon)) {
return true;
}
}
for (var n = 1; n < lines.length; n++) {
maybeLine.push([lines[n - 1], lines[n]]);
}
for (var k = 1; k < polygon.length; k++) {
ploygonLine.push([polygon[k - 1], polygon[k]]);
}
ploygonLine.push([polygon[polygon.length - 1], polygon[0]]);
// 折线与多边形边若相交则返回true
for (var l = 0; l < maybeLine.length; l++) {
for (var m = 0; m < ploygonLine.length; m++) {
if (segmentIntersect(maybeLine[l][0], maybeLine[l][1], ploygonLine[m][0], ploygonLine[m][1])) return true;
}
}
return false;
}
})(); //闭包结束
示例测试： 其中BMapGL使用的依赖需要提供下百度API的ak秘钥 获取地址： https://lbsyun.baidu.com/apiconsole/key?application=key#/home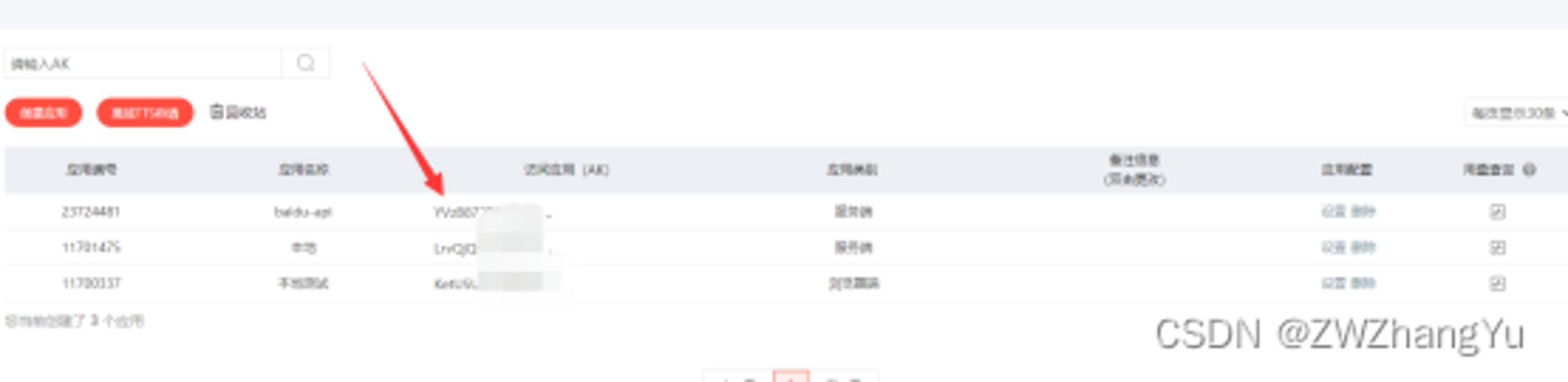 
<script type="text/javascript"
src="https://api.map.baidu.com/api?v=1.0&&type=webgl&ak=XXX"></script>
<script type="text/javascript" src="./GeoUtils.js"></script>
<script>
// 测试点是否在矩形内
function ptInRect() {
var pt = new BMapGL.Point(116.404, 39.915); // 测试点
var pt1 = new BMapGL.Point(116.400, 39.910); // 西南脚点
var pt2 = new BMapGL.Point(116.410, 39.920); // 东北脚点
var bds = new BMapGL.Bounds(pt1, pt2);
var result = BMapGLLib.GeoUtils.isPointInRect(pt, bds);
if (result == true) {
alert('点在矩形内');
} else {
alert('点在矩形外');
}
}
// 测试点是否在圆内
function ptInCircle() {
var pt = new BMapGL.Point(116.404, 39.915); // 测试点
var c = new BMapGL.Point(116.404, 39.915); // 圆心
var circle = new BMapGL.Circle(c, 500); // 测试圆
var result = BMapGLLib.GeoUtils.isPointInCircle(pt, circle);
if (result == true) {
alert('点在圆形内');
} else {
alert('点在圆形外');
}
}
</script>
高德地图
文档地址： https://lbs.amap.com/demo/javascript-api/example/calcutation/calculate-distance-between-two-markers https://lbs.amap.com/api/javascript-api/reference/math
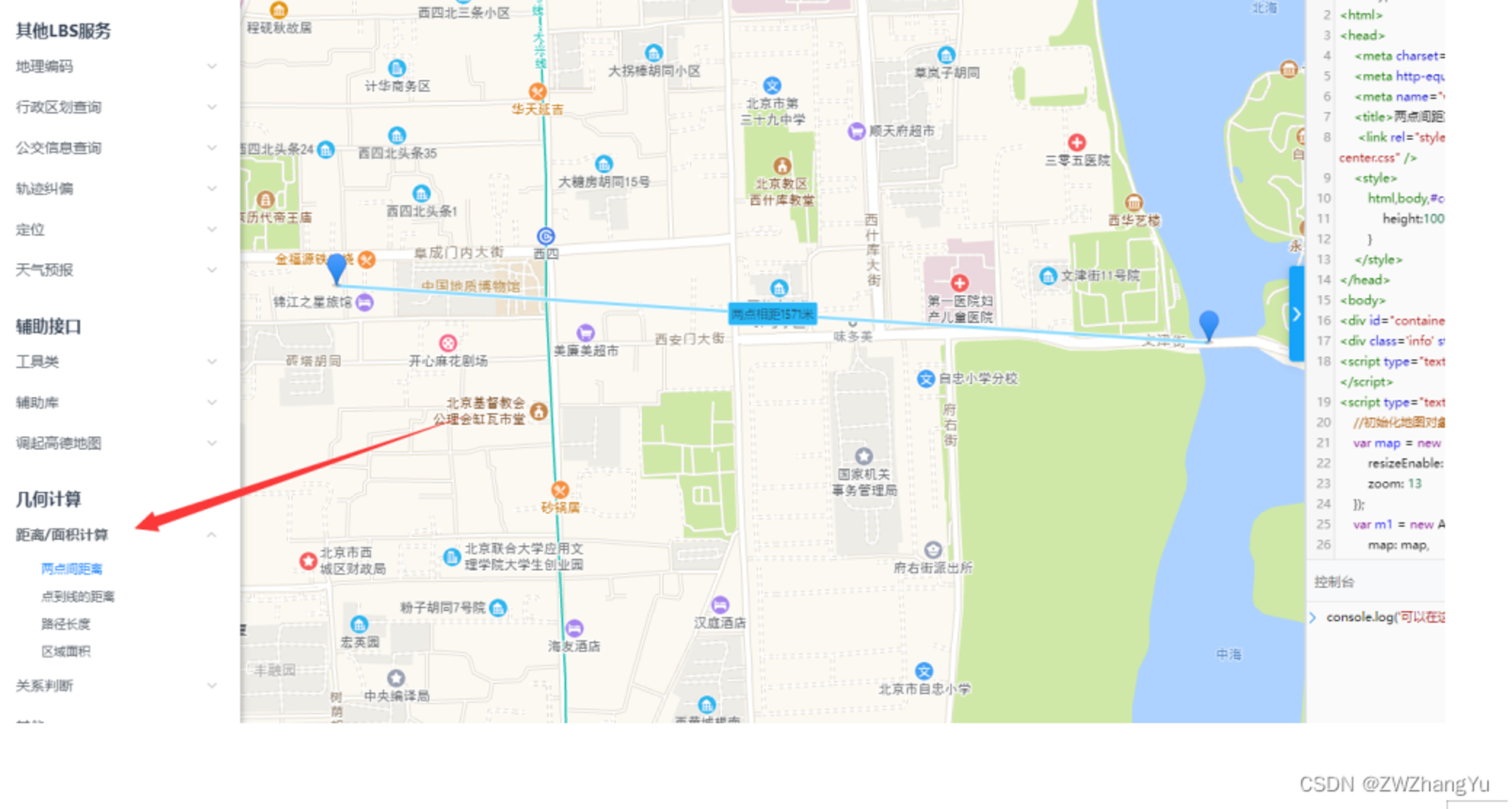
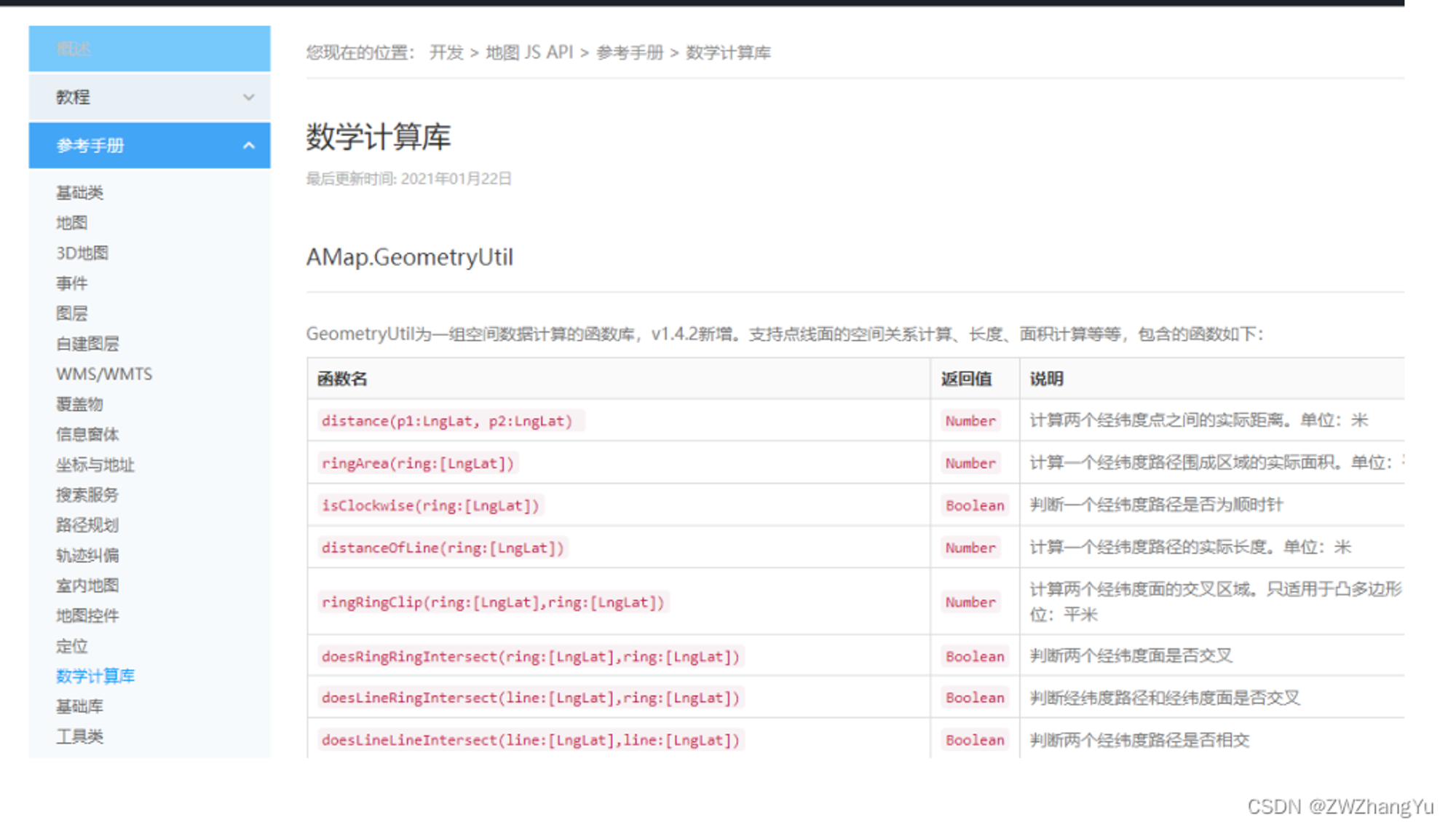
更多内容可见我的另一篇文章 关于地图GIS的一次实践整理（下） Redis的GIS实践
边栏推荐
- 定了！8月起，网易将为本号粉丝提供数据分析培训，费用全免！
- Introduction to resubmit Progressive Anti-Duplicate Submission Framework
- 最近公共祖先（LCA）学习笔记 | P3379 【模板】最近公共祖先（LCA）题解
- D experimental new anomaly
- 微信小程序实现lot开发09 接入微信登录
- pytest-常用运行参数
- MySQL的多表查询（1）
- Find My技术|智能防丢还得看苹果Find My技术
- Teach you to locate online MySQL slow query problem hand by hand, package teaching package meeting
- d实验新异常
猜你喜欢
【斯坦福计网CS144项目】Lab5: NetworkInterface
程序员的七夕浪漫时刻
js基础知识整理之 —— Math
漫画：怎么证明sleep不释放锁，而wait释放锁？
VMware workstation program starts slowly
用了这么多年的LinkedList，作者说自己从来不用它？为什么？
智能电视竞争白热化，利用小程序共建生态突围
同一份数据，Redis为什么要存两次？
Visual Studio中vim模拟器
Technology Sharing | How to do assertion verification for xml format in interface automation testing?
随机推荐
心电记录电路设计(框图/波形以及信号放大器的选择)
js基础知识整理之 —— 获取元素和命名规范
matplotlib中的3D绘图警告解决：MatplotlibDeprecationWarning: Axes3D(fig) adding itself to the figure
Day117. Shangyitong: Generate registered order module
剑指 Offer 21. 调整数组顺序使奇数位于偶数前面
KubeSphere监控失效为NAN的问题
Nlog自定义时间
函数：计算组合数
定了！8月起，网易将为本号粉丝提供数据分析培训，费用全免！
Day117.尚医通：生成挂号订单模块
CAS:1445723-73-8,DSPE-PEG-NHS,磷脂-聚乙二醇-活性酯两亲性脂质PEG共轭物
程序员的七夕浪漫时刻
【Autosar RTM】
1 - vector R language self-study
优秀论文以及思路分析01
十三、数据回显
程序员如何优雅地解决线上问题？
Moco of Mock tools use tutorial
【QT】自定义工程封装成DLL并如何调用（带ui界面的）
十年架构五年生活-05第一次出差