当前位置:网站首页>【GIoU loss】GIoU loss损失函数理解
【GIoU loss】GIoU loss损失函数理解
2022-08-03 05:27:00 【寻找永不遗憾】
1 引言
目标检测任务的损失函数由Classificition Loss和Bounding Box Regeression Loss两部分构成。
Bounding Box Regression Loss Function的演进路线是:
Smooth L1 Loss --> IoU Loss --> GIoU Loss --> DIoU Loss --> CIoU Loss
之前写到了 Smooth L1 Loss 和 IoU Loss。
本文介绍GIoU Loss。
2 问题分析
IoU Loss 存在的问题:
- 当预测框和目标框不相交时 ,IoU(A,B)=0时,不能反映A,B距离的远近,此时损失函数不可导,IoU Loss 无法优化两个框不相交的情况。
- 假设预测框和目标框的大小都确定,只要两个框的相交值是确定的,那么IoU值就相同,IoU值不能反映两个框是如何相交的。
3 GIoU Loss计算过程
GIoU Loss计算过程如下: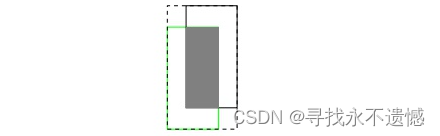
以上图为例,绿色框表示预测框 B p = ( x 1 p , y 1 p , x 2 p , y 2 p ) B^p=(x_1^p,y_1^p,x_2^p,y_2^p) Bp=(x1p,y1p,x2p,y2p),黑色框表示边界框 B g = ( x 1 g , y 1 g , x 2 g , y 2 g ) B^g=(x_1^g,y_1^g,x_2^g,y_2^g) Bg=(x1g,y1g,x2g,y2g),首先计算IoU:
I o U = I U IoU = \frac{I}{U} IoU=UI
其中, I I I 表示:上图中的灰色阴影部分, U U U 表示:两个矩形面积之和 ( A p + A g ) (A^p +A^g) (Ap+Ag)减去两个矩形相交的面积 I I I,因此IoU也可以表示为: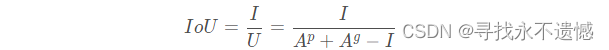
GIoU在IoU基础上,考虑了两个矩形最小闭包(the smallest enclosing convex object,两个矩形的最小外接矩形)的大小,GIoU的计算表达式为: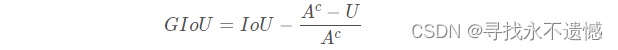
其中, − 1 ≤ G I o U < 1 -1≤GIoU<1 −1≤GIoU<1, A c A^c Ac是两个矩形的最小外接矩形的面积,也就是上图中虚线框的面积。
G I o U L o s s = 1 − G I o U GIoU Loss = 1-GIoU GIoULoss=1−GIoU
此时 0 < G I o U L o s s ≤ 2 0<GIoU Loss≤2 0<GIoULoss≤2。
4 IoU和GIoU对比分析
算法计算过程对比:

可见计算GIoU损失的方式其实就是计算GIoU,只不过最终结果返回的是1-GIoU。
这是因为1-GIoU的取值范围在[0,2]上,且有一定的“距离”性质,即两个框重叠区域越大,损失越小,反之越大。图看GIoU到底解决了IoU的什么问题
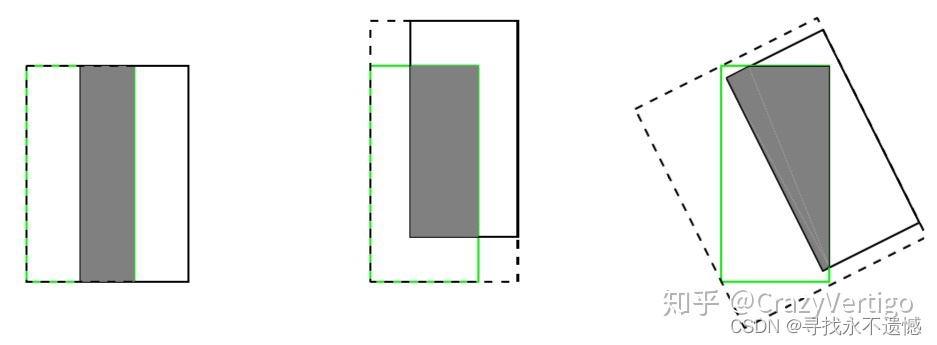
如上图所示,三种不同相对位置的框拥有相同的IoU=0.33值,但是拥有不同的GIoU=0.33,0.24,-0.1。当框的对齐方向更好一些时GIoU的值会更高一些。
5 代码实现IoU与GIoU的对比可视化
很简单,直接看代码注释即可。
import numpy as np
import cv2
def CountIOU(RecA, RecB):
xA = max(RecA[0], RecB[0])
yA = max(RecA[1], RecB[1])
xB = min(RecA[2], RecB[2])
yB = min(RecA[3], RecB[3])
# 计算交集部分面积
interArea = max(0, xB - xA + 1) * max(0, yB - yA + 1)
# 计算预测值和真实值的面积
RecA_Area = (RecA[2] - RecA[0] + 1) * (RecA[3] - RecA[1] + 1)
RecB_Area = (RecB[2] - RecB[0] + 1) * (RecB[3] - RecB[1] + 1)
# 计算IOU
iou = interArea / float(RecA_Area + RecB_Area - interArea)
return iou
def Giou(rec1,rec2):
# 分别是矩形左上、右下的坐标
x1,y1,x2,y2 = rec1
x3,y3,x4,y4 = rec2
iou = CountIOU(rec1,rec2)
area_C = (max(x1,x2,x3,x4)-min(x1,x2,x3,x4))*(max(y1,y2,y3,y4)-min(y1,y2,y3,y4))
area_1 = (x2-x1)*(y1-y2)
area_2 = (x4-x3)*(y3-y4)
sum_area = area_1 + area_2
w1 = x2 - x1 #第一个矩形的宽
w2 = x4 - x3 #第二个矩形的宽
h1 = y1 - y2
h2 = y3 - y4
W = min(x1,x2,x3,x4)+w1+w2-max(x1,x2,x3,x4) # 交叉部分的宽
H = min(y1,y2,y3,y4)+h1+h2-max(y1,y2,y3,y4) # 交叉部分的高
# 交叉的面积
Area = W * H
# 两矩形并集的面积
add_area = sum_area - Area
# 闭包区域中不属于两个框的区域占闭包区域的比重
end_area = (area_C - add_area)/area_C
giou = iou - end_area
return giou
img = np.zeros((512,512,3), np.uint8)
img.fill(255)
# 分别是矩形左上、右下的坐标
RecA = [30,30,300,300]
RecB = [60,60,350,340]
cv2.rectangle(img, (RecA[0],RecA[1]), (RecA[2],RecA[3]), (0, 255, 0), 5)
cv2.rectangle(img, (RecB[0],RecB[1]), (RecB[2],RecB[3]), (255, 0, 0), 5)
IOU = CountIOU(RecA,RecB)
GIoU = Giou(RecA,RecB)
font = cv2.FONT_HERSHEY_SIMPLEX
cv2.putText(img,"IOU = %.2f"%IOU,(130, 190),font,0.8,(0,0,0),2)
cv2.putText(img,"GIOU = %.2f"%GIoU,(130, 220),font,0.8,(0,0,0),2)
cv2.imshow("image",img)
cv2.waitKey()
cv2.destroyAllWindows()

6 感谢链接
https://zhuanlan.zhihu.com/p/104236411
https://blog.csdn.net/A_A666/article/details/111504851
https://zhuanlan.zhihu.com/p/94799295
边栏推荐
猜你喜欢
随机推荐
数组与字符串13-两数之和等于目标数
2021-06-15
Migration of BOA Server
g++ parameter description
Monitoring Oracle11gR2 in Zabbix6.0 of OracleLinux8.6
cobalt strike 的基础使用
守望先锋英雄角色模型分享,obj文件+材质贴图,3dmax游戏建模
2021-06-15
二分查找5 - 第一个错误的版本
【面筋1】一些没什么标准答案的问题
数组与字符串11-反转字符串
servlet learning (7) ServletContext
用DirectX12绘制一个几何体的程序详述
SQLMAP介绍及使用
数据库OracleRAC节点宕机处理流程
ESXI主机给虚拟机添加USB加密狗设备
3D建模为什么会变得无处不在
MySQL的主从复制
嘿!selenium自动下载driver版本,得知道一下
使用ZBrush制作恶魔模型