当前位置:网站首页>每日一题:连续子数组的最大和(动态规划)
每日一题:连续子数组的最大和(动态规划)
2022-08-01 10:51:00 【利刃Cc】
知识点动态规划
描述
输入一个长度为n的整型数组array,数组中的一个或连续多个整数组成一个子数组,子数组最小长度为1。求所有子数组的和的最大值。
数据范围:
1 <= n <= 2*10^5
-100 <= a[i] <= 100
要求:时间复杂度为 O(n)O(n),空间复杂度为 O(n)O(n)
进阶:时间复杂度为 O(n)O(n),空间复杂度为 O(1)O(1)
示例1
输入:[1,-2,3,10,-4,7,2,-5]
返回值18
说明:经分析可知,输入数组的子数组[3,10,-4,7,2]可以求得最大和为18
示例2
输入:
输入:[2]
返回值:2
示例3
输入:
输入:[-10]
返回值:-10
解题思路
方法1: 连续的子数组,即数组中从i下标到j下标(0<=i<=j<数组长度)的数据,想要获得所有的子数组和,可以通过暴力法,两次循环获得,但时间复杂度为O(n^2),效率不高。
方法2: 动态规划,设动态规划列表 dp,dp[i] 代表以元素 array[i] 为结尾的连续子数组最大和。
状态转移方程: dp[i] = max(dp[i-1] + array[i], array[i]);
具体思路如下:
1、遍历数组,比较 dp[i-1] + array[i] 和 array[i]的大小;
2、为了保证子数组的和最大,每次比较 sum 都取两者的最大值;
3、用max变量记录计算过程中产生的最大的连续和dp[i];
方法3: 我们可以简化动态规划,使用一个变量sum来表示当前连续的子数组和,以及一个变量max来表示中间出现的最大的和。
代码实现
方法1:暴力法,时间复杂度O(n^2),空间复杂度O(1)
class Solution {
public:
int FindGreatestSumOfSubArray(vector<int> array) {
int Max = array[0];
int sum = 0;
for(int i = 0; i < array.size(); ++i)
{
// 每开启新的循环,需要把sum归零
sum = 0;
for(int j = i; j < array.size(); ++j)
{
// 这里是求从i到j的数值和
sum += array[j];
// 每次比较,保存出现的最大值
Max = max(Max, sum);
}
}
return Max;
}
};
方法2:动态规划,时间复杂度O(n),空间复杂度O(n)
class Solution {
public:
int FindGreatestSumOfSubArray(vector<int> array) {
int* dp = new int[array.size()];
int Max = array[0];
dp[0] = array[0];
for(int i = 1; i < array.size(); ++i)
{
// 动态规划,状态转移方程,确定dp[i]的最大值
dp[i] = max(dp[i - 1] + array[i], array[i]);
// 每次比较,保存出现的最大值
Max = max(Max, dp[i]);
}
return Max;
}
};
方法3:优化动态规划,时间复杂度O(n),空间复杂度O(1)
class Solution {
public:
int FindGreatestSumOfSubArray(vector<int> array) {
if(array.empty())
return 0;
int Max = array[0];
int sum = array[0];
for(int i = 1; i < array.size(); ++i)
{
// 优化动态规划,确定sum的最大值
sum = max(sum + array[i], array[i]);
// 每次比较,保存出现的最大值
Max = max(Max, sum);
}
return Max;
}
};
另一种写法:不用max的写法,就是用 if语句代替
/* 算法时间复杂度 O(n) 用cur记录累计值,maxSum记录和最大 基于思想:对于一个数A,若是A的左边累计数非负,那么加上A能使得值不小于A,认为累计值对 整体和是有贡献的。如果前几项累计值负数,则认为有害于总和,cur记录当前值。 此时 若和大于maxSum 则用maxSum记录下来 */
class Solution {
public:
int FindGreatestSumOfSubArray(vector<int> array) {
if(array.empty())
return 0;
int maxSum = array[0];
int cur = array[0];
for(int i = 1; i < array.size(); ++i)
{
if(cur >= 0)
cur += array[i];
else
cur = array[i];
if(cur > maxSum)
maxSum = cur;
}
return maxSum;
}
};
边栏推荐
- 编码解码(btoa、encodeURIComponent、encodeURI、escape)
- 【cartographer ros】十: 延时和误差分析
- MySQL 必现之死锁
- 小程序毕设作品之微信美食菜谱小程序毕业设计成品(3)后台功能
- mysql login in cmd and basic operations of database and table
- Custom Types - Enums, Unions
- 深度学习 | MATLAB实现GRU门控循环单元gruLayer参数设定
- 开天aPaaS之移动手机号码空号检测【开天aPaaS大作战】
- Dapr 与 NestJs ,实战编写一个 Pub & Sub 装饰器
- 从零开始Blazor Server(4)--登录系统
猜你喜欢

【钛晨报】国家统计局:7月制造业PMI为49%;玖富旗下理财产品涉嫌欺诈,涉及390亿元;国内航线机票燃油附加费8月5日0时起下调

Mini Program Graduation Works WeChat Food Recipes Mini Program Graduation Design Finished Products (4) Opening Report

LeakCanary如何监听Service、Root View销毁时机?

小程序毕设作品之微信美食菜谱小程序毕业设计成品(1)开发概要

redis6 跟着b站尚硅谷学习
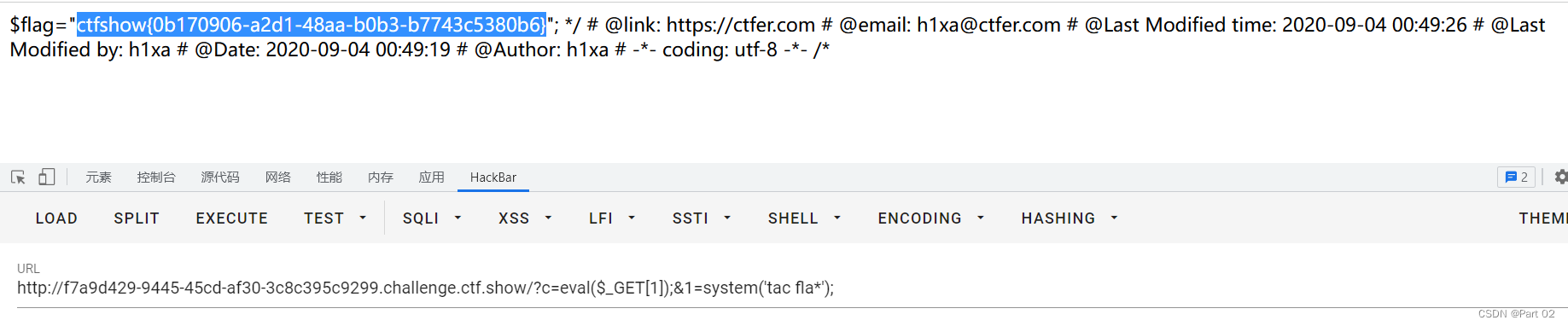
CTFshow,命令执行:web31

Flutter Widget 如何启用和屏蔽点击事件
回归预测 | MATLAB实现TPA-LSTM(时间注意力注意力机制长短期记忆神经网络)多输入单输出

Mysql索引相关的知识复盘一

AI篮球裁判火了,走步算得特别准,就问哈登慌不慌
随机推荐
Guangyu Mingdao was selected into the list of pilot demonstration projects for the development of digital economy industry in Chongqing in 2022
上周热点回顾(7.25-7.31)
ClickHouse多种安装方式
STM32 Personal Notes - Embedded C Language Optimization
Promise learning (1) What is Promise?how to use?How to solve callback hell?
深度学习 | MATLAB实现一维卷积神经网络convolution1dLayer参数设定
PDMan-国产免费通用数据库建模工具(极简,漂亮)
MySQL常用语句总结
redis6 跟着b站尚硅谷学习
【钛晨报】国家统计局:7月制造业PMI为49%;玖富旗下理财产品涉嫌欺诈,涉及390亿元;国内航线机票燃油附加费8月5日0时起下调
Dataset之mpg:mpg数据集的简介、下载、使用方法之详细攻略
将本地项目推送到远程仓库
编码解码(btoa、encodeURIComponent、encodeURI、escape)
PowerPC技术与市场杂谈
gc的意义和触发条件
MySQL 必现之死锁
C#/VB.NET 将PPT或PPTX转换为图像
深度学习 | MATLAB实现GRU门控循环单元gruLayer参数设定
小程序毕设作品之微信美食菜谱小程序毕业设计成品(3)后台功能
Introduction and application of pointers