当前位置:网站首页>Johnson–Lindenstrauss Lemma
Johnson–Lindenstrauss Lemma
2022-07-04 02:14:00 【FakeOccupational】
Johnson–Lindenstrauss lemma

lemma : Given ϵ > 0 \epsilon>0 ϵ>0, Random vector module length varies with n Converge exponentially to 1.
along with machine towards The amount x ∈ R n in Of Every time individual sit mark Mining sample since N ( 0 , 1 n ) P ( ∣ ∥ x ∥ 2 − 1 ∣ ≥ ε ) ≤ 2 exp ( − ε 2 n 8 ) Random vector x\in R^n Each coordinate in is sampled from N(0,\frac{1}{n})\\ P(|\Vert x\Vert^2 - 1| \geq \varepsilon) \leq 2\exp\left(-\frac{\varepsilon^2 n}{8}\right) along with machine towards The amount x∈Rn in Of Every time individual sit mark Mining sample since N(0,n1)P(∣∥x∥2−1∣≥ε)≤2exp(−8ε2n)
lemma : Also sample two random vectors , Approximately orthogonal .
P ( ∣ * x 1 , x 2 * ∣ ≥ ε ) ≤ 4 exp ( − ε 2 n 8 ) P(|\langle x_1, x_2\rangle| \geq \varepsilon) \leq 4\exp\left(-\frac{\varepsilon^2 n}{8}\right) P(∣*x1,x2*∣≥ε)≤4exp(−8ε2n)
Johnson–Lindenstrauss Lemma
Given ϵ > 0 \epsilon>0 ϵ>0, x i ∈ R m ( i = 1 , … , N ) , Such as On Mining sample Out One individual along with machine Moment front A ∈ R n × m , n > 24 log N ε 2 x_i \in R^m(i=1,…,N), A random matrix is sampled as above A\in \R^{n×m},n > \frac{24\log N}{\varepsilon^2} xi∈Rm(i=1,…,N), Such as On Mining sample Out One individual along with machine Moment front A∈Rn×m,n>ε224logN
( 1 − ε ) ∥ v i − v j ∥ 2 ≤ ∥ A v i − A v j ∥ 2 ≤ ( 1 + ε ) ∥ v i − v j ∥ 2 (1-\varepsilon)\Vert v_i - v_j\Vert^2 \leq \Vert Av_i - A v_j\Vert^2 \leq (1+\varepsilon)\Vert v_i - v_j\Vert^2 (1−ε)∥vi−vj∥2≤∥Avi−Avj∥2≤(1+ε)∥vi−vj∥2
application
Cosine theorem
Calculate the similarity of two sentences , You can use it first TF-IDF Algorithm to generate word frequency vector , Then calculate the cosine angle , The smaller, the more similar .
hash function
hash function (MD5 etc. ) Turn the article into a fixed length string , such as 32 position . In the front-end encryption, I have implemented the right “123456” The encryption .
simhash
The traditional hash function cannot compare the similarity between the two articles .simhash technology , It is Google Algorithm invented to solve large-scale web page de duplication . Use 0,1 Represents the final calculation result , XOR operation for comparison .
Johnson–Lindenstrauss lemma + discretization : In European Space N A little bit , After the same random projection mapping , They will still maintain their original relative positions . Then discretize the result of random projection ( Less than 90° by 1, Greater than 90° by 01 Similar as 1, Otherwise 0), Convenient for calculation and storage .
On the basis of the above ,simhash Word segmentation of the article , For every word hash, Yes hash Result weighting , Merge word vectors ( Add in sequence ), The final result is obtained by dimension reduction and other processing . There are pairs. simhash Explanation of algorithm , It seems that the operation of calculation is different .
2: or − 1 , send use − 1 Just can No take the Yes towards The amount Set in stay One individual like limit . \tiny or -1, Use -1 It is not necessary to concentrate all vectors in one quadrant . or −1, send use −1 Just can No take the Yes towards The amount Set in stay One individual like limit .
Reference resources
Reference resources
Reference resources
High dimensional random
To what extent has the theory of machine learning progressed ?
Du, S. S., Kakade, S. M., Wang, R., & Yang, L. F. (2019). Is a Good Representation Sufficient for Sample Efficient Reinforcement Learning?
Database-friendly random projections:
Johnson-Lindenstrauss with binary coins
attention Application in
DGBR Algorithm
IJCAI’21 Secure Deep Graph Generation with Link Differential Privacy
Horse Er can Husband No etc. type : P ( x ≥ a ) ≤ E [ x ] a cut Than snow Husband No etc. type : P ( ( x − E [ x ] ) 2 ≥ a 2 ) ≤ E [ ( x − E [ x ] ) 2 ] a 2 = V a r [ x ] a 2 Markov inequality :P(x\geq a)\leq \frac{\mathbb{E}[x]}{a}\\ Chebyshev inequality :P((x - \mathbb{E}[x])^2\geq a^2) \leq \frac{\mathbb{E}[(x - \mathbb{E}[x])^2]}{a^2}=\frac{\mathbb{V}ar[x]}{a^2} Horse Er can Husband No etc. type :P(x≥a)≤aE[x] cut Than snow Husband No etc. type :P((x−E[x])2≥a2)≤a2E[(x−E[x])2]=a2Var[x]
Bernstein inequality
边栏推荐
- C learning notes: C foundation - Language & characteristics interpretation
- The reasons why QT fails to connect to the database and common solutions
- FRP intranet penetration
- G3 boiler water treatment registration examination and G3 boiler water treatment theory examination in 2022
- From the 18th line to the first line, the new story of the network security industry
- Ai aide à la recherche de plagiat dans le design artistique! L'équipe du professeur Liu Fang a été embauchée par ACM mm, une conférence multimédia de haut niveau.
- Hamburg University of Technology (tuhh) | intelligent problem solving as integrated hierarchical reinforcement learning
- After listening to the system clear message notification, Jerry informed the device side to delete the message [article]
- STM32 key content
- Neo4j learning notes
猜你喜欢

在尋求人類智能AI的過程中,Meta將賭注押向了自監督學習
How to subcontract uniapp and applet, detailed steps (illustration) # yyds dry goods inventory #

From the 18th line to the first line, the new story of the network security industry

Libcblas appears when installing opencv import CV2 so. 3:cannot open shared object file:NO such file or directory
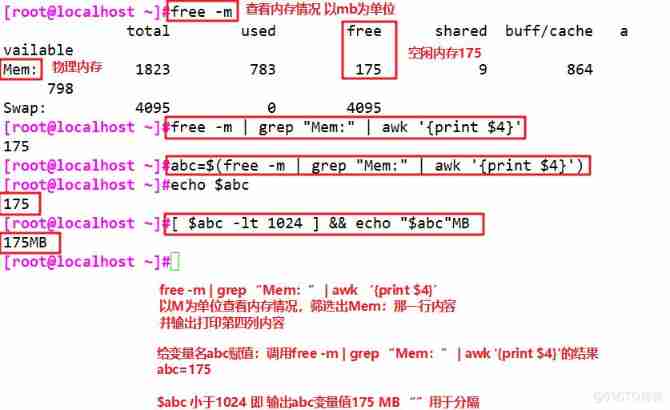
Conditional statements of shell programming

Small program graduation design is based on wechat order takeout small program graduation design opening report function reference
Chapter 3.4: starrocks data import - Flink connector and CDC second level data synchronization

MySQL workbench use
![After listening to the system clear message notification, Jerry informed the device side to delete the message [article]](/img/0c/52816b75eb702c7c63966578ab4969.jpg)
After listening to the system clear message notification, Jerry informed the device side to delete the message [article]

Basic editing specifications and variables of shell script
随机推荐
Flex flexible layout, box in the middle of the page
在尋求人類智能AI的過程中,Meta將賭注押向了自監督學習
The boss said: whoever wants to use double to define the amount of goods, just pack up and go
LV1 previous life archives
Yyds dry goods inventory it's not easy to say I love you | use the minimum web API to upload files
15. System limitations and options
MySQL utilise la vue pour signaler les erreurs, Explicit / show ne peut pas être publié; Verrouillage des fichiers privés pour la table sous - jacente
Libcblas appears when installing opencv import CV2 so. 3:cannot open shared object file:NO such file or directory
Global and Chinese market of small batteries 2022-2028: Research Report on technology, participants, trends, market size and share
Why is the operation unsuccessful (unresolved) uncaught syntaxerror: invalid or unexpected token (resolved)
Idea if a class cannot be found, it will be red
Portapack application development tutorial (XVII) nRF24L01 launch C
Small program graduation project based on wechat e-book small program graduation project opening report function reference
[Yugong series] February 2022 attack and defense world advanced question misc-83 (QR easy)
A. Min Max Swap
MySQL advanced (Advanced) SQL statement (I)
C # learning notes: structure of CS documents
String: LV1 eat hot pot
Take you to master the formatter of visual studio code
Pyrethroid pesticide intermediates - market status and future development trend