当前位置:网站首页>Do you know Dijkstra of graph theory?
Do you know Dijkstra of graph theory?
2022-08-02 12:59:00 【sheep.ice】
一、前言
This article begins with graph theoryDijkstratopic arrangement,First, two templates will be sorted out,针对dijkstranaive and optimized versions,This series will also be updated all the time,Do related topics later,will be included in this topic!And for this algorithm,The general requirement is for some directed graphs,The minimum distance of different paths from one point to another end point,Note that the weight of the directed edge must be positive at this time!
二、题目汇总
①朴素版Dijkstra(ACwing 849)
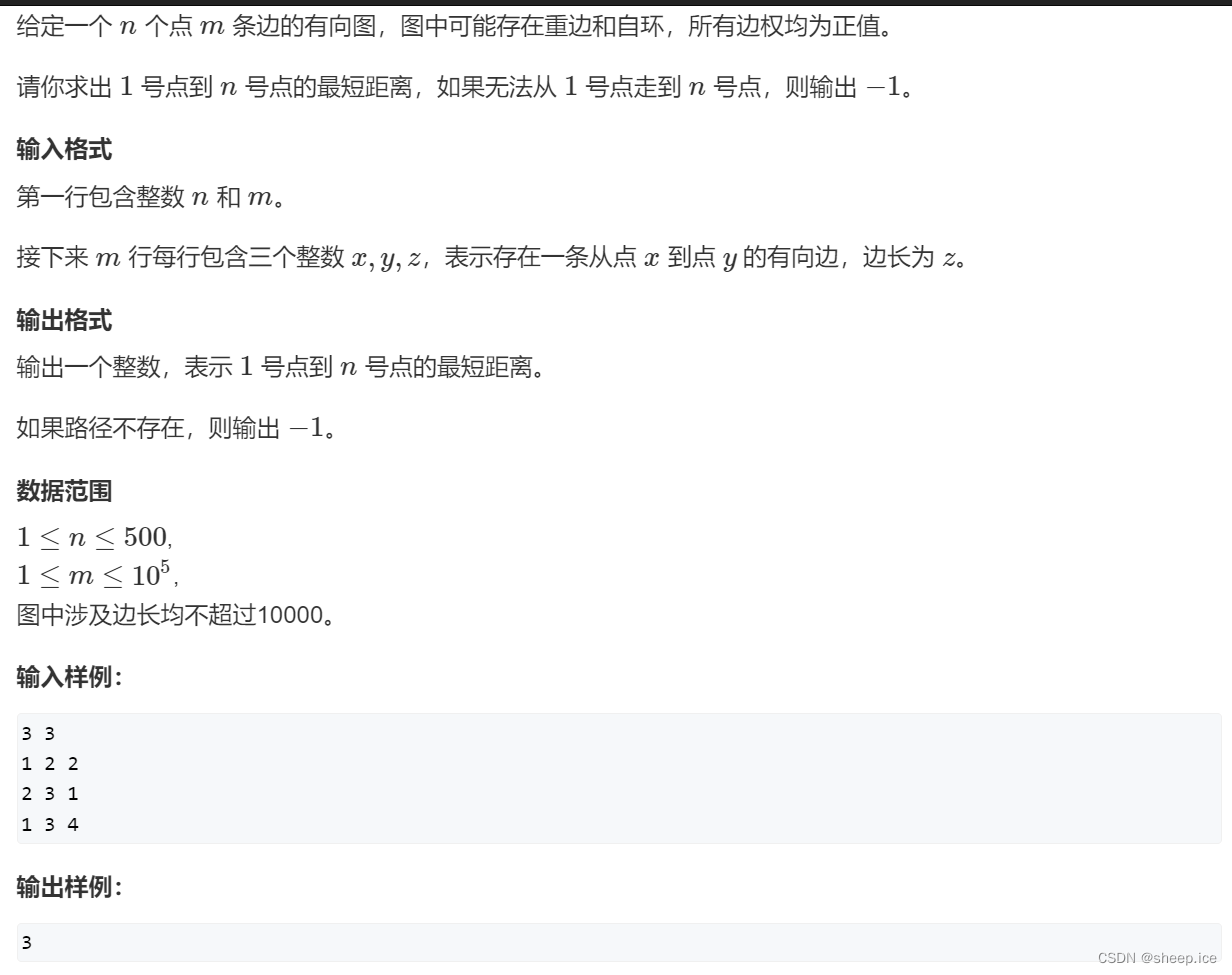
相关分析:
时间复杂度: O ( n 2 ) O(n^2) O(n2),此处的n代表点的数量
适用场景: The title is a dense graph,点比较少,But there are more sides.At this time, the adjacency matrix is used to store the graph!
思路: 朴素版本的DijkstraThe overall idea is that,从某个点(Mark it as point one)Start by setting its distance to 0,Then, the distance from other points to the first point is continuously updated through the point with a shorter distance from itself.The outer loop is the number of loop points,The inner loop is to find the first point closest to the origin,Then use that point to update the closest distance of his other edges to the origin.
完整AC代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 505;
//邻接矩阵存图, n表示点数,m表示边数量;
int g[N][N], n, m;
//distAn array representing the shortest distance from a point to the origin
int dist[N];
//Records whether a point has been updated
bool st[N];
void dijkstra() {
//The origin distance itself is 0
dist[1] = 0;
//两层循环
for(int i = 1; i <= n; i ++ ) {
//哨兵,Ease of selection
int t = -1;
//Find the point with the shortest distance from the origin that is not used to update other points
for(int j = 1; j <= n; j ++ ) {
if(!st[j] && (t == -1 || dist[j] < dist[t])) {
t = j;
}
}
//tThis point has already been used to update
st[t] = true;
//用tUpdate this point
for(int j = 1; j <= n; j ++ ) {
dist[j] = min(dist[j], g[t][j] + dist[t]);
}
}
}
int main() {
//初始化,At the beginning, both sides are positive infinity,Easy to take minimum,Determine if there is a path
memset(g, 0x3f, sizeof g);
memset(dist, 0x3f, sizeof dist);
cin >> n >> m;
for(int i = 1; i <= m; i ++ ) {
//代表a到b有一个权值为v的边
int a, b, v;
cin >> a >> b >> v;
//Self-loops can be ruled out in advance
if(a != b) g[a][b] = min(g[a][b], v);
}
//进行求解
dijkstra();
//如果路径不存在,那么dist[n]Still infinite
if(dist[n] == 0x3f3f3f3f) cout << -1 << endl;
else cout << dist[n] << endl;
return 0;
}
②堆优化版Dijkstra(ACwing.850)
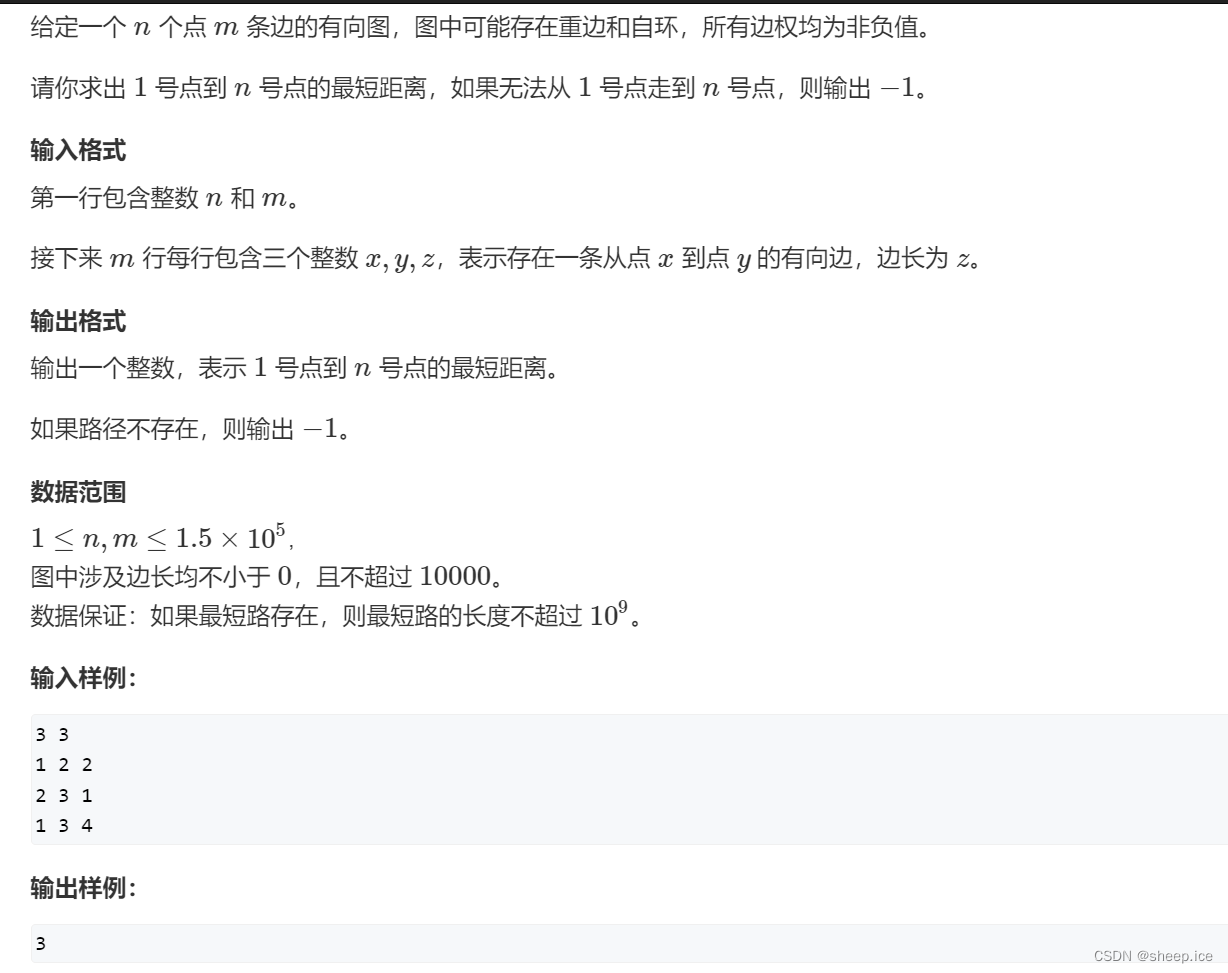
相关分析
时间复杂度: O ( m l o g m ) O(mlogm) O(mlogm)
适用场景: The biggest difference between this question and the first question is that the number of points has increased,And if used again O ( n 2 ) O(n^2) O(n2)will time out,So there are more points to watch,When the number of edges can meet the time complexity, it can be used.
思路: The reason for this optimization,Mainly because we can see the first solution and look for it againtWhen used to update other paths,It is guaranteed by using a layer of loops to updatetThe update distance of that point is the shortest,But in fact, this process can use a data structure–优先队列(堆)related optimizations,And the operation to do a lookup on the heap isO(1)的,Just after removing the element,adjust the heap,是需要log的时间,So the above time can be optimized.
完整AC代码
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#define x first
#define y second
using namespace std;
typedef pair<int, int> PII;
const int N = 2e5;
int m, n, dist[N];
//Use the adjacency list
int h[N], e[N], ne[N], w[N], idx;
//put one in the queuepair,pairThe first install distance,The second decoration number
//因为pairThe default is to sort by the first keyword
//In this way, the sorting can be done according to the short distance
priority_queue<PII, vector<PII>, greater<PII> > q;
bool st[N];
//Half of the adjacency list add operation,头插法
void add(int a, int b, int c) {
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++ ;
}
void dijkstra() {
dist[1] = 0;
//Let the queue exist at the first point first,第一个点的距离为0,编号是1
q.push({0, 1});
while(q.size()) {
auto t = q.top();
q.pop();
//If this point has been updated other points do not need to update
if(st[t.y]) continue;
//Mark this point to update other points
st[t.y] = true;
for(int i = h[t.y]; i != -1; i = ne[i]) {
int j = e[i];
//Only when the distance of a certain point can be updated
//Just put that point in the queue,May be used to update the distance of other points to the origin
if(dist[j] > w[i] + dist[t.y]) {
dist[j] = w[i] + dist[t.y];
q.push({dist[j], j});
}
}
}
}
int main() {
//初始化操作
//The distance is first initialized to positive infinity
//The head node starts to point to null,记作-1
memset(dist, 0x3f, sizeof dist);
memset(h, -1, sizeof h);
memset(st, 0, sizeof st);
cin >> n >> m;
for(int i = 1; i <= m; i ++ ) {
int a, b, c;
cin >> a >> b >> c;
add(a, b, c);
}
dijkstra();
if(dist[n] == 0x3f3f3f3f) cout << -1 << endl;
else cout << dist[n] << endl;
return 0;
}
边栏推荐
- PGSQL database to realize the import and export
- np.nan, np.isnan, None, pd.isnull, pd.isna finishing and summary
- Js scratchable latex style draw plug-in
- Taurus.MVC V3.0.3 Microservice Open Source Framework Released: Make the evolution of .NET architecture easier in large concurrency.
- 如何关闭开启硬件加速[通俗易懂]
- How to implement waterfall flow layout (what is waterfall flow layout)
- this的绑定指向详细解答
- How to better assess credit risk?Just watch this scorecard model live
- 机器人碰撞检测方法形式化
- Introduction to Graph Neural Networks (GNN) "Recommended Collection"
猜你喜欢
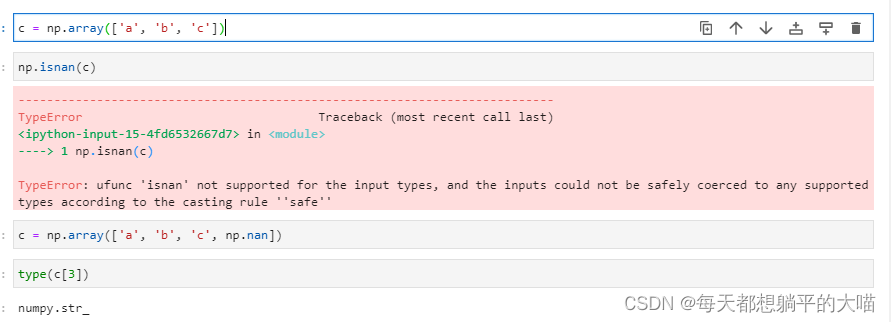
np.nan, np.isnan, None, pd.isnull, pd.isna finishing and summary

svg balloon rises explosion js special effect
js半圆环加载进度动画js特效
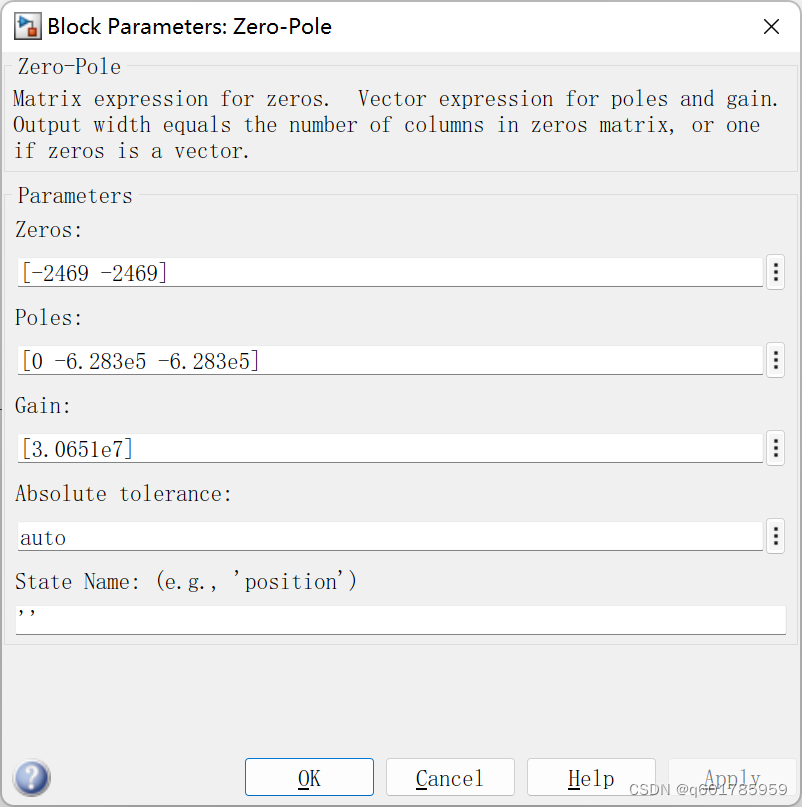
An example of type3 voltage loop compensator taking Boost as an example
Do you really understand the business process service BPass?
Custom mvc framework review
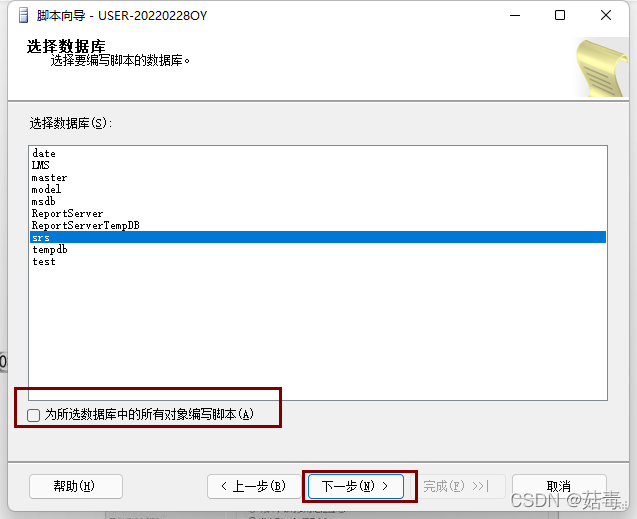
SQL Server database generation and execution of SQL scripts

Article 48 - Analysis of timestamp2 parameters【2022-08-01】
A powerful js pop-up alert plugin
js cool dashboard plugin
随机推荐
scrapy框架初识1
ssm access database data error
zabbix自动化监控脚本
工厂方法模式
SQL Server 2019 installation error 0 x80004005 service there is no timely response to the start or control request a detailed solution
Set proxy server (Google+IE) "Recommended Collection"
Data Lake (2): What is Hudi
Software component analysis: 5 major capabilities to protect software supply chain security
FreeRTOS creation tasks - dynamic creation, static creation
Pod Scheduling Strategy: Affinity, Stain and Stain Tolerance
SQL Server2019安装步骤及脱机安装Microsoft机器学习组件下一步不能继续的问题
Scala基础语法入门(三)Scala中的各种运算符
Drools(8): WorkBench uses
冰箱“扩容”的战事,在今夏格外猛烈
How to turn off hardware acceleration [easy to understand]
数据湖(二):什么是Hudi
RestTemplate 使用:设置请求头、请求体
pytorch模型转tensorflow模型
消除气泡解救蘑菇h5小游戏源码
How to use the database like tap water?|Tencent Cloud Database TDSQL-C