当前位置:网站首页>你知道图论的spfa吗?
你知道图论的spfa吗?
2022-08-02 12:49:00 【sheep.ice】
一、前言
对于之前有写到的Dijkstra算法,我们发现他只能用来计算边的权值为正的情况,这其实也就是为什么我们需要开一个st数组,对于一个已经被更新过的点来说,他一旦用于更新其他点的时候,我们就不需要再考虑再利用这个点再次更新其他的点。
但是呢,如果点之间的边是负值的时候,就必须去遍历一下所有的边,因为存在负值的时候,负数加正数是会把距离缩短的,所以呢就可以利用遍历所有边的办法去更新点到原点的距离。这就需要用到后续要说的spfa算法,那么在讲这个算法之前,需要了解bellman-ford算法,会先利用这个算法进行一个引入。
二、题目汇总
①bellman-ford(ACwing.853)

相关分析
时间复杂度: O ( m n ) O(mn) O(mn)
适用场景: 这个算法可以看到,时间复杂度比较高,所以mn的值要落在 1 e 7 − 1 e 8 1e7-1e8 1e7−1e8之间才能满足不超时,另外,由于这个算法,是从原点出发,外层循环多少次,内层就需要更新多少次边。这个实际含义就是,外层循环多少次,就代表:从原点出发了多少条边,所以能够计算,走多少条边到终点的一个最短距离,注意这个最短距离并不一定是整个图看上去的最短,而是满足了走k条边的最短!
思路: 如果题目规定走k条边,那么按照上述分析,外层循环k次代表走k条边的更新情况,内部循环,更新每一条边,一旦能够更新就更新,不能更新的话,距离保证不变。这里注意由于内层循环更新的是所有的边,所以是有可能发生应该只再原本的基础上衍生1条边,但是衍生出去了2条边。所以需要一个回溯的数组,保存一下上一次更新好的dist数组。而这个串联反应可以举个例子,如下:
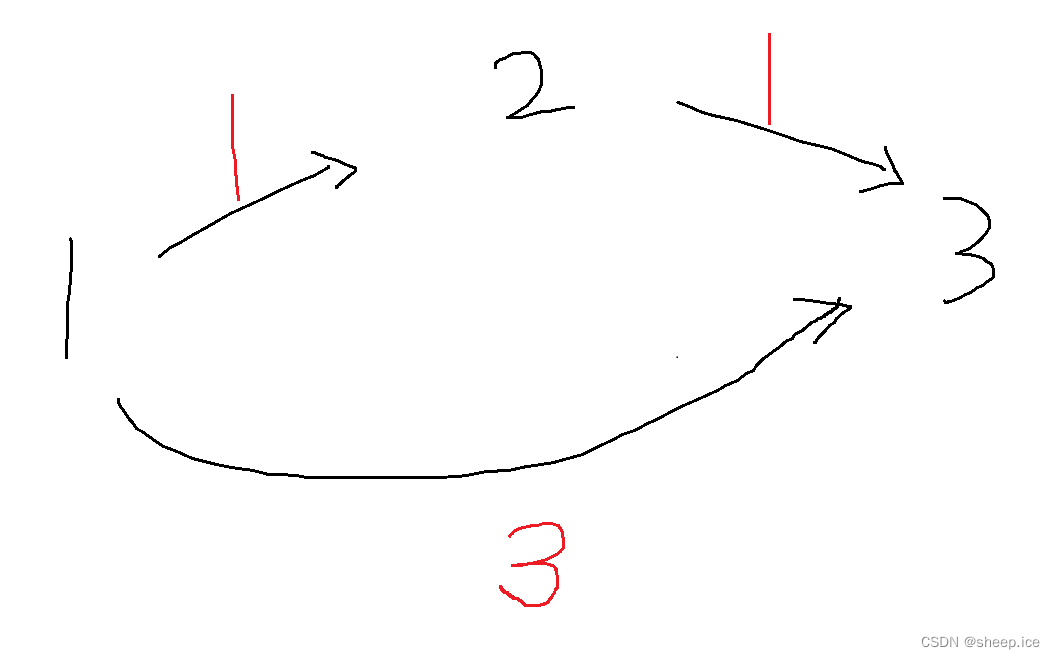
假设这个图,如果我们的k只给1的话,那么从1->3的距离最短应该为3,而不是1+1=2。假设我们在更新的时候,还是像之前dijkstra的更新方式,利用dist数组更新的话,那么在仅有的一次循环里面,1->2这条边的距离首先会被更新为1,那么在2->3这条边就会按照dist[2] = 1的这个数组更新dist[3],让dist[3]变成2,那么就和我们最终得到的答案3就是不同的。
完整AC代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 505, M = 10050;
//因为要遍历所有边,所以结构体存图
struct Edge {
int a, b, c;
}edges[M];
int dist[N], n, m, k;
//设置一个回溯的数组
int backup[N];
void bellman_ford() {
dist[1] = 0;
for(int i = 1; i <= k; i ++ ) {
//先进行一个备份操作
memcpy(backup, dist, sizeof dist);
for(int i = 1; i <= m; i ++ ) {
auto t = edges[i];
//就是这个地方,如果写成
//dist[t.b] > dist[t.a] + t.c的话
//就会有可能出现串联反应
if(dist[t.b] > backup[t.a] + t.c) {
dist[t.b] = backup[t.a] + t.c;
}
}
}
}
int main() {
cin >> n >> m >> k;
memset(dist, 0x3f, sizeof dist);
for(int i = 1; i <= m; i ++ ) {
int a, b, c;
cin >> a >> b >> c;
//代表a到b有一条权值为c的边
edges[i] = {a, b, c};
}
bellman_ford();
if(dist[n] > 0x3f3f3f3f / 2) cout << "impossible" << endl;
else cout << dist[n] << endl;
}
②spfa模板(ACwing.851)

相关分析
时间复杂度: O ( m ) O(m) O(m)
适用场景: 其实spfa这个算法以他比较优越的时间复杂度,其实用在很多题目都可以,且不仅能够求带负权的最短路,在一定程度上也可以解决dijkstra的题目。并且这个算法,可以判定一个图里面是否有负环
思路: 这里的思路其实也是从上一个bellman-ford算法延申过来的。我们可以看到,上一个算法的好处就是可以知道有边限制的最短路,但是其实如果没有边的限制的话,第一个算法其实在内层循环遍历边的时候,会有很多操作本身更新不了一个点到原点的距离,但是还是进行了一个尝试更新的操作。那么spfa的话其实就是可以排除这些没有实际价值的更新操作,也就是说在$dist[j] = dist[t] + w[i] $的那一步,只有一个点能够达到这一步操作了,让这个点进入队列之中,才有机会更新其他的边,如果某个点本身压根无法更新其他边,那也就没有必要让他到队列中再去更新其他边
完整AC代码
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 1e5 + 5;
bool st[N];
int dist[N], n, m;
int h[N], w[N], e[N], ne[N], idx;
queue<int> q;
void add(int a, int b, int c) {
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}
void spfa() {
q.push(1);
dist[1] = 0;
st[1] = true;
//利用类似宽搜的方法进行优化
while(q.size()) {
auto t = q.front();
q.pop();
//注意用过的点,有可能在后续更新的时候会继续用
st[t] = false;
for(int i = h[t]; i != -1; i = ne[i]) {
int j = e[i];
if(dist[j] > dist[t] + w[i]) {
dist[j] = dist[t] + w[i];
if(!st[j]) {
q.push(j);
st[j] = true;
}
}
}
}
}
int main() {
memset(h, -1, sizeof h);
memset(st, 0, sizeof st);
memset(dist, 0x3f, sizeof dist);
cin >> n >> m;
for(int i = 1; i <= m; i ++ ) {
int a, b, c;
cin >> a >> b >> c;
add(a, b, c);
}
spfa();
if(dist[n] > 0x3f3f3f3f / 2) cout << "impossible" << endl;
else cout << dist[n] << endl;
return 0;
}
代码相关问题
这里的话有一个问题,就是为什么一个已经被使用来更新其他点的点,从对头取出来的那一刻,他的st数组要被更新成为没有使用过,这里举一个例子,例子图如下:
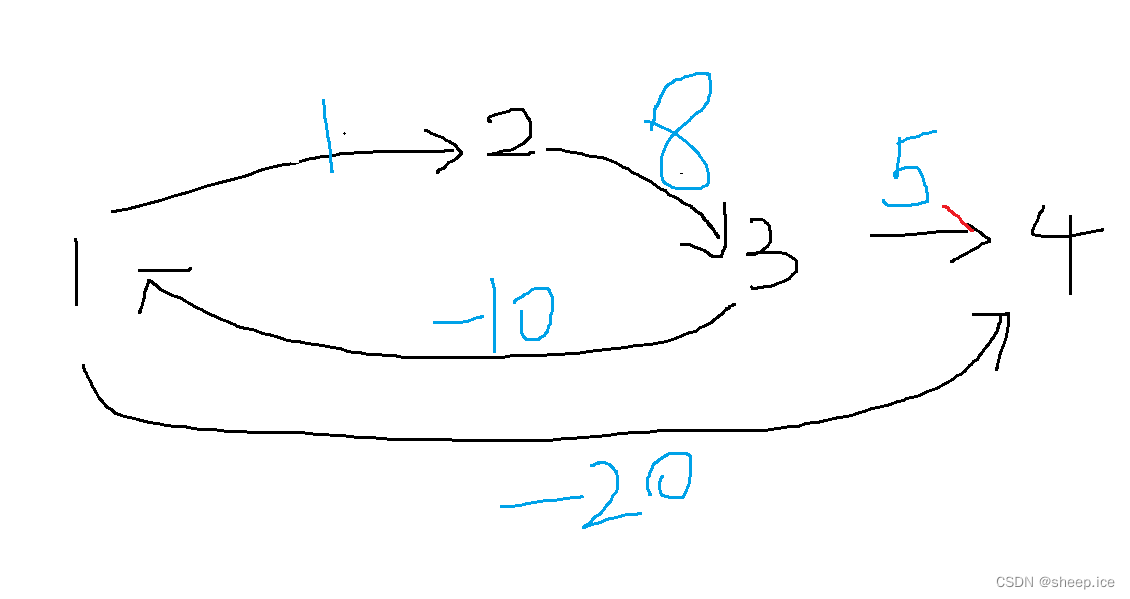
我们可以看到这个图,假设,我们在用1这个点第一次更新好1->2和1->4的距离后,不让他的st数组变为false的话,那么当3这个点用来更新1的时候,很显然从1->2->3->1一回会让整个路径变小,而我们虽然更新了一下3->1的距离,但是并没有在后面让1入队的话,那么1这个点就不会继续更新4这个点,当然这个例子有些问题,因为,我们可以一直让上方的环不断的走,让最后的1到4的路径距离不断的减少,所以希望读者有更好的例子可以举例一下。
当然,这个题,如果不专门用st代表是否访问,直接更新然后不断放点那其实就等同于bellman-ford算法了,所以还是建议这个地方能够继续好好理解一下。然后也正因为这样,spfa算法可以去判定一下是否有负环,或者是否有一个环可以让某一个路径的距离一直减小。
③spfa判断负环(ACwing. 852)
负环的定义就是一个环上边的权值全部为负数,刚开始我还一直这么认为的,其实负环应该是一个环上所有数加起来的权值和是为负数叫做负环,因此根据上面的一个分析,其实判断负环就很容易了,就看循环是不是一直跑不出来,因为不能死循环,所以我们要利用一个cnt数组,判断一下某个点走了多少次,根据抽屉原理,一旦走的次数比n大的时候,那么一定存在负环。
完整AC代码
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 100050, INF = 1e9 + 10;
int n, m, idx;
int h[N], e[N], ne[N], w[N];
int dist[N], cnt[N];
bool st[N];
void add(int a, int b, int c) {
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++ ;
}
bool spfa() {
queue<int> q;
for(int i = 1; i <= n; i ++ ) {
q.push(i);
st[i] = true;
}
while(q.size()) {
int t = q.front();
q.pop();
st[t] = false;
for(int i = h[t]; i != -1; i = ne[i] ) {
int j = e[i];
if(dist[j] > dist[t] + w[i]) {
dist[j] = dist[t] + w[i];
cnt[j] = cnt[t] + 1;
if(cnt[j] >= n) return true;
if(!st[j]) {
st[j] = true;
q.push(j);
}
}
}
}
return false;
}
int main() {
cin >> n >> m;
memset(h, -1, sizeof h);
for(int i = 0; i < m; i ++ ) {
int a, b, c;
cin >> a >> b >> c;
add(a, b, c);
}
if(spfa()) cout << "Yes" << endl;
else cout << "No" << endl;
return 0;
}
代码问题
为什么dist数组不用初始化为正无穷?
其实就是,负环必须走的那个路径是有负数产生的,且由于一个环必须满足权值为负,那么我们其实可以偷懒一下,让每次开始更新dist出现在,我们搜索的时候,第一次搜到的负数开始,然后在更新dist,如果有负环,那么这个dist是会不断减少的。这个等价于什么呢,我们可以发现,之前的题目都是从1这个点出发开始的,而负环不一定存在1这个点连接的路径上,所以其实在刚开始,队列就应该把所有点放进去,然后所有点去找负环,那也就是说从这个角度看,所有点距离本身的距离为0,那么初始化为0就是正确的!
边栏推荐
- 如何关闭开启硬件加速[通俗易懂]
- 企业用直播平台能实现什么
- Pod Scheduling Strategy: Affinity, Stain and Stain Tolerance
- Pod调度策略:亲和性、污点与污点容忍
- FreeRTOS experiment -- delete task
- Intelligent Image Analysis-Intelligent Home Appliance Image Target Detection Statistical Counting Detection and Recognition-iCREDIT
- Js scratchable latex style draw plug-in
- WPF——自定义日历
- Object.entries()
- Intouch System Platform IDE-1
猜你喜欢
Speed up your programs with bitwise operations
SQL Server 2019安装错误0x80004005 服务没有及时响应启动或控制请求详细解决方法
如何搭建威纶通触摸屏与S7-200smart之间无线PPI通信?

水平垂直居中方式

js九宫格样式抽奖插件
![PHP+MYSQL [Student Information Management System] (Minimalist Edition)](/img/86/d5d39eef0600acabbf3ac16c255c18.png)
PHP+MYSQL [Student Information Management System] (Minimalist Edition)

SQL Server 2019 installation error 0 x80004005 service there is no timely response to the start or control request a detailed solution
js炫酷仪表盘插件
np.nan, np.isnan, None, pd.isnull, pd.isna 整理与小结

svg实现的树木四季变化
随机推荐
第11章 文件
智能手表前景如何?
无线振弦采集仪远程修改参数方式
水平垂直居中方式
消除气泡解救蘑菇h5小游戏源码
js cool dashboard plugin
Import and export data of SQL Server database
np.nan, np.isnan, None, pd.isnull, pd.isna 整理与小结
3 ways for OpenFeign to set headers
Data Lake (2): What is Hudi
1.3 Rapid Spanning Tree Protocol RSTP
Basic protocol explanation
定了!2022世界VR产业大会将继续在南昌召开
php - the first of three solid foundations
30 lines of code to realize serverless real-time health code recognition -- operation manual
pig4cloud服务架构使用
手撸架构,Redis面试41问
Chapter 14 Manually create a REST service (2)
SQL Server 数据库之生成与执行 SQL 脚本
自定义mvc框架复习