当前位置:网站首页>C. Divan and bitwise operations
C. Divan and bitwise operations
2022-08-03 21:03:00 【秦小咩】
C. Divan and bitwise operations
time limit per test
1 second
memory limit per test
256 megabytes
input
standard input
output
standard output
Once Divan analyzed a sequence a1,a2,…,ana1,a2,…,an consisting of nn non-negative integers as follows. He considered each non-empty subsequence of the sequence aa, computed the bitwise XOR of its elements and added up all the XORs, obtaining the coziness of the sequence aa.
A sequence cc is a subsequence of a sequence dd if cc can be obtained from dd by deletion of several (possibly, zero or all) elements. For example, [1,2,3,4][1,2,3,4], [2,4][2,4], and [2][2] are subsequences of [1,2,3,4][1,2,3,4], but [4,3][4,3] and [0][0] are not.
Divan was very proud of his analysis, but now he lost the sequence aa, and also the coziness value! However, Divan remembers the value of bitwise OR on mm contiguous subsegments of the sequence aa. It turns out that each element of the original sequence is contained in at least one of these mm segments.
Divan asks you to help find the coziness of the sequence aa using the information he remembers. If several coziness values are possible, print any.
As the result can be very large, print the value modulo 109+7109+7.
Input
The first line contains one integer number tt (1≤t≤1031≤t≤103) — the number of test cases.
The first line of each test case contains two integer numbers nn and mm (1≤n,m≤2⋅1051≤n,m≤2⋅105) — the length of the sequence and the number of contiguous segments whose bitwise OR values Divan remembers, respectively.
The following mm lines describe the segments, one per line.
Each segment is described with three integers ll, rr, and xx (1≤l≤r≤n1≤l≤r≤n, 0≤x≤230−10≤x≤230−1) — the first and last elements of the segment and the bitwise OR of al,al+1,…,aral,al+1,…,ar, respectively.
It is guaranteed that each element of the sequence is contained in at least one of the segments. It is guaranteed that there exists a sequence that satisfies all constraints.
It is guaranteed that the sum of nn and the sum of mm over all test cases do not exceed 2⋅1052⋅105.
Output
For each test case print the coziness any suitable sequence aa modulo 109+7109+7.
Example
input
Copy
3 2 1 1 2 2 3 2 1 3 5 2 3 5 5 4 1 2 7 3 3 7 4 4 0 4 5 2
output
Copy
4 20 112
Note
In first example, one of the sequences that fits the constraints is [0,2][0,2]. Consider all its non-empty subsequences:
- [0][0]: the bitwise XOR of this subsequence is 00;
- [2][2]: the bitwise XOR of this subsequence is 22;
- [0,2][0,2]: the bitwise XOR of this subsequence is 22.
The sum of all results is 44, so it is the answer.
In second example, one of the sequences that fits the constraints is [0,5,5][0,5,5].
In third example, one of the sequences that fits the constraints is [5,6,7,0,2][5,6,7,0,2].
=========================================================================
我们把各区间异或和给|起来,虽然会有交叉,但|不会算重复,只会取一个并集,并集也就是a1^a2.....an
这样我们就构造了一个带求解数列的异或和,还是考虑每一个位置,因为要求每一个子段的异或和,不妨对n个数的每个二进制位单独考虑.
第p位 二进制大小为 2^(p-1) 设有k个1,n-k个0, 我们想产生 2^(p-1)的贡献,就必须选择奇数个1,
若k为奇数,选法为 2^(k-1)种, n为偶数也是2^(k-1)种,0的话,选几个都行 2^(n-k)种,共计
2^(n-1)种
当然这是在p位置至少有1个1的情况下的结论,我们异或出来伪原数列这一位如果是1,那么n个数里面一定至少一个1,如果是0,可以有很多1,但是我们把它当成没有1即可。
那么答案就是求出来伪原数列,求出不全是0的二进制位即可。
# include <iostream>
# include<algorithm>
# include<cstring>
# include<vector>
# include<queue>
# define mod 1000000007
using namespace std;
typedef long long int ll;
ll qp(ll base, ll pow)
{
ll ans=1;
while(pow)
{
if(pow&1)
ans=ans*base%mod;
pow>>=1;
base=base*base%mod;
}
return ans;
}
int main()
{
ll t;
cin>>t;
while(t--)
{
ll n,k;
cin>>n>>k;
ll sum=0;
for(int i=1;i<=k;i++)
{
ll l,r,x;
cin>>l>>r>>x;
sum|=x;
}
ll ans=0,temp=qp(2ll,n-1);
for(int i=0;i<=30;i++)
{
if((sum&(1ll<<i)))
{
ans+=(1ll<<i)*temp;
ans%=mod;
}
}
cout<<ans<<endl;
}
return 0;
}
边栏推荐
猜你喜欢
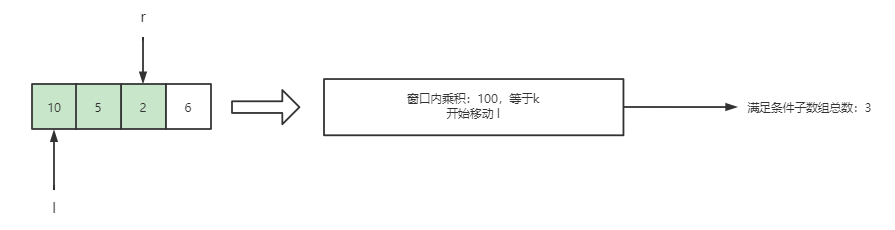
通关剑指 Offer——剑指 Offer II 009. 乘积小于 K 的子数组
CC2530_ZigBee+华为云IOT:设计一套属于自己的冷链采集系统

NAACL 2022 | 具有元重加权的鲁棒自增强命名实体识别技术

Several difficult problems in DDD

Power button 206 - reverse list - the list
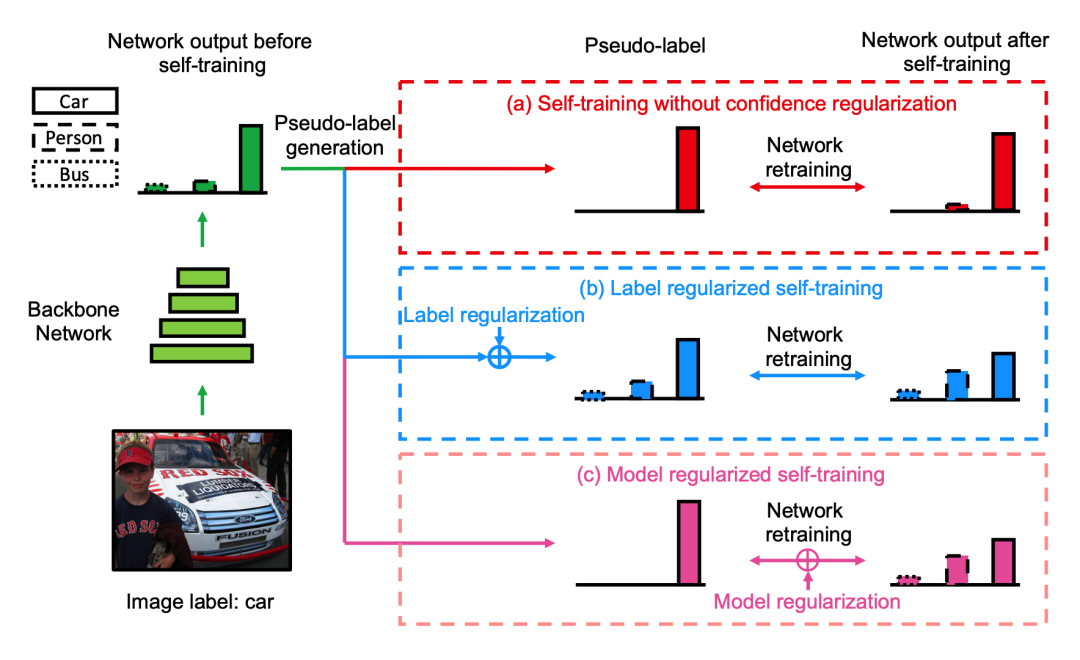
False label aggregation

DDD 中的几个困难问题
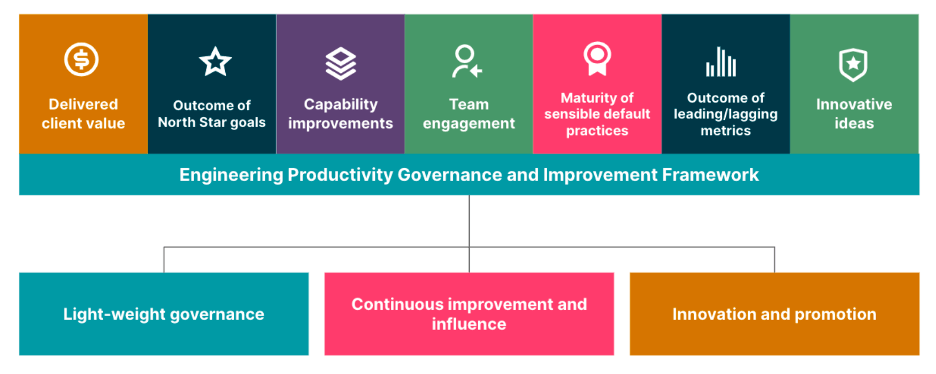
Engineering Effectiveness Governance for Agile Delivery
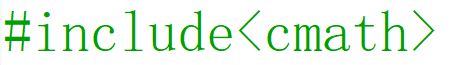
abs()、fabs() 和 labs() 的区别
【HiFlow】经常忘记签到怎么办?使用腾讯云场景连接器每天提醒你。
随机推荐
伪标签汇总
leetcode refers to Offer 58 - II. Left Rotate String
敏捷交付的工程效能治理
leetcode 231. Powers of 2
Leetcode 899. An orderly queue
3种圆形按钮悬浮和点击事件
Often forget HiFlow 】 【 check-in?Use tencent cloud scenario connector to remind you every day.
Leetcode 16. Numerical integral power (power + fast recursive/iteration)
Leetcode 125. Verify palindrome string
LeetCode_Digit Statistics_Medium_400. Nth Digit
ES6--residual parameters
ES6 deconstruction assignment - array object deconstruction and deconstruction
tidyverse based on data.table?
回忆三年浮沉
leetcode 326. 3 的幂
Markdown语法
idea2021配置svn报错Cannot run program “svn“ (in directory “xxx“):CreateProcess error=2,系统找不到指定的文件
XSS线上靶场---haozi
业界新标杆!阿里开源自研高并发编程核心笔记(2022 最新版)
Abs (), fabs () and LABS ()