当前位置:网站首页>树和二叉树
树和二叉树
2022-07-22 20:43:00 【快乐不能半途而废】
目录
一、树的简单认识
定义
树(tree)是 n(n ≥ 0)个节点的有限集合,当n = 0时,为空树;当n > 0 时,为非空树。人以一棵非空树,满足以下两个条件:
1)有且仅有一个称为根的节点;
2)除根节点以外,其余节点可以分为m( m > 0 )个互不相交的有限集 ,期中每一个集合本身又是一棵树,并且称为根的子树(subtree)。
,期中每一个集合本身又是一棵树,并且称为根的子树(subtree)。

与树相关的术语比较多:
● 节点——节点包含数据元素及若干指向子树的分支信息。
● 节点的度——节点拥有的子树个数。
● 树的度——树中节点的最大度数。
● 终端节点——度为0的节点,又称为叶子。
● 分支节点——度大于0的节点。除了叶子都是分支节点。
● 内部节点——除了树根和叶子都是内部节点。
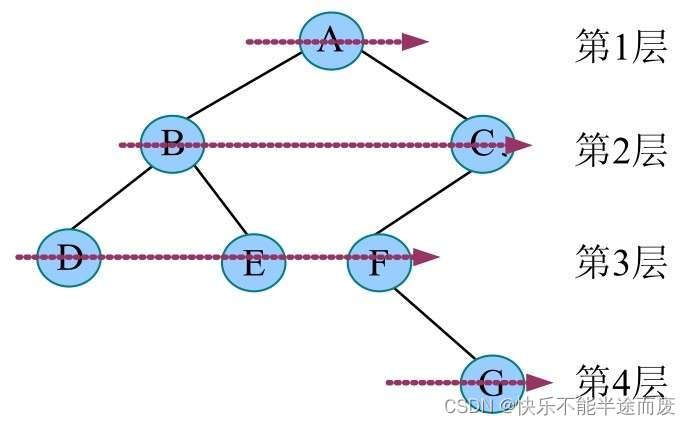
● 节点的层次——从根到该节点的层数(根节点为第1层)。
● 树的深度(或高度)——指所有节点中最大的层数● 路径——树中两个节点之间所经过的节点序列。
● 路径长度——两节点之间路径上经过的边数。● 双亲、孩子——节点的子树的根称为该节点的孩子,反之,该节点为其孩子的双亲。
● 兄弟——双亲相同的节点互称兄弟。
● 堂兄弟——双亲是兄弟的节点互称堂兄弟。
● 祖先——从该节点到树根经过的所有节点称为该节点的祖先。
● 子孙——节点的子树中的所有节点都称为该节点的子孙。
二、二叉树
2.1 定义
二叉树(binary tree)是n(n≥0)个节点构成的集合,它或为空树(n=0),或满足以下两个条件:
1)有且仅有一个称为根的节点;
2)除根节点以外,其余节点分为两个互不相交的子集 和
和 ,分别称为T的左子树和右子树,且
,分别称为T的左子树和右子树,且 和
和 本身都是二叉树。
本身都是二叉树。

二叉树是一种特殊的树,它最多有两个子树,分别为左子树和右子树,二者是有序的,不可以互换。也就是说,二叉树中不存在度大于2的节点。
2.2二叉树的基本性质
性质一:二叉树的第  层上最多有
层上最多有  个节点(
个节点( ≥ 1)
≥ 1)
性质二:一棵深度为k的二叉树中,最多有 个结点,最少有k个结点
个结点,最少有k个结点
性质三:在一棵二叉树中,如果叶子结点数为 ,度为2的结点数为
,度为2的结点数为 ,则有:
,则有:  =
= +1。
+1。
性质四:具有n个结点的完全二叉树的深度为  。
。
2.3二叉树的l链式存储和遍历
(1)二叉链表:令二叉树的每个结点对应一个链表结点,链表结点除了存放与二叉树结点有关的数据信息外,还要设置指示左右孩子的指针。

template<class T>
struct Binode
{
T data;//通用数据类型
Binode<T>* lchild, * rchild;
};
(2)二叉链表的创建:从二叉树的定义可以看出,它是递归定义的(除了根之外,左,右子树也是一棵二叉树),因此可以用递归来创建二叉树。下面将介绍的是补空法:
补空法:补空法是指如果左子树或右子树为空时,则用特殊字符补空,如“#”,然后按照根、左子树、右子树的顺序,得到先序遍历序列,根据该序列递归创建二叉树。
算法思路:
1)输入补空后的二叉树先序遍历序列。
2)如果ch=='#', bt=NULL;否则创建一个新节点bt,令bt->data=ch;递归创建T的左子树;递归创建T的右子树。图解:
二叉树补空之后的先序遍历是:ABD##E##CF#G###
代码实现:(使用了模板)
Binode<T>* creat(Binode<T>* bt) { T ch; cin >> ch; if (ch == '#') bt = NULL; else { bt = new Binode<T>; bt->data = ch; //生成根节点 bt->lchild = creat(bt->lchild);//递归创建左孩子 bt->rchild = creat(bt->rchild);//递归创建右孩子 } return bt; }
(3)二叉树的遍历:
二叉树的遍历就是按照某条路径搜索访问二叉树中的节点一次且仅访问一次,遍历是有顺序的,我们首先考虑二叉树的结构,按照根D,左子树L和右子树R的访问先后顺序不同有六种访问方式。如果限定先访问左子树再访问右子树,则只有三种遍历方式:先序遍历(DLR),中序遍历(LRD),后序遍历(LRD)。因为树本身是递归定义的,因此树的基本操作用递归算法比较容易实现。
先序遍历算法:
1)访问根节点;
2)先序遍历左子树;
3)先序遍历右子树。图示:
代码实现:
void Preorder(Binode<T>* bt) {//前序遍历 if (bt != NULL) { cout << bt->data << " "; Preorder(bt->lchild); Preorder(bt->rchild); } }
中序遍历算法:
1)中序遍历左子树;
2)访问根节点;
3)中序遍历右子树。图示:
代码:
void Inorder(Binode<T>* bt) {//中序遍历 if (bt != NULL) { Inorder(bt->lchild); cout << bt->data << " "; Inorder(bt->rchild); } }后序遍历算法:
1)后序遍历左子树;
2)后序遍历右子树;
3)访问根节点。图示:
代码:
void Postorder(Binode<T>* bt) {//后序遍历 if (bt != NULL) { Postorder(bt->lchild); Postorder(bt->rchild); cout << bt->data << " "; } }
由观察可知以上三种遍历不同之处是根节点访问位置不同,那么代码上的区别就是 “cout << bt->data << " "; ”语句所在的位置不同。
(4)层序遍历
二叉树的遍历除一般的先序遍历、中序遍历和后序遍历这3种遍历之外,还有另一种遍历方式——层次遍历,即按照层次的顺序从左向右进行遍历。
遍历过程:
( A )——(B C)——( D E F )—— ( G )
观察可得结论:一对括号作为一组, 每一组遍历是上一组所有节点的孩子,按照先左孩子再右孩子的顺序,那么我们如何实现? 这时候通常使用的是队列。
访问根节点A ,A入队
取队首元素 A ,A左右孩子不为空依次入队,并将A出队,队列元素:B C
取队首元素 B ,B左右孩子不为空依次入队,并将B出队,队列元素:C D E
取队首元素 C ,C左孩子不为空入队,并将C出队,队列元素: D E F
取队首元素 D ,D的左右孩子为空,无元素入队,将D出队,队列元素: E F
……
什么时候结束呢?答案当然是:队列元素数量为0的时候啦
那废话不多说了:代码代码
void Levelorder(Binode<T>* bt)
{//层序遍历
Binode<T>* temp = NULL;
queue<Binode<T>*>LeQue;
LeQue.push(bt);//入队根节点
while (!LeQue.empty())
{
temp = LeQue.front();
cout << temp->data << " ";
LeQue.pop();//队首元素出队
if (temp->lchild != NULL)
LeQue.push(temp->lchild);/左孩子不为空,左孩子入队
if (temp->rchild != NULL)
LeQue.push(temp->rchild);//右孩子不为空,右孩子入队
}
}思考:如何利用层序遍历思路实现找到二叉树的最大宽度呢?(是我想偷懒了)
2.4二叉树的顺序存储和遍历
(1) 顺序存储:二叉树的顺序存储结构就是用一维数组存储二叉树中的结点,并且结点的存储位置(下标)应能体现结点之间的逻辑关系——父子关系。

普通二叉树在顺序结构存储时,需要补充成为完全二叉树,在对应完全二叉树没有孩子的位置补充 “ ^ ” ,再进行标号。根节点对应编号1,编号后我们会发现,左孩子(L)和右孩子(R)的标号与双亲节点标号(P)之间的关系:L = 2*P,R = 2*P +1;
数组下标

(2)在得到顺序存储的一维数组后,我们也来实现一下二叉树的一些基本操作:
遍历:与链式存储结构遍历的算法思路相同,只不过是将在链表上的操作转化成为在数组上实现。我们已知,前序遍历:根节点->左孩子->右孩子 ,中序遍历:左孩子->根节点->右孩子 ,后序遍历:右孩子 - >左孩子->根节点。
在遍历的算法思路不变的情况下,我们要如何做才能实现这三种遍历呢?回看链式存储时候的代码,我们发现关键的代码就在于递归访问时参数(也就是左孩子和右孩子的表示)的变化,换到这里就是找到在数组中左右孩子的表示方法。那不就是……那不就是……L = 2*P,R = 2*P +1
void PreOreder(int v)
{//前序遍历
if (arr[v] != '^')
{
cout << arr[v] << " ";
PreOreder(2 * v);
PreOreder(2 * v + 1);
}
}
void InOrder(int v)
{//中序遍历
if (arr[v] != '^')
{
InOrder(2 * v);
cout << arr[v] << " ";
InOrder(2 * v + 1);
}
}
void PosOrder(int v)
{//后序遍历
if (arr[v] != '^')
{
PosOrder(2 * v);
PosOrder(2 * v + 1);
cout << arr[v] << " ";
}
}是不是很简单哇 ^_^
那重要的问题来了——在知道基本的算法思路之后我们该如何通过给定的二叉树得到顺序结构存储的数组呢?(具体操作见代码注释叭)----------偷懒中----------
//存储下标和结构体节点
template<class T>
struct StoreN
{
Binode<T>* Node_1;
int index;
};
//主要代码
template<class T>
void Bitree<T>::ProInorder(Binode<T>* bt)
{
StoreN<T>* item = new StoreN<T>;
int j = 0;//初始化顺序数组
for (j = 0; j < Maxn; j++)
arr[j] = '^';
queue<StoreN<T>*> Q;//用于寻找记录下标
int i = 1;
arr[i] = bt->data;//记录根节点的数据
item->Node_1 = bt;
item->index = i;//记录根节点对应的下标
Q.push(item);
while (Q.empty() != 1)
{
item = Q.front();
Q.pop();//记得出队,不然陷入循环了
if (item->Node_1->lchild != NULL)//如果左孩子不为空
{
StoreN<T>* templ = new StoreN<T>;//用于左孩子,一定要定义在里面
templ->index = 2 * item->index; //存储左孩子在数组中的下标
templ->Node_1 = item->Node_1->lchild; //存储左孩子节点
arr[templ->index] = templ->Node_1->data; //找到左孩子在数组中的位置
Q.push(templ);
}
if (item->Node_1->rchild != NULL)//如果右孩子不为空
{
StoreN<T>* tempr = new StoreN<T>;//用于右孩子
tempr->index = 2 * item->index + 1;
tempr->Node_1 = item->Node_1->rchild;
arr[tempr->index] = tempr->Node_1->data;
Q.push(tempr);
}
}
arr[item->index + 1] = '\0'; //输出得到的一维数组
cout << arr + 1 << "\n";
}2.5二叉树的深度
链式:
int GetBTdepth(Binode<T>* bt)
{
int leftC = 0, rightC = 0;
if (bt != NULL)
{
leftC = GetBTdepth(bt->lchild) + 1;
rightC = GetBTdepth(bt->rchild) + 1;
}
return leftC > rightC ? leftC : rightC;
}顺序结构:
int GetBTdepth(int v)
{
int leftC = 0, rightC = 0;
if (arr[v] != '^')
{
leftC = GetBTdepth(2*v) + 1;
rightC = GetBTdepth(2*v+1) + 1;
}
return leftC > rightC ? leftC : rightC;
}存储完整代码:
#include<iostream>
#include<iomanip>
#include<cstdio>
#include<queue>
using namespace std;
const int Maxn = 102;
char arr[Maxn] = { 0 };//顺序结构存储
template<class T>
struct Binode
{
T data;
Binode<T>* lchild, * rchild;
};
template<class T>
struct StoreN
{
Binode<T>* Node_1;
int index;
};
template<class T>
class Bitree
{
private:
Binode<T>* root = NULL;
Binode<T>* creat(Binode<T>* bt)
{
T ch;
cin >> ch;
if (ch == '#')
bt = NULL;
else
{
bt = new Binode<T>;
bt->data = ch;
bt->lchild = creat(bt->lchild);
bt->rchild = creat(bt->rchild);
}
return bt;
}
void release(Binode<T>* bt)
{
if (bt != NULL)
{
release(bt->lchild);
release(bt->rchild);
cout << bt->data << "节点被删除" << "\n";
delete bt;
}
}
void Preorder(Binode<T>* bt)
{//前序遍历
if (bt != NULL)
{
cout << bt->data << " ";
Preorder(bt->lchild);
Preorder(bt->rchild);
}
}
void Inorder(Binode<T>* bt)
{//中序遍历
if (bt != NULL)
{
Inorder(bt->lchild);
cout << bt->data << " ";
Inorder(bt->rchild);
}
}
void Postorder(Binode<T>* bt)
{//后序遍历
if (bt != NULL)
{
Postorder(bt->lchild);
Postorder(bt->rchild);
cout << bt->data << " ";
}
}
void Levelorder(Binode<T>* bt)
{//层序遍历
Binode<T>* temp = NULL;
queue<Binode<T>*>LeQue;
LeQue.push(bt);
while (!LeQue.empty())
{
temp = LeQue.front();
cout << temp->data << " ";
LeQue.pop();
if (temp->lchild != NULL)
LeQue.push(temp->lchild);
if (temp->rchild != NULL)
LeQue.push(temp->rchild);
}
}
int MaxBTwidth(Binode<T>* bt)
{
//求树的最大宽度
Binode<T> *temp = NULL;
int w = 0;
int i = 0;
queue<Binode<T>*>Que;
Que.push(bt);
w = 1;
int maxw = w;
while (!Que.empty())
{
temp = Que.front();
for (i = 0; i < w; i++)
{
if (temp->lchild != NULL)
Que.push(temp->lchild);
if (temp->rchild != NULL)
Que.push(temp->rchild);
Que.pop();
}
w = Que.size();
if (maxw < w)
maxw = w;
}
return maxw;
}
int GetBTdepth(Binode<T>* bt)
{
int leftC = 0, rightC = 0;
if (bt != NULL)
{
leftC = GetBTdepth(bt->lchild) + 1;
rightC = GetBTdepth(bt->rchild) + 1;
}
return leftC > rightC ? leftC : rightC;
}
void GetSortArr(Binode<T>*bt);
public:
Bitree() { root = creat(root); }
~Bitree() { release(root); }
void Preorder() { Preorder(root); }
void Inorder() { Inorder(root); }
void Postorder() { Postorder(root); }
void Levelorder() { Levelorder(root); }
void GetSortArr() { GetSortArr(root); }
int MaxBTwidth() { return MaxBTwidth(root); }
int GetBTdepth() { return GetBTdepth(root); }
int DepthNodes(int item);
};
template<class T>
int Bitree<T>::DepthNodes(int item)
{
int count = 0;
int i = pow(2, item - 1);
int len = pow(2, item);
for (; i < len; i++)
{
if (arr[i] != '^')
{
cout << arr[i] << " ";
count++;
}
if (arr[i] == '\0')
return count;
}
return count;
}
template<class T>
void Bitree<T>::GetSortArr(Binode<T> *bt)
{
StoreN<T>* item = new StoreN<T>;
int j = 0;
for (j = 0; j < Maxn; j++)
arr[j] = '^';
queue<StoreN<T>*> Q;
int i = 1;
arr[i] = bt->data;
item->Node_1 = bt;
item->index = i;
Q.push(item);
while (Q.empty() != 1)
{
item = Q.front();
Q.pop();//记得出队,不然陷入循环了
if (item->Node_1->lchild != NULL)//如果左孩子不为空
{
StoreN<T>* templ = new StoreN<T>;
templ->index = 2 * item->index;
templ->Node_1 = item->Node_1->lchild;
arr[templ->index] = templ->Node_1->data;
Q.push(templ);
}
if (item->Node_1->rchild != NULL)//如果右孩子不为空
{
StoreN<T>* tempr = new StoreN<T>;
tempr->index = 2 * item->index + 1;
tempr->Node_1 = item->Node_1->rchild;
arr[tempr->index] = tempr->Node_1->data;
Q.push(tempr);
}
}
arr[item->index + 1] = '\0';
cout << arr + 1 << "\n";
}
int main()
{
Bitree<char>tree1;
tree1.GetSortArr();
cout << "\n前序遍历的结果是:\n";
tree1.Preorder();
cout << "\n中序遍历的结果是:\n";
tree1.Inorder();
cout << "\n后序遍历的结果是:\n";
tree1.Postorder();
cout << "\n层序遍历的结果是:\n";
tree1.Levelorder();
cout << "\n二叉树最大宽度是:";
cout << tree1.MaxBTwidth() ;
cout << "\n二叉树的深度为:";
int BTdepth = tree1.GetBTdepth();
cout << BTdepth << "\n";
int v;
cout << "你想要知道的哪一层节点:(请输入一个小于" << BTdepth << "的数)";//如果添加循环语句的话可以实现层序遍历>_>
cout << "层节点详情是:";
cin >> v;
cout << "层节点数目是: " << tree1.DepthNodes(v)<<"\n";
return 0;
}
<总结的时候改自己的bug实在是不易,如果有错误,还望指正,转载请声明,感谢阅读>
边栏推荐
- Redis五大基本数据类型的基本命令
- LAN SDN technology hard core insider - 3 prequel breaks through the bottleneck of multi-core virtualization
- GNU pseudo instruction definition function
- 程序员45岁之后,绝大部分都被淘汰吗?真相寒了众人的心
- Flutter memory leak detection
- Google cloud and Oracle cloud are "hot"? It is imperative to deploy cross cloud disaster recovery!
- 小程序毕设作品之微信酒店预订小程序毕业设计(5)任务书
- tensorflow2.0稀疏矩阵输入操作
- 现货白银走势图大致是怎么样变化的?
- 如何使用订单流分析工具(下)
猜你喜欢
随机推荐
编写一个具有搜索提示的搜索框
Digital collections start the 100 billion level market
Codeforces Round #808 (Div. 2) A - D
你的 NFT 会消失吗?DFINITY 提供 NFT 存储最佳方案
Electronic bidding procurement mall system: optimize traditional procurement business and speed up enterprise digital upgrading
【ARC127F】±AB
小程序毕设作品之微信校园二手书交易小程序毕业设计成品(2)小程序功能
使用Flutter与贝塞尔曲线画一个波浪球
C language file operation (including all knowledge points, detailed explanation of related functions and codes)
小程序毕设作品之微信校园二手书交易小程序毕业设计成品(6)开题答辩PPT
用于图像语义分割的GAU与PPM
ES6新增的class类
LAN SDN technology hard core insider - 3 prequel breaks through the bottleneck of multi-core virtualization
LAN SDN technology hard core insider - what's in the prequel CPU?
VR panoramic zoo, a zoo business card with different achievements
小程序毕设作品之微信酒店预订小程序毕业设计(8)毕业设计论文模板
One dimensional array and object array in [c # array]-c #
10个Live Demo都展示了啥?看过没看过的都值得再看一遍
ES6解决异步问题
LAN SDN technology hard core insider 13 II from LAN to Internet







![[ssm] unified result encapsulation](/img/ff/9528a062d464acee52047598af40c3.png)




