当前位置:网站首页>【Paper】2019_ Consensus Control of Multiple AUVs Recovery System Under Switching Topologies and Time D
【Paper】2019_ Consensus Control of Multiple AUVs Recovery System Under Switching Topologies and Time D
2022-06-30 04:35:00 【Zhao-Jichao】
link :【Paper】2017_ Research on coordinated control method of underwater vehicle formation marine survey
List of articles
I. INTRODUCTION
II. PROBLEM FORMULATION
A. GRAPH THEORY
B. THE AUV MODEL
combination Eq.(2.7) Sum formula (2.8), available AUV A feedback linearized dynamic model in standard second-order integral form :
x ˙ i = v i v ˙ i = u i (2.9) \begin{aligned} \dot{x}_i = v_i \\ \dot{v}_i = u_i \\ \end{aligned} \tag{2.9} x˙i=viv˙i=ui(2.9)
among , x i ∈ R 5 , v i ∈ R 5 , u i ∈ R 5 x_i \in \R^5, v_i \in \R^5, u_i \in \R^5 xi∈R5,vi∈R5,ui∈R5.
C. LEMMA
III. CONSENSUS CONTROL UNDER SWITCHING TOPOLOGIES AND TIME DELAYS
As mentioned earlier , Next, we will introduce the switching topology and the multi - node scheme with time delay AUV Restore the consistency control algorithm of the system . Mother ship and many AUV Run in the form of random switching topology . Suppose the interconnection topology is Markov switching , Markov chain describing switching process has a stationary probability distribution . Since the graph is allowed to be time-varying , We assume that there is M M M Two possible different graphs , The network topology switches between them .
A. DESIGN PROCEDURE
In this section , Many assumptions AUV The consensus control algorithm of the recovery system can ensure that all members reach the common motion state and expectation point . The mother ship is considered to be all AUV The point that must be pursued , Multiple AUV The recovery problem of can also be regarded as the consensus problem of multi member systems .
Definition 1
In a AUV In a system composed of , The first i i i individual AUV In time t t t The motion state vector of is x i ( t ) x_i(t) xi(t), The motion state of the mother ship is x m ( t ) x_m(t) xm(t). If the system satisfies the following formula , The recycling system can achieve consistency , And guarantee that AUV Be able to follow the mother ship continuously and stably .
lim t → ∞ = ∥ x i ( t ) − x m ( t ) ∥ = 0 \lim_{t\rightarrow \infty} = \| x_i(t) - x_m(t) \| = 0 t→∞lim=∥xi(t)−xm(t)∥=0
According to dynamics (2.9), The consistency algorithm considering mother ship dynamics is
x ˙ m ( t ) = v m ( t ) \dot{x}_{m}(t) = v_m(t) x˙m(t)=vm(t)
Define a group of independent topologies auv The dynamics of is as follows :
x ˙ i ( t ) = v i ( t ) v ˙ i ( t ) = u i ( t ) \begin{aligned} \dot{x}_i(t) = v_i(t) \\ \dot{v}_i(t) = u_i(t) \\ \end{aligned} x˙i(t)=vi(t)v˙i(t)=ui(t)
Consider a reason for AUV Composed of many AUV Recycling system , Each one AUV Treat as a directed graph G G G One of the nodes in , Utilization (2.9) in AUV Standard dual integrator dynamics , Based on the consensus algorithm, the following consensus control can be designed :
Define a group of independent topologies auv The dynamics of is as follows :
u i ( t ) = − K ∑ j ∈ N i a i j ( t ) ( ( p i ( t ) − p j ( t ) ) + ( v i ( t ) − v j ( t ) ) ) − K c i ( t ) ( ( p i ( t ) − p m ( t ) ) + ( v i ( t ) − v m ( t ) ) ) (3.1) \begin{aligned} u_i(t) = &-K \sum_{j\in N_i} a_{ij}(t) (~(\red{p_i(t)} - \green{p_j(t)}) + (\red{v_i(t)}-\green{v_j(t)})~) \\ &-K c_i(t) (~(\red{p_i(t)} - \blue{p_m(t)}) + (\red{v_i(t)}-\blue{v_m(t)})~) \\ \end{aligned} \tag{3.1} ui(t)=−Kj∈Ni∑aij(t)( (pi(t)−pj(t))+(vi(t)−vj(t)) )−Kci(t)( (pi(t)−pm(t))+(vi(t)−vm(t)) )(3.1)
Due to limited communication , It is easy to cause delay . A consensus algorithm with delay is given
u i ( t ) = − K ∑ j ∈ N i a i j ( t ) ( ( p i ( t − τ 1 ) − p j ( t − τ 1 − τ 2 ) ) + ( v i ( t − τ 1 ) − v j ( t − τ 1 − τ 2 ) ) ) − K c i ( t ) ( ( p i ( t − τ 1 ) − p m ( t ) ) + ( v i ( t − τ 1 ) − v m ( t ) ) ) (3.2) \begin{aligned} u_i(t) = &-K \sum_{j\in N_i} a_{ij}(t) (~(\red{p_i(t-\tau_1)} - \green{p_j(t-\tau_1-\tau_2)}) + (\red{v_i(t-\tau_1)}-\green{v_j(t-\tau_1-\tau_2)})~) \\ &-K c_i(t) (~(\red{p_i(t-\tau_1)} - \blue{p_m(t)}) + (\red{v_i(t-\tau_1)}-\blue{v_m(t)})~) \\ \end{aligned} \tag{3.2} ui(t)=−Kj∈Ni∑aij(t)( (pi(t−τ1)−pj(t−τ1−τ2))+(vi(t−τ1)−vj(t−τ1−τ2)) )−Kci(t)( (pi(t−τ1)−pm(t))+(vi(t−τ1)−vm(t)) )(3.2)
u i u_i ui: Is the control input
K K K: Yes protocol gain
p i ∈ R n p_i \in \R^n pi∈Rn: Is the position state
v i ∈ R n v_i \in \R^n vi∈Rn: Is the speed state
p m ∈ R n p_m \in \R^n pm∈Rn: Is the mother ship position status
v m ∈ R n v_m \in \R^n vm∈Rn: Is the speed status of the mother ship
a i j ( t ) a_{ij}(t) aij(t): Communication weight
c m ( t ) c_{m}(t) cm(t): Communication weight with mother ship
C = diag { c 1 , c 2 , ⋯ , c N } C = \text{diag}\{c_1, c_2, \cdots, c_N\} C=diag{ c1,c2,⋯,cN}
τ 1 , τ 2 ( t ) \tau_1, \tau_2(t) τ1,τ2(t): Respectively represent the input ( Constant ) And communication weights ( Time varying in the interval )
Mother ship and the i i i individual AUV The status of is
x m ( t ) = [ p m T ( t ) v m T ( t ) ] T ∈ R 10 n x i ( t ) = [ p i T ( t ) v i T ( t ) ] T ∈ R 10 n \begin{aligned} x_m(t) = \left[\begin{matrix} p^\text{T}_m(t) & v^\text{T}_m(t) \end{matrix}\right]^\text{T} \in \R^{10n} \\ x_i(t) = \left[\begin{matrix} p^\text{T}_i(t) & v^\text{T}_i(t) \end{matrix}\right]^\text{T} \in \R^{10n} \\ \end{aligned} xm(t)=[pmT(t)vmT(t)]T∈R10nxi(t)=[piT(t)viT(t)]T∈R10n
The above recovery problem is transformed into an error analysis problem , Definition No i i i individual AUV The system state error vector relative to the motion state information of the Mothership is
ε i ( t ) = x i ( t ) − x m ( t ) \varepsilon_i(t) = x_i(t) - x_m(t) εi(t)=xi(t)−xm(t)
Definition
ε ( t ) = ( ε 1 T ( t ) , ε 2 T ( t ) , ⋯ , ε N T ( t ) ) T \varepsilon(t) = (\varepsilon_1^\text{T}(t), \varepsilon_2^\text{T}(t), \cdots, \varepsilon_N^\text{T}(t))^\text{T} ε(t)=(ε1T(t),ε2T(t),⋯,εNT(t))T,
ε ( t ) = [ ε p T ( t ) ε v T ( t ) ] T \varepsilon(t) = \left[\begin{matrix} \varepsilon^\text{T}_p(t) & \varepsilon^\text{T}_v(t) \end{matrix}\right]^\text{T} ε(t)=[εpT(t)εvT(t)]T
here
ε p ( t ) , ε v ( t ) \varepsilon_p(t), \varepsilon_v(t) εp(t),εv(t) Respectively represent the error of position state and speed state .
Then the system can be transformed into the following matrix form
ε ˙ ( t ) = ( I n ⊗ A ) ε ( t ) − B ⊗ K ε ( t − τ 1 ) + C ⊗ K ε ( t − μ ) (3.3) \dot{\varepsilon}(t) = (I_n \otimes A) ~\varepsilon(t) - B \otimes K ~\varepsilon(t-\tau_1) + C \otimes K ~\varepsilon(t-\mu) \tag{3.3} ε˙(t)=(In⊗A) ε(t)−B⊗K ε(t−τ1)+C⊗K ε(t−μ)(3.3)
The original formula is as follows , But there's a problem , The revised ones are as follows :
ε ˙ ( t ) = ( I n ⊗ A ) ε ( t ) − ( I n ⊗ K i B ) ε ( t − τ 1 ) + ( I n ⊗ K i C ) ε ( t − μ ) (3.3) \dot{\varepsilon}(t) = (I_n \otimes A) ~\varepsilon(t) - (I_n\otimes K_i B) ~\varepsilon(t-\tau_1) + (I_n \otimes K_i C) ~\varepsilon(t-\mu) \tag{3.3} ε˙(t)=(In⊗A) ε(t)−(In⊗KiB) ε(t−τ1)+(In⊗KiC) ε(t−μ)(3.3)
here
μ = τ 1 + τ 2 \mu = \tau_1 + \tau_2 μ=τ1+τ2
A = [ 0 I 0 0 ] ∈ R 10 × 10 A = \left[\begin{matrix} 0 & I \\ 0 & 0 \\ \end{matrix}\right] \in \R^{10 \times 10} A=[00I0]∈R10×10
B = [ 0 0 D + C D + C ] ∈ R 10 × 10 B = \left[\begin{matrix} 0 & 0 \\ \mathcal{D} + \mathcal{C} & \mathcal{D} + \mathcal{C} \\ \end{matrix}\right] \in \R^{10 \times 10} B=[0D+C0D+C]∈R10×10
C = [ 0 0 A A ] ∈ R 10 × 10 C = \left[\begin{matrix} 0 & 0 \\ \mathcal{A} & \mathcal{A} \\ \end{matrix}\right] \in \R^{10 \times 10} C=[0A0A]∈R10×10
A = [ a i j ] ∈ R 5 × 5 \mathcal{A} = \left[\begin{matrix} a_{ij} \end{matrix}\right] \in \R^{5 \times 5} A=[aij]∈R5×5
C = diag { c 1 , c 2 , ⋯ , c N } ∈ R 5 × 5 \mathcal{C} = \text{diag}\{c_1, c_2, \cdots, c_N\} \in \R^{5 \times 5} C=diag{ c1,c2,⋯,cN}∈R5×5
D = diag { ∑ j ∈ N 1 a 1 j , ∑ j ∈ N 2 a 2 j , ⋯ , ∑ j ∈ N N a N j } ∈ R 5 × 5 \mathcal{D} = \text{diag}\{\sum_{j\in N_1}a_{1j}, \sum_{j\in N_2}a_{2j}, \cdots, \sum_{j\in N_N}a_{Nj}\} \in \R^{5 \times 5} D=diag{ ∑j∈N1a1j,∑j∈N2a2j,⋯,∑j∈NNaNj}∈R5×5
Expand it for easy understanding :
ε ˙ 1 ( t ) = A ε 1 − K i B ε 1 + K i C ε 1 = [ 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ] [ p 1 x − p m x p 1 y − p m y p 1 z − p m z p 1 θ − p m θ p 1 ψ − p m ψ v 1 u − v m u v 1 v − v m v v 1 w − v m w v 1 q − v m q v 1 r − v m r ] − K i [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 c 1 + d 1 0 0 0 0 c 1 + d 1 0 0 0 0 0 c 2 + d 2 0 0 0 0 c 2 + d 2 0 0 0 0 0 c 3 + d 3 0 0 0 0 c 3 + d 3 0 0 0 0 0 c 4 + d 4 0 0 0 0 c 4 + d 4 0 0 0 0 0 c 5 + d 5 0 0 0 0 c 5 + d 5 ] [ p 1 x − p m x p 1 y − p m y p 1 z − p m z p 1 θ − p m θ p 1 ψ − p m ψ v 1 u − v m u v 1 v − v m v v 1 w − v m w v 1 q − v m q v 1 r − v m r ] + K i [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 a 12 a 13 a 14 a 15 0 a 12 a 13 a 14 a 15 a 21 0 a 23 a 24 a 25 a 21 0 a 23 a 24 a 25 a 31 a 32 0 a 34 a 35 a 31 a 32 0 a 34 a 35 a 41 a 42 a 43 0 a 45 a 41 a 42 a 43 0 a 45 a 51 a 52 a 53 a 54 0 a 51 a 52 a 53 a 54 0 ] [ p 1 x − p m x p 1 y − p m y p 1 z − p m z p 1 θ − p m θ p 1 ψ − p m ψ v 1 u − v m u v 1 v − v m v v 1 w − v m w v 1 q − v m q v 1 r − v m r ] \begin{aligned} \dot{\varepsilon}_1(t) &= A \varepsilon_1 - K_i B \varepsilon_1 + K_i C \varepsilon_1 \\ &= \left[\begin{matrix} 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{matrix}\right] \left[\begin{matrix} p^x_1 - p^x_m \\ p^y_1 - p^y_m \\ p^z_1 - p^z_m \\ p^\theta_1 - p^\theta_m \\ p^\psi_1 - p^\psi_m \\ \\ v^u_1 - v^u_m \\ v^v_1 - v^v_m \\ v^w_1 - v^w_m \\ v^q_1 - v^q_m \\ v^r_1 - v^r_m \\ \end{matrix}\right] \\ &-K_i \left[\begin{matrix} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \\ c_1+d_1 & 0 & 0 & 0 & 0 & c_1+d_1 & 0 & 0 & 0 & 0 \\ 0 & c_2+d_2 & 0 & 0 & 0 & 0 & c_2+d_2 & 0 & 0 & 0 \\ 0 & 0 & c_3+d_3 & 0 & 0 & 0 & 0 & c_3+d_3 & 0 & 0 \\ 0 & 0 & 0 & c_4+d_4 & 0 & 0 & 0 & 0 & c_4+d_4 & 0 \\ 0 & 0 & 0 & 0 & c_5+d_5 & 0 & 0 & 0 & 0 & c_5+d_5 \\ \end{matrix}\right] \left[\begin{matrix} p^x_1 - p^x_m \\ p^y_1 - p^y_m \\ p^z_1 - p^z_m \\ p^\theta_1 - p^\theta_m \\ p^\psi_1 - p^\psi_m \\ \\ v^u_1 - v^u_m \\ v^v_1 - v^v_m \\ v^w_1 - v^w_m \\ v^q_1 - v^q_m \\ v^r_1 - v^r_m \\ \end{matrix}\right] \\ &+K_i \left[\begin{matrix} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \\ 0 & a_{12} & a_{13} & a_{14} & a_{15} & 0 & a_{12} & a_{13} & a_{14} & a_{15} \\ a_{21} & 0 & a_{23} & a_{24} & a_{25} & a_{21} & 0 & a_{23} & a_{24} & a_{25} \\ a_{31} & a_{32} & 0 & a_{34} & a_{35} & a_{31} & a_{32} & 0 & a_{34} & a_{35} \\ a_{41} & a_{42} & a_{43} & 0 & a_{45} & a_{41} & a_{42} & a_{43} & 0 & a_{45} \\ a_{51} & a_{52} & a_{53} & a_{54} & 0 & a_{51} & a_{52} & a_{53} & a_{54} & 0 \\ \end{matrix}\right] \left[\begin{matrix} p^x_1 - p^x_m \\ p^y_1 - p^y_m \\ p^z_1 - p^z_m \\ p^\theta_1 - p^\theta_m \\ p^\psi_1 - p^\psi_m \\ \\ v^u_1 - v^u_m \\ v^v_1 - v^v_m \\ v^w_1 - v^w_m \\ v^q_1 - v^q_m \\ v^r_1 - v^r_m \\ \end{matrix}\right] \end{aligned} ε˙1(t)=Aε1−KiBε1+KiCε1=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡0000000000000000000000000000000000000000000000000010000000000100000000001000000000010000000000100000⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡p1x−pmxp1y−pmyp1z−pmzp1θ−pmθp1ψ−pmψv1u−vmuv1v−vmvv1w−vmwv1q−vmqv1r−vmr⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤−Ki⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡00000c1+d10000000000c2+d20000000000c3+d30000000000c4+d40000000000c5+d500000c1+d10000000000c2+d20000000000c3+d30000000000c4+d40000000000c5+d5⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡p1x−pmxp1y−pmyp1z−pmzp1θ−pmθp1ψ−pmψv1u−vmuv1v−vmvv1w−vmwv1q−vmqv1r−vmr⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤+Ki⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡000000a21a31a41a5100000a120a32a42a5200000a13a230a43a5300000a14a24a340a5400000a15a25a35a450000000a21a31a41a5100000a120a32a42a5200000a13a230a43a5300000a14a24a340a5400000a15a25a35a450⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡p1x−pmxp1y−pmyp1z−pmzp1θ−pmθp1ψ−pmψv1u−vmuv1v−vmvv1w−vmwv1q−vmqv1r−vmr⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤
x ˙ 1 ( t ) − x ˙ m ( t ) = A ε − B ε + C ε \dot{x}_1(t) - \dot{x}_m(t) = A \varepsilon - B \varepsilon + C \varepsilon x˙1(t)−x˙m(t)=Aε−Bε+Cε
Mother ship and many auv Run as a random switching topology . This paper gives the common probability space of all random variables ( Ω , F , P ) (\Omega,\mathcal{F}, \mathcal{P}) (Ω,F,P), Ω \Omega Ω Is the space for basic events , F \mathcal{F} F Is in Ω \Omega Ω On the potential σ σ σ- site , P \mathcal{P} P yes F \mathcal{F} F Probability measure on .
In this paper, we consider using consistency algorithm (3.3) And Markov switching interconnection topology
ε ˙ ( t ) = ( I n ⊗ A ) ε ( t ) − B ( ρ t ) ⊗ K ( ρ t ) ε ( t − τ 1 ) + C ( ρ t ) ⊗ K ( ρ t ) ε ( t − μ ) (3.4) \dot{\varepsilon}(t) = (I_n \otimes A) ~\varepsilon(t) - \red{B(\rho_t)} \otimes \red{K(\rho_t)} ~\varepsilon(t-\tau_1) + \red{C(\rho_t)} \otimes \red{K(\rho_t)} ~\varepsilon(t-\mu) \tag{3.4} ε˙(t)=(In⊗A) ε(t)−B(ρt)⊗K(ρt) ε(t−τ1)+C(ρt)⊗K(ρt) ε(t−μ)(3.4)
System (3.4) Is a multiple with Markov switching topology and time delay AUVs Restore system consistency control , It reflects the mother ship and AUVs Between or AUVs Random communication process between . Communication is described by Markov random process , ρ t \rho_t ρt Is defined as a Markov process , In state space M = { 1 , 2 , ⋅ , M } \mathbb{M} = \{1, 2, \cdot , \mathbf{M} \} M={ 1,2,⋅,M} The inner value is . matrix B ( ρ t ) B(\rho_t) B(ρt) and C ( ρ t ) C(\rho_t) C(ρt) Random change from one mode to another by Markov jump process , The control gain changes from one mode to another in a Markov switching topology . Protocol gain K ( ρ t ) K(\rho_t) K(ρt) To ensure the consensus of the recovery system .
B. CONVERGENCE ANALYSIS
IV. NUMERICAL EXAMPLES

This is using the topology diagram (a) The simulation results
Through the speed state , It can be concluded that there is something wrong with the result in the original text 
This is the result of modifying the topology
I feel that there is not only a problem with the result in the original text , And there are problems with the communication topology 
边栏推荐
- Blocking queue example
- FortiGate firewall quick initialization administrator password
- One interview question a day the difference between B tree and b+ tree
- QT creator 8 beta2 release
- 史上最全的Redis基础+进阶项目实战总结笔记
- Five methods to clear floating and their advantages and disadvantages
- SSL update method
- IO stream, byte stream read / write copy
- The subsystem implementing transaction persistence in DBMS is ()
- Detailed explanation of cookies and sessions
猜你喜欢

What is an optocoupler circuit and what should be paid attention to in actual use?

Bean creation process and lazy init delay loading mechanism

Learn about threads

Bean创建流程 与 lazy-init 延迟加载机制原理

Break through the existing customer group marketing, and try customer grouping management (including clustering model and other practical effect evaluation)

Intern method of string
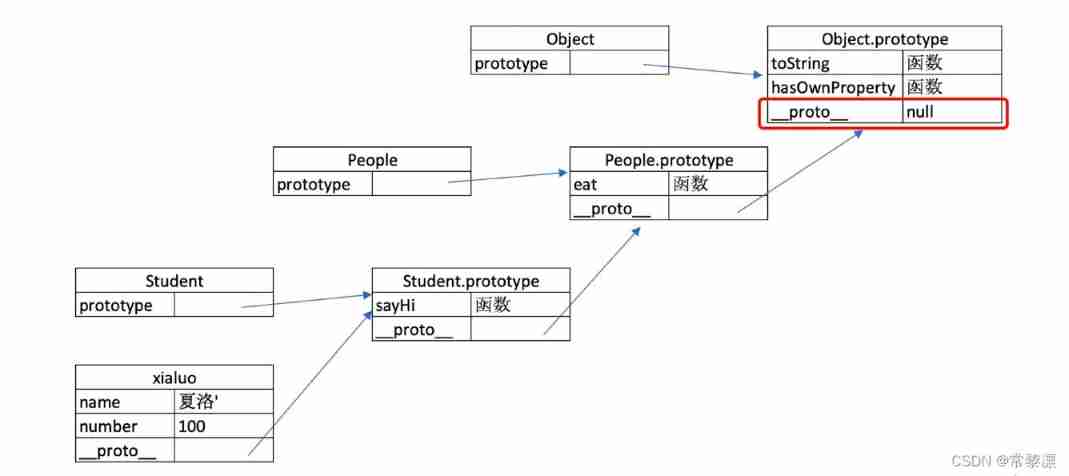
Junior students summarize JS basic interview questions

Cheap SSL certificate abroad

深度融合云平台,对象存储界的“学霸”ObjectScale来了

Foreign SSL certificate
随机推荐
Share an example of a simple MapReduce method using a virtual machine
Explain the underlying principles of JVM garbage collection in simple terms
JS import and export
OneNote production schedule
How to renew an SSL certificate
Requirements for transfer transaction cases: 1 Employee 1 transfers money to employee 2. Therefore, two update sals should be executed. Purpose: either both updates are successful or both implementati
Es2016 key summary
Threadlocal
Difference between request forwarding and redirection
Transport layer protocol tcp/udp
The subsystem implementing transaction persistence in DBMS is ()
System programming summary
oslo_ config. cfg. ConfigFileParseError: Failed to parse /etc/glance/glance-api. Conf: a solution to errors
Method of applying for code signing certificate by enterprise
OneNote software
The same node code will cause duplicate data
Refers to the difference between IP and *ip at output
Internship: interface case implementation
SSL universal domain name certificate
Geotrustov wildcard