Chow-Liu Tree

0.引言

• 基础概念参考
• 论文：Approximating discrete probability distributions with dependence trees

we consider the problem of best approximating an nth-order distribution by a product of n - 1 second-order distributions.

The Chow–Liu method describes a joint probability distribution $P(X_1,X_2,\dots ,X_n)$ as a product of second-order conditional and marginal distributions. For example, the six-dimensional distribution $P(X_1,X_2,X_3,X_4,X_5,X_6)$ might be approximated as

$$P^{\prime }(X_1,X_2,X_3,X_4,X_5,X_6)=P(X_6|X_5)P(X_5|X_2)P(X_4|X_2)P(X_3|X_2)P(X_2|X_1)P(X_1)$$

1.互信息 mutual information

将 互信息 视为边的权重。

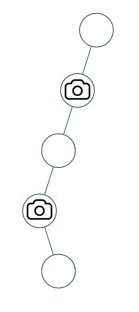
2.Chow-Liu Tree 理论基础

Given a joint PDF $P(x)$, the $KL$-divergence $D\left(P,P^{\prime }\right)$ is minimized by projecting $\mathrm{P}(\mathrm{x})$ on a maximum-weight spanning tree (MSWT) over nodes in $\mathrm{X}$, where the weight on the edge $\left(X_i,X_j\right)$ is defined by the mutual information measure
$$I\left(X_i;X_j\right)=\sum _{x_i,x_j}P\left(x_i,x_j\right)\log \frac{P\left(x_i,x_j\right)}{P\left(x_i\right)P\left(x_j\right)}$$

• 变换后的树与原树具有最小的Kullback-Leible散度。

3.Chow-Liu Tree 算法流程

• 对于分布 $P(x)$,对于所有的 $i\ne j$,计算联合分布 $P(X_i,Y_j)$;
• 使用第1步得到的概率分布,计算任意两个结点的互信息 $I(X_i,Y_j)$ ,并把 $I(X_i,Y_j)$ 作为这两个结点连接边的权值;
• 计算最大权生成树(Maximum-weight spanning tree)
  • a. 初始状态:n个变量(结点),0条边
  • b. 插入最大权重的边
  • c. 找到下一个最大的边,并且加入到树中;要求加入后,没有环生成。否则,查找次大的边;
  • d. 重复上述过程c过程直到插入了n-1条边(树建立完成)
• 选择任意结点作为根,从根到叶子标识边的方向;
• 该生成树的近似联合概率 $P^{\prime }(x)$ 和原贝叶斯网络的联合概率 $P(x)$ 的相对熵最小。

实际上算法操作流程和最小生成树是一样的，代表算法有 kruskal 与 prim 算法。

4.最小生成树

• 最小生成树

• 图的四大算法

• 最小生成树代码

5.半朴素贝叶斯分类器

• 摘抄自周志华老师《机器学习》（西瓜书）7.4.半朴素贝叶斯分类器.

---

半朴素贝叶斯分类器的基本想法是适当考虑一部分属性问的相互依赖信息，从而既不需进行完全联合概率计算，又不至于彻底忽略了比较强的属性依赖关系。“独依赖估计” (One-Dependent Estimator ,简称 ODE) 是半朴素贝叶斯分类器最常用的一种策略。顾名思议，所谓"独依赖"就是假设每个属性在类别之外最多仅依赖于一个其他属性，即
$$P(c\mid \mathbf{x})\propto P(c)\prod _{i=1}^{d}P\left(x_i\mid c,p{a}_i\right)$$
其中 $p{a}_i$ 为属性 $x_i$ 所依赖的属性, 称为 $x_i$ 的父属性. 此时, 对每个属性 $x_i$, 若 其父属性 $p{a}_i$ 已知, 则可采用类似式 $(7.20)$ 的办法来估计概率值 $P\left(x_i\mid c,p{a}_i\right)$. 于是, 问题的关键就转化为如何确定每个属性的父属性, 不同的做法产生不同的独依赖分类器。最直接的做法是假设所有属性都依赖于同一个属性,称为"超父 "(super-parent) ,然后通过交叉验证等模型选择方法来确定超父属性,由此形成了SPODE (Super-Parent ODE) 方法.例如,在图 7.1(b) 中, $x_1$ 是超父属性.

TAN (Tree Augmented naïve Bayes) [Friedman et al., 1997] 则是在最大带权生成树(maximum weighted spanning tree)算法 (Chow-Liu tree)[Chow and Liu, 1968] 的基础上, 通过以下步骤将属性间依赖关系约简为如图 $7.1(\mathrm{c})$ 所示的树形结构:

• (1) 计算任意两个属性之间的条件互信息 (conditional mutual information)
  $$I\left(x_i,x_j\mid y\right)=\sum _{x_i,x_j;c\in \mathcal{Y}}P\left(x_i,x_j\mid c\right)\log \frac{P\left(x_i,x_j\mid c\right)}{P\left(x_i\mid c\right)P\left(x_j\mid c\right)}$$
• (2) 以属性为结点构建完全图, 任意两个结点之间边的权重设为 $I\left(x_i,x_j\mid y\right)$
• (3) 构建此完全图的最大带权生成树, 挑选根变量, 将边置为有向;
• (4) 加入类别结点 $y$, 增加从 $y$ 到每个属性的有向边.

容易看出, 条件互信息 $I\left(x_i,x_j\mid y\right)$ 刻画了属性 $x_i$ 和 $x_j$ 在已知类别情况下的相关性, 因此, 通过最大生成树算法, $\mathrm{T}\mathrm{A}\mathrm{N}$ 实际上仅保留了强相关属性之间 的依赖性.

---