当前位置:网站首页>【学习笔记】主成分分析法介绍
【学习笔记】主成分分析法介绍
2022-06-28 19:59:00 【Burger叮当】
一:简介
主成分分析是用降维的方法将多指标转化为几个综合指标的多元统计分析方法,使用较少的变量去解释原来资料中的大部分信息。
二:基本原理和步骤
1.基本原理:略。
需要注意的是:
(1)主成分分析法结果受量纲的影响,需要先进行无量纲化处理,然后用协方差或相关系数矩阵进行分析。
(2)实际研究中选取的主成分不超过6个,只需要贡献率超过85%即可。
2.基本步骤:

三:例题

#程序文件Pex11_7.py
import numpy as np
from sklearn.decomposition import PCA
a=np.loadtxt("Pdata11_7.txt")
b=np.r_[a[:,1:4],a[:,-3:]] #构造数据矩阵
# #np.r_是按列连接两个矩阵,就是把两矩阵上下相加,要求列数相等。‘
#所以上面构造矩阵的方法研究一下就明白了。
md=PCA().fit(b) #构造并训练模型
print("特征值为:",md.explained_variance_)
print("各主成分的贡献率:",md.explained_variance_ratio_)
print("奇异值为:",md.singular_values_)
print("各主成分的系数:\n",md.components_) #每行是一个主成分
"""下面直接计算特征值和特征向量,和库函数进行对比"""
cf=np.cov(b.T) #计算协方差阵
c,d=np.linalg.eig(cf) #求特征值和特征向量
print("特征值为:",c)
print("特征向量为:\n",d)
print("各主成分的贡献率为:",c/np.sum(c)) 
如上所示:使用库函数PV=CA时,主成分正负号不可控,因此我们直接计算特征值和特征向量。
同时:PCA使用协方差矩阵进行主成分分析。我们也可以选用相关系数阵。这样相当于对数据进行了标准化处理。
四:主成分分析的应用
用于综合评价的一般步骤:

例11.8
#程序文件Pex11_8.py
import numpy as np
from scipy.stats import zscore
a=np.loadtxt("Pdata11_8.txt")
print("相关系数阵为:\n",np.corrcoef(a.T))
b=np.delete(a,0,axis=1) #删除第1列数据
#这是因为r12=r21=1,所以x1,x2完全线性相关,选取指标一致,只保留一个即可
c=zscore(b); r=np.corrcoef(c.T) #数据标准化并计算相关系数阵
d,e=np.linalg.eig(r) #求特征值和特征向量
rate=d/d.sum() #计算各主成分的贡献率
print("特征值为:",d)
print("特征向量为:\n",e)
print("各主成分的贡献率为:",rate)
k=1; #提出主成分的个数
F=e[:,:k]; score_mat=c.dot(F) #计算主成分得分矩阵
score1=score_mat.dot(rate[0:k]) #计算各评价对象的得分
score2=-score1 #通过观测,调整得分的正负号
#这里主要是因为前面特征向量没有取相反数。如果取了这里就不用取反
print("各评价对象的得分为:",score2)
index=score1.argsort()+1 #排序后的每个元素在原数组中的位置
print("从高到低各个城市的编号排序为:",index)这里注意:先观察相关系数阵,如果有非对角线元素为1,则说明变量选取不合理,二者完全线性相关,应删除一个指标。

注意:关于主成分得分矩阵以及评价对象得分,详见下图。因为本题为效益型指标值,所以评价值越大排名越高。否则排名取反即可。

边栏推荐
猜你喜欢

On the first anniversary of the data security law, which four major changes are coming?

easypoi
如何获取飞机穿过雷达两端的坐标
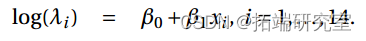
R语言GLM广义线性模型:逻辑回归、泊松回归拟合小鼠临床试验数据(剂量和反应)示例和自测题

Why is it not enough to declare the structure alias when using the structure variable of other files in C language, and the proper name must be used? (cannot add struct when using alias)

【324. 摆动排序 II】
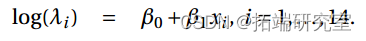
R language GLM generalized linear model: logistic regression, Poisson regression fitting mouse clinical trial data (dose and response) examples and self-test questions

数论 --- 欧拉函数、筛法求欧拉函数、欧拉定理、费马小定理详细证明
【Go语言刷题篇】Go从0到入门5:Map综合复习、条件语句、循环语句练习

5g NR MBS architecture introduction
随机推荐
1002_20181019
Configuration du mode tcwind
实型数运算
risc-v指令集
odoo15 Module operations are not possible at this time, please try again later or contact your syste
《数据安全法》出台一周年,看哪四大变化来袭?
Kettle (VI): full database backup based on kettle
数论 --- 欧拉函数、筛法求欧拉函数、欧拉定理、费马小定理详细证明
JVM memory structure
C#应用程序界面开发基础——窗体控制
Racher add / delete node
2280.Cupboards
jsp中获取session中的值
2022 P cylinder filling test exercises and online simulation test
jvm内存结构
压缩与解压缩命令
【学习笔记】因子分析
Pyinstaller打包pikepdf失败的问题排查
Design of secsha system
Pyinstaller打包pikepdf失败的问题排查