Optimized three-dimensional space positioning method and its fast implementation in C language

One 、 Three dimensional space positioning principle

Suppose we know the distance from ourselves to the positioning base station di （i=1 2 3 4…） And know the coordinates of the positioning base station , Then we can build in space n A circle centered on the coordinates of the base station , A space sphere with a distance of radius , The equation of the sphere is as follows . among a,b,c Is the base station coordinate ,r Is the absolute distance between the target and the base station .

Assume , We have three positioning base stations , So we can get a set of equations . The equations can be solved to two groups of real data . At this time, the height cannot be accurately determined , If you want to determine the exact height , We are about to introduce a base station , Form a system of equations with four equations . By solving this set of equations, we can get the coordinates we want .

But there is a problem here ： Using a single-chip microcomputer to solve a system of binary quadratic equations with three parameters is obviously not very important , Moreover, if there are too many people to be located or too many base stations, it will lead to coordinate update delay and other problems . So the author optimizes the calculation based on this problem .

Two 、 Fixed height

First, we detect the relative height of the target . Two base stations are set here A and B, Their coordinates are only Z The axis is different , That is, the two BTSs are as shown in the figure , At this time, the two spheres intersect with each other in the space , And the plane is parallel to the absolute plane （ ground ）. So we only need to consider the height of the plane

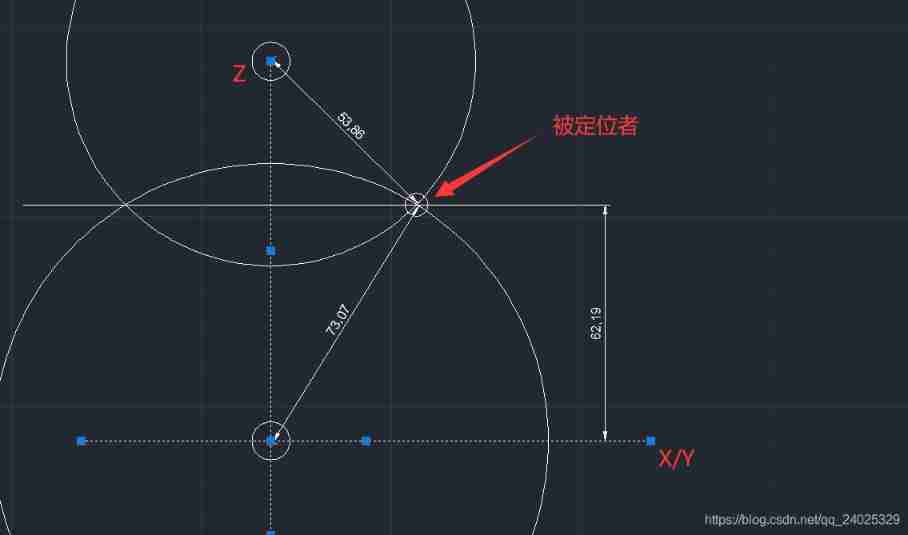
At this point, we get the simplified equations as

After simplification, it can be

Now the height is

3、 ... and 、 Space positioning to plane positioning

In the second section, we have used two base stations , And get the height of the target . Here we are setting up two base stations C and D, And guarantee that C and D And A or B In the same plane . Then we will locate the coordinates of the target , Use the height obtained in the second section to project to ACD The plane where it is , In this way, we can convert the space coordinates to the plane for calculation , I.e. not considering Z The problem with the axis . Here we list two equations

Simplify simultaneous equations , elimination XY The square term of the equation is obtained a

The physical meaning of the equation and the plane straight line obtained by the intersection of two circles in the plane . In the same way, simplification and amalgamation 1 3 Get the equation b

Summation equation a Sum equation b We can write it in the form of a matrix as follows

Here we make For matrix A. For matrix B. The coordinates obtained are

Four 、 verification

Here the author first uses CAD Draw a coordinate , Reuse MATLAB Calculate and verify .

clear
clc
A = [0 0];
B = [100 0];
C = [0 100];% Define coordinates 

La = 70;
Lb = 74.17;
Lc = 67.86;% Define the distance between the base station and the anchor point 

D = [2*A(1)-2*B(1) 2*A(2)-2*B(2);
     2*A(1)-2*C(1) 2*A(2)-2*C(2)]; % Define parameter matrix 
 
XY = [0;
      0];
  
Z = [(Lb^2 - La^2)+(A(1)^2 - B(1)^2)+(A(2)^2 - B(2)^2);
     (Lc^2 - La^2)+(A(1)^2 - C(1)^2)+(A(2)^2 - C(2)^2)];
 
XY = D^-1 * Z


%%=========== Running results ==============%%

XY =

   46.9941
   51.4751

5、 ... and 、 Use C Language implementation

use C Language implementation mainly needs to use C Language to do matrix inverse and matrix multiplication , The specific code is as follows

//================ Calculate the inverse of the matrix ================//
#include<stdio.h>
#define N 10
double Det(double arcs[N][N],int n)// Expand on the first line |A|
{
    double ans = 0;
    double temp[N][N];
    int i,j,k;
	double t;
    if(n==1)
    {
        return arcs[0][0];
    }
    for(i=0;i<n;i++)
    {
        for(j=0;j<n-1;j++)
        {
            for(k=0;k<n-1;k++)
            {
                temp[j][k] = arcs[j+1][(k>=i)?k+1:k];

            }
        }
        t = Det(temp,n-1);
        if(i%2==0)
        {
            ans += arcs[0][i]*t;
        }
        else
        {
            ans -=  arcs[0][i]*t;
        }
    }
    return ans;
}
void Minor(double arcs[N][N],double ans[N][N],int n)// Calculate the remainder of each element in each row and column , form A*
{
	int i,j,k,t;
    double temp[N][N];
    if(n==1)
    {
        ans[0][0] = 1;
        return;
    }
    for(i=0;i<n;i++)
    {
        for(j=0;j<n;j++)
        {
            for(k=0;k<n-1;k++)
            {
                for(t=0;t<n-1;t++)
                {
                    temp[k][t] = arcs[k>=i?k+1:k][t>=j?t+1:t];
                }
            }


            ans[j][i]  =  Det(temp,n-1);
            if((i+j)%2 == 1)
            {
                ans[j][i] = - ans[j][i];
            }
        }
    }
}
int main()
{
    double A[N][N] = {
   {-200,0},{0,-200}};
    double iA[N][N];  
    int i,j;
	double dA;
    dA = Det(A,2);
    Minor(A,iA,2);
    for(i=0;i<2;++i)
    {
        for(j=0;j<2;++j)
        {
            printf("%f ", A[i][j]);
        }
        printf("\n");
    }
    printf("\n");
    for(i=0;i<2;++i)
    {
        for(j=0;j<2;++j)
        {
            printf("%f ",(iA[i][j]/dA));
        }
        printf("\n");
    }
    return 0;
}

//======================= Matrix multiplication ===================//
#include "stdio.h"

void main()
{
	double Max1[2][2]={
   {7,8},{1,5}};
	double Max2[2][1]={
   {0.5},{0.3}};
	double Max3[2][1];
	unsigned char i,j;
	double ans=0;
	for(i=0;i<2;i++)
	{
		for(j=0;j<2;j++)
		{
			ans += Max1[i][j]*Max2[j][0];
		}
		Max3[i][0] = ans;
		ans = 0;
	}
	for(i=0;i<2;i++)
	{
		for(j=0;j<1;j++)
		{
			printf("%f ",Max3[i][j]);
		}
		printf("\n");
	}

}

6、 ... and 、 summary

This method is just an idea of the author and is not specifically used , We don't know how accurate this method is in case of actual error , To be tested by the author . The author's level is limited. Please correct any mistakes .