矩阵白化原理及推导

在看CSP算法时，发现用到了矩阵白化，所以在这里记录一下。
以下内容来自：【数学】矩阵白化原理及推导； 矩阵白化

矩阵白化目的

如对于任意一个矩阵$X$，对其求协方差，得到的协方差矩阵$cov(X)$并不一定是一个单位阵（对角阵）；【注意：协方差矩阵是对称矩阵，但不一定是对角阵】而矩阵白化就是找到一个变换矩阵$P$，使得$Y=PX$的协方差矩阵$cov(Y)$是一个单位阵（对角阵）。

因为通过矩阵白化后，协方差是个对角阵(单位阵)，那么就代表着矩阵$Y$的各个向量(向量是列向量还是行向量要根据求协方差时$cov(X)=X{X}^T$还是$X^{T}X$来判断)之间就不相关了。

或者说，矩阵白化的目的就是让被变换的矩阵经过变换后其向量的方差相同（因为是单位阵）。

矩阵白化推导

对于矩阵$X$，其协方差矩阵$cov(X)=X{X}^T$并不一定为对角矩阵，但是对于实对称的协方差矩阵可以有如下的特征值分解：

$$cov(X)=Q\Lambda Q^T$$

其中的$\Lambda$为由特征值组成的对角矩阵，$Q$为对应的特征向量，是一个正交矩阵。现在我们要找到线性变换矩阵$P$，使得$Y=PX$的协方差矩阵可以是单位阵，即

$$cov(Y)=Y{Y}^T=PX(PX{)}^T=PX{X}^T{P}^T=Pcov(X)P^T=E（单位阵）$$

现在令$P={\Lambda }^{-1/2}{Q}^T$（矩阵开根号就是其中的每个元素开根号），那么有

所以说当$P={\Lambda }^{-1/2}{Q}^T$时，可以使得$Y=PX$的协方差矩阵为单位阵(对角阵)。

因此 ，通过矩阵白化后，矩阵Y的各个向量(列向量还是行向量根据上文确定)之间就不相关了。

示意代码

clc, clear;

x = -10:.1:10;
x = x +randn(1,length(x));
y = 0.6*x + randn(1,length(x));
subplot(2,1,1)
plot(x, y, 'o')
axis ([-15 15 -10 10])

data = [x;y];
C = data*data';
[u,s,v] = svd(C);
W = diag(1./sqrt(diag(s)))*v';
b = W*data;
subplot(2,1,2)
plot(b(1,:),b(2,:),'o')
axis ([-15 15 -10 10])

可见白化其实就是让信号尽可能不相关。在分析PCA的时候，我们知道特征值与对应方向的方差有关联，所以白化就是这个思路：首先旋转坐标轴，其次根据对应方向的方差（特征值）进行伸缩，中心化的目的就是为了保证变换前后数据中心对应坐标轴中心，而不至于因为旋转/伸缩而偏离坐标原点太过分：

是不是觉得与PCA相像？后面给出分析。

秩亏缺矩阵的白化

当协方差矩阵为秩亏缺时，可以写为：

此时白化矩阵为：

$$P={D_{n\times n}}^{-1/2}{V}_1^H$$

白化后的信号：

$$Y=PX$$

此时白化后信号的协方差矩阵：

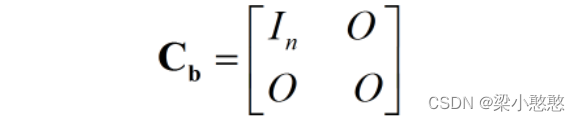
至此，完成白化。这也容易理解，有效信号占一个子空间，对子空间白化，就是对有效信号进行白化。

白化与PCA

PCA前文有分析，给出PCA步骤：

步骤一： 数据中心化——去均值；

步骤二： 求解协方差矩阵；

步骤三： 利用特征值分解/奇异值分解 求解特征值以及特征向量；

步骤四： 利用特征向量构造投影矩阵；

步骤五： 利用投影矩阵，得出降维的数据。

以上文二维数据为例：

• 中心化： 白化的中心化，PCA也需要中心化；
• 旋转： 白化步骤中的旋转，即旋转后的坐标就是PCA对应的第一、第二投影方向，如图中红线、绿线所示；
• 拉伸： 不同维度的特征值通常差别较大，在PCA中就是对特征值进行归一化。如果将不同维度的数据看作不同特征，白化步骤的拉伸本质也是特征的归一化。

参考文章

【数学】矩阵白化原理及推导

矩阵白化