leetcode 968. Monitoring binary tree

Title Description

Given a binary tree , We put cameras on the nodes of the tree .

Each camera head on a node can monitor its parent object 、 Itself and its immediate children .

Calculate the minimum number of cameras required for all nodes of the monitoring tree .
Example 1：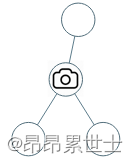

Input ：[0,0,null,0,0]
Output ：1
explain ： As shown in the figure , One camera is enough to monitor all nodes .
Example 2：

Input ：[0,0,null,0,null,0,null,null,0]
Output ：2
explain ： You need at least two cameras to monitor all the nodes in the tree . The image above shows one of the effective locations for the camera to be placed .

Tips ：

The range of the number of nodes in a given tree is [1, 1000].
The value of each node is 0.

analysis

This topic is an interesting tree DP+ Greedy problem , And the difficulty is not small , Many people find it difficult to understand the solution . If you've done it before A dance without a boss and Strategy game These two questions , You may think this question is very similar to the strategy game , The strategy game is to see all the edges , This question is to monitor all the points , The same is true , But this question is more difficult .

Let's try the conventional idea first ： Each node can choose whether to put the camera or not , If you have to put , Then place it ; Otherwise, take the minimum value of placing and not placing . in other words , For a node u Come on , If his parent node has not been covered by the camera , that u Node is to place a camera to monitor its parent node （ Here, consider whether it is really necessary to place ？）, If u The parent node of is overwritten to , Just try it separately u Which of the two options is better to place or not to place . The flaw in this idea lies in , We can't determine the node u Whether the camera must be placed , Because even if its parent node is not overwritten ,u No placement , stay u Can also be monitored by placing on the sibling nodes of u Parent node ; But if we all want to let brother nodes play , As a result, both children didn't put a camera , The plan is illegal , So this kind of thinking doesn't work .

Think about linear DP problem , The state of a position , Or it can be transferred from its left position , Or it can be transferred from the right state , however The transition direction of the state must be unidirectional , This is a DP The state of having no aftereffect requirements . for instance f[2] from f[1] Roll out in turn affects f[1], This is clearly unreasonable . The reason to say this , It's because of the shape of the tree DP We can only do one-way state transition , Or only consider the state of the parent node , Or only consider the state of the child node , In this way, there can be a reasonable state transition sequence . The above idea is to consider only the state of the parent node to transfer , It turns out that it depends on the state of the sibling nodes , So it's not possible . Since it doesn't work from top to bottom , Try bottom-up . If you don't think of the irrationality of pushing the state from top to bottom , I don't understand why many people say that this problem should be calculated from the bottom up .

Get to the point . For the node u, We only deduce its state according to the state of its child node . There are three types of node states ：

• 0 Means not covered by , That is, there is no camera in this position , The child node is not equipped with a camera
• 1 Means to be covered by , Explain that the child node has a camera , But it doesn't have a camera
• 2 Indicates that a camera is placed at this position , Nature is also covered

For the node u for ：

If there is any child node that has not been overwritten （ Status as 0）, that u A camera must be placed on the to ensure that the child is monitored , here u The state of is 2.（ This is the difference between the top-down and bottom-up solutions , A node may have two children , But there is only one parent node , The parent node has no choice , Only cameras can be placed ）.

If the status of its child nodes is 1, That is, it is covered by , Now? u It doesn't matter whether the child lives or dies , Just think about whether you can let it go , Choose not to place here . ** This is out of greed , because u Your child's status is 1, It means that there is no camera , The child node cannot monitor u, If in u Node placement camera , The monitoring range that can be increased is u and u Parent node ; If not u Place at , stay u Place the camera at the parent node of , The monitoring scope that may be increased is u and u Brother node of ,u The parent node of and u The grandfather node of ; Since they all add a camera , We naturally choose a wider range of options that can be increased , Such a scheme would be optimal . ** This situation u Do not place the camera , Nor can it be monitored by child nodes , State is 0. Of course, do not worry that this node will not be monitored , Because as long as u There are parent nodes , The child node cannot be monitored , There must be a camera .

If there are cameras installed in the child nodes , That is to say, the state is 2 The node of ,u The nodes are covered by , Naturally, there is no need to place a camera , It is also a greedy thought , here u The state of is 1, No camera is placed but can be covered .

u Up to two children , The state of their children is nothing more than the existence of at least one 0, All are 1, There is at least one 2 One of the three , The state division is not repeated . There is also a boundary problem to consider , That is, the state of the empty node ,NULL The node state of the is naturally not 2, Because it cannot monitor its parent node ; It's not a state 0, Because it does not need to be monitored by its parent node ; So its state is zero 1, It can be monitored but no camera is installed , This will not affect the leaf node and the degree is 1 The node state of .

The last two questions . How to conduct state transition from bottom to top ？ The order of state transition is from the left and right subtrees to the root node , So the state transition can be carried out in the order of subsequent traversal . The second question is , We can define one dfs Function to find dfs（u）, That is to say, return to u After the state transition for the subtree of the root u The state of , If in the end u The state of is 0 What to do with ？ We move from bottom to top , Each state is only responsible for the child node , Not responsible for the parent node , So if the last root node is not overwritten , Add a camera .
One of the subtleties of this code is dfs Only return u The final state of , During traversal, if the status is 2 The number of nodes is increased , So the final count is the number of cameras .
The code of this topic is very simple , The analysis process is complex , If you can feel the subtlety of the analysis process , Believe in the tree DP The understanding of is very rewarding .

Code

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int res = 0;
    int dfs(TreeNode* root) {
        if(!root)   return 1;// Can be covered by 
        int l = dfs(root->left);
        int r = dfs(root->right);
        if(l == 0 || r == 0) {
            res++;
            return 2;// Place the camera 
        }
        if(l == 2 || r == 2)    return 1;// Can be covered by 
        return 0;// Cannot be overwritten ,l = r = 1
    }
    int minCameraCover(TreeNode* root) {
        if(!dfs(root))   res++;
        return res;
    }
};