概率论的学习整理1： 集合和事件

写在最前面的话

• 整理数学，是工作涉及到了，也是编程需要用到
• 所以我重新学了一段时间了，多年未学习了，几乎是从头开始了，不自己写，感谢学了也会忘记，另外本地文档确实很没用，还是写网上文档把
• CSDN的各种评价体系，我不care，我只是记个学习笔记
• 尽量写的让初学者也能看懂，那就更好了。

关于我学习概率论的几个事情

• 我觉得学概率，肯定不能是为了做题，也不能靠做题
• 如果问是问了什么？是为了解决问题，另外，希望孩子学概率论的时候能给孩子讲明白
• 学习的小目标呢？

1.  弄清楚原理
2. 理清楚知识体系，用脑图整理下。我觉得不能遇到概率提就想起各种公式，套公式，而是应该有个思路，能用树状图或者2维表展开，展开思考才行，后面的都应该是顺水推舟的事情。
3. 整理一下不同的解题思路，以后遇到类似问题提高效率

1 集合 set

1.1 集合的基础概念

 

 1.2 韦恩图，文氏图

1.3 韦恩图很有用

比如全概率公式

• P(B)=P(A) *P(B|A) + P(A')*P(B|A') 
• 很多人觉得并不好理解
• 用下面这个图来理解全概率公式呢，很简单

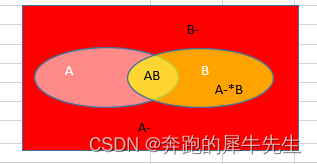
• RGB原理，红色和黄色，合成橙色！
• 可以看到B集合是AB 和 A-*B这两部分组合成的！这两个部分又刚好是2个交集！展开即可得到全概率公式！
• P(B)=P(AB) + P(BA') 
• P(B)=P(A∩B) + P(B∩A') 
• P(B)=P(B|A) *P(A)+ P(B|A') *P(A')

1.4 基本的集合关系

• 和事件
• P(AUB)= P(A) + P(B)  -P(A∩B) 

2  实验和事件

2.1 先贴下本地的笔记图

 

 

 

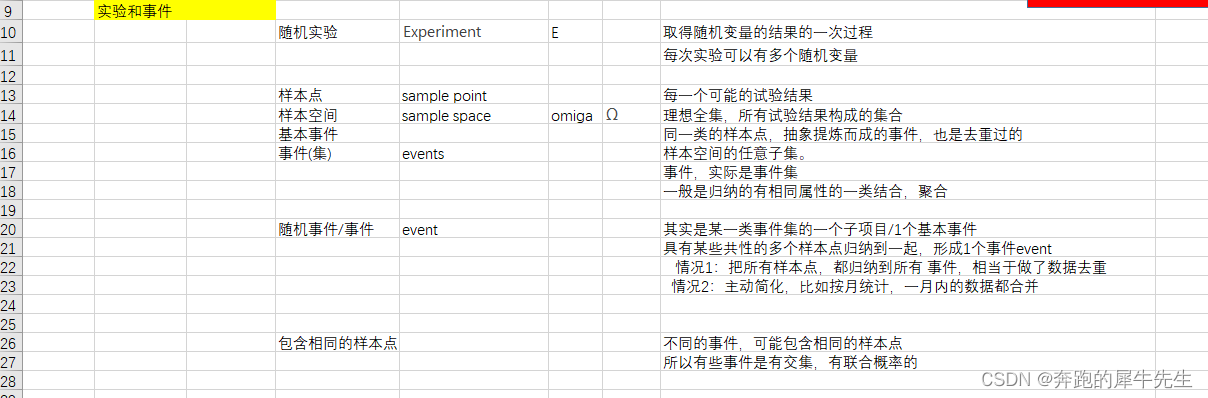
2.2  重要概念

2.2.1 事件  event

• 事件是对 样本点的提炼
• 基本事件是去重的
• 事件是通过不同视角，对所有样本点进行的归类，聚合，提炼

1. 比如有时候可以按月统计，有时候按日统计
2. 可以统计次数，可以只管某一次等等

• 一个实验里可以定义出很多不同的事件

1. 比如做10次硬币实验，求最后一次为正面的概率
2. 做10次硬币实验，求出现正面的概率
3. 做10次硬币实验，求出现正面3次的概率
4. 做10次硬币实验，求出现正面3次背面2次的概率
5. 。。。
6. 求1年中每天下雨的概率
7. 求1年中每个月下雨的天数期望

2.2.2   事件集  events

• 因为样本空间的子集有很多很多
• 事件集是一类有相同特点的事件的集合
• 比如10次硬币实现，出现3次证明的事件集，可以拆解成，第1次出现证明，第2次出现正面，等等。。。。

2.2.3   互斥事件

• 简单的说，就是，互斥事件A和B，永远不会同时发生
• A和B，同时发生的概率为0
• A和B，两个集合，永远没用交集部分！
• P(A∩B)=0
• 联合概率为0,  P(AB)=0
• 条件概率为0，P(A|B)=P(B|A)=0
• A和B互斥，一定不独立

2.2.4 对立事件

• 对立就是，有你没我
• 整个样本空间，样本划分只有这2个事件，那这2个事件就是独立事件，否则不是
• 比如可以划分为3个事件，那这3个事件就不对立

2.2.5 独立事件

• 相互独立，并不意味着交集为0
• 而意味着，两个集合A和B的交集，可以直接转为两者本身相乘
• 这个是否是可以从坐标系投影来思考？
• 独立一定不互斥，而是相容的，投影交叉的？

• P(AB)= P(A)P(B）联合概率等于两者相乘，可以同时发生，同时发生概率=两者自身概率乘积，不互相影响
• P(A | B)=P(A)
• P(B | A)=P(B)
• P(AB)=P(A∩B)=P(A)P(B | A) = P(A)P(B）
• P(AB)=P(A∩B)=P(B)P(A | B) = P(A)P(B）
• P(AB) = P(A)P(B）