Using rank to discuss the solution of linear equations / the positional relationship of three planes

Discuss the positional relationship of three planes with rank / Solutions of linear equations

System of linear equations
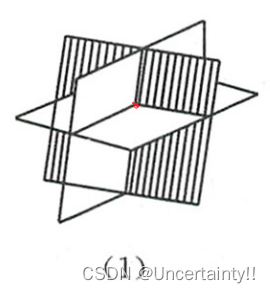
The three equations in the figure below correspond to three planes

Augmented matrix form of linear equations

Whether the equations have solutions , Manifested as Whether the three planes have a common intersection , There are several solutions in Three planes have several common intersections

Situation 1 ：$r(\bar{A})=r(A)=3$【 Number of equations 3 $=$ The number of unknowns 3】, The system of equations has a unique solution , Three planes intersect at a point

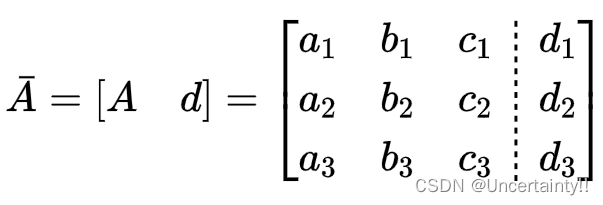
Situation two ：$r(\bar{A})=3$,$r(A)=2$,$r(\bar{A})\ge r(A)$, The equations have no solution 【 because $0z_3=d_3$ unsolvable 】, Three planes have no common intersection , Because of $r(A)=2$ Then there must be two planes intersecting

Augmented matrix No 3 The line may be the same as 1 Yes or no 2 Row proportional , Maybe not 0, Write here as 0 Just to show the rank clearly

There are two cases when three planes have no common intersection
1. Three planes intersect in pairs , But there is no common intersection , Therefore, the equations have no solution

2. Two of the three planes intersect , The other plane is parallel to one of them , But there is no common intersection , Therefore, the equations have no solution

Situation three ：$r(\bar{A})=r(A)=2<n=3$（ Number of equations 2 $<$ The number of unknowns n=3 ）, The equations have infinite solutions 【 because $0z_3=0$】, Three planes have infinite common intersections , Because of $r(A)=2$ Then there must be two planes intersecting , Because of $r(\bar{A})=2$ It shows that at least two of the three planes are different from each other

Augmented matrix No 3 The line may be the same as 1 Yes or no 2 Row proportional , Maybe not 0, Write here as 0 Just to show the rank clearly

There are two cases when two planes have no common intersection
1. Two planes intersect , The other plane passes through the intersection , The three planes are different from each other , Because the three planes meet in a line , There are countless points on the intersection , Therefore, in this case, the equations have infinite solutions

2. Two planes intersect , The other plane coincides with one of them , The two planes are different from each other , Because three planes （ The two planes coincide ） On the front line , There are countless points on the intersection , Therefore, in this case, the equations have infinite solutions

Situation four ：$r(\bar{A})=2$,$r(A)=1$,$r(\bar{A})<r(A)$, The equations have no solution 【 because $0z_2=d_2$ unsolvable 】, The three planes do not intersect , Because of $r(A)=1$, So no two planes intersect , So the three planes are parallel , Reanalysis $r(\bar{A})=2$, Therefore, at least two planes of three planes are different from each other

Augmented matrix No 2、3 The line may be the same as 1 Row proportional , Maybe not 0, Write here as 0 Just to show the rank clearly

At least two planes of three planes are different from each other in two cases
1. The three planes are parallel , And the three planes are different from each other , Three planes have no common intersection , Therefore, the equations have no solution

2. The three planes are parallel , Two planes coincide , At the same time, two planes are different from each other , Three planes （ The two planes coincide ） No common intersection , Therefore, the equations have no solution

Situation five ：$r(\bar{A})=r(A)=1<n=3$, The equations have infinite solutions , Three planes have infinite common intersections . from $r(A)=1$ know , No two planes intersect . and $r(\bar{A})=1$ It shows that at least one of the three planes is different from each other , There are two situations ,2 Planes are exclusive or 3 The two planes are different from each other , Both of these cases contradict the fact that there are infinite intersections in the three planes , Therefore, the three planes coincide

Augmented matrix No 2、3 The line may be the same as 1 Row proportional , Maybe not 0, Write here as 0 Just to show the rank clearly