当前位置:网站首页>Xctf attack and defense world crypto advanced area best_ rsa
Xctf attack and defense world crypto advanced area best_ rsa
2022-07-03 19:26:00 【l8947943】
1. Enter the environment , Download the attachment
Compressed package for topic , Include 4 File , Pictured :
given 2 Public key files and 2 Ciphertext file , With regular RSA Decryption methods: decrypt separately , Decryption failed (n by 2048 Bits are hard to decompose )
2. Problem analysis
- Continue to review RSA
- In plain text m, The secret is c, modulus n = p * q
- Use Euler functions ,φ(n) = (p - 1) * (q- 1)
- Select a large integer e, bring gcd(e, φ(n) ) = 1,e Used to encrypt the secret key
- Private key d It can be calculated from the value of Euler function , Satisfy ed mod φ(n) ≡ 1
- In plain text m Encrypted into ciphertext c:m^e ≡ c (mod n)
- Will ciphertext c Decrypt to plaintext m:c^d ≡ m (mod n)
- Common mode attack
Guess it should be the same plaintext , Used 2 Different public key encryption results in different ciphertexts , Using the same modulus and different public key indices for multiple encryption of the same plaintext may lead to common mode attacks .
Look at the boss's wp after :https://blog.csdn.net/weixin_44795952/article/details/108933406, Understand what common mode attack is
So called common mode , Is plaintext m identical , model n identical , Use two public keys e1,e2 Encrypt to get two private keys d1,d2 And two ciphertexts c1,c2
Common mode attack , When n Without change , know n,e1,e2,c1,c2 . Can be in the don't know d1,d2 Under the circumstances , figure out m.
There's a condition , namely
gcd(e1,e2)=1
- Attack principle
There are integers s 1 s_{1} s1, s 1 s_{1} s1( One is one minus one. ), Satisfy :
e 1 ∗ s 1 + e 2 ∗ s 2 = 1 e_{1} * s_{1} + e_{2} * s_{2} = 1 e1∗s1+e2∗s2=1
from Crypto.Util.number import long_to_bytes, bytes_to_long
from Crypto.PublicKey import RSA
from gmpy2 import gcd, invert
def egcd(a, b):
if a == 0:
return b, 0, 1
else:
g, y, x = egcd(b % a, a)
return g, x - (b // a) * y, y
with open('pic/publickey1.pem', 'rb') as f:
f1 = f.read()
pub1 = RSA.importKey(f1)
n = int(pub1.n)
e1 = int(pub1.e)
with open('pic/publickey2.pem', 'rb') as f:
f2 = f.read()
pub2 = RSA.importKey(f2)
e2 = int(pub2.e)
with open('pic/cipher1.txt', 'rb') as f:
c1 = f.read()
c1 = bytes_to_long(c1)
print(c1)
with open('pic/cipher2.txt', 'rb') as f:
c2 = f.read()
c2 = bytes_to_long(c2)
print(c2)
print(gcd(e1, e2))
s = egcd(e1, e2)
s1 = s[1]
s2 = s[2]
if s1 < 0:
s1 = -s1
c1 = invert(c1, n)
elif s2 < 0:
s2 = -s2
c2 = invert(c2, n)
m = pow(c1, s1, n) * pow(c2, s2, n) % n
print(m)
print(long_to_bytes(m).decode())
边栏推荐
- Why should we do feature normalization / standardization?
- 2022.2.14 Li Kou - daily question - single element in an ordered array
- Chapter 2: find the box array, complete number in the specified interval, and improve the complete number in the specified interval
- Simple solution of physical backup and restore of Damon database
- SQL injection for Web Security (1)
- We have built an intelligent retail settlement platform
- [new year job hopping season] test the technical summary of interviewers' favorite questions (with video tutorials and interview questions)
- 我們做了一個智能零售結算平臺
- Chapter 1: sum of three factorials, graph point scanning
- Php based campus lost and found platform (automatic matching push)
猜你喜欢

Flume learning notes
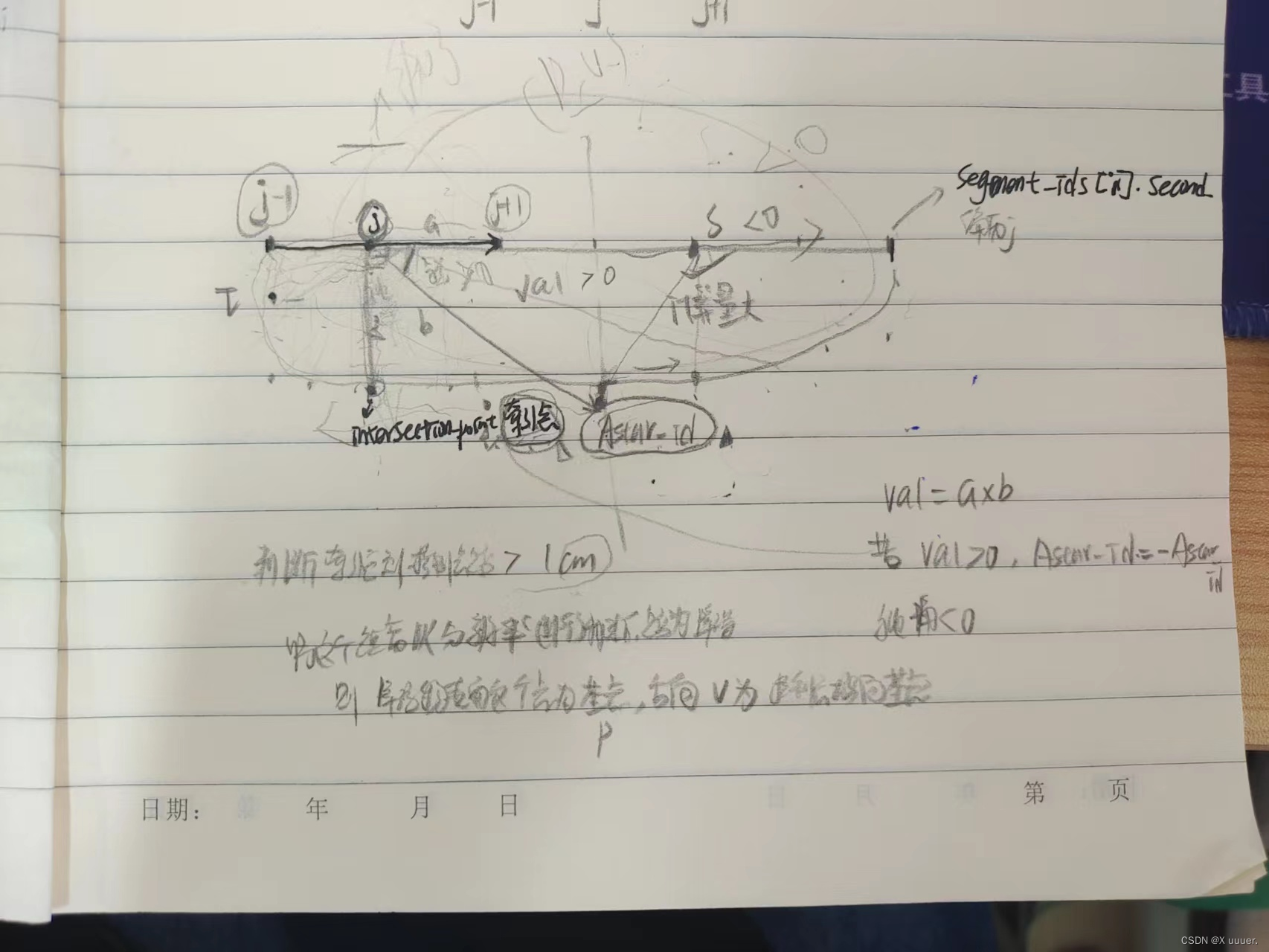
Ego planner code parsing Bspline_ Optimizer section (2)

Day18 - basis of interface testing

Basic principle of LSM tree
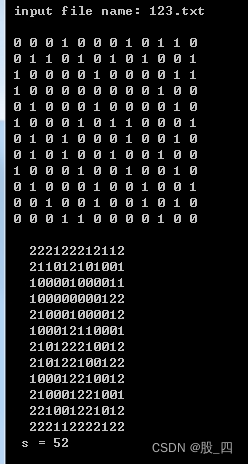
第一章:求所有阶乘和数,大奖赛现场统分程序设计,三位阶乘和数,图形点扫描,递归求n的阶乘n!,求n的阶乘n!,舍罕王失算
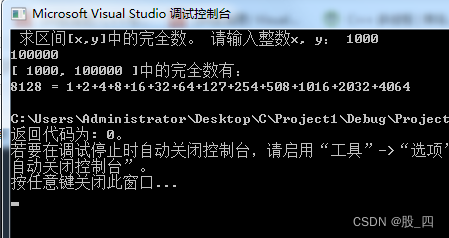
第二章:求长方体数组,指定区间内的完全数,改进指定区间内的完全数
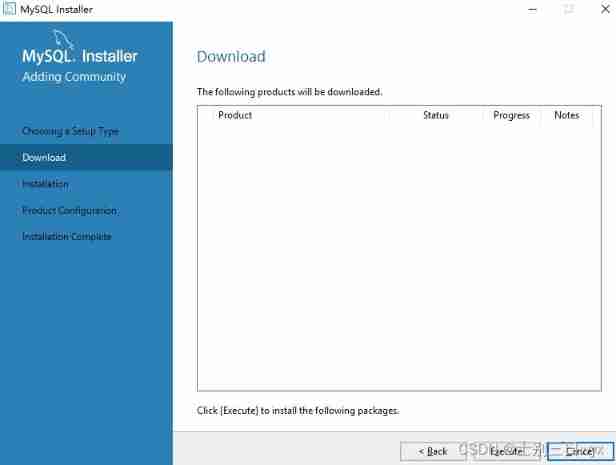
During MySQL installation, the download interface is empty, and the components to be downloaded are not displayed. MySQL installer 8.0.28.0 download interface is empty solution

2020 intermediate financial management (escort class)

02 -- QT OpenGL drawing triangle

【疾病识别】基于matlab GUI机器视觉肺癌检测系统【含Matlab源码 1922期】
随机推荐
Simulation scheduling problem of SystemVerilog (1)
Webrtc[41] - Analysis of the establishment process of webrtc transmission channel
Read the paper glodyne global topology preserving dynamic network embedding
Free hand account sharing in September - [cream Nebula]
PR 2021 quick start tutorial, how to create new projects and basic settings of preferences?
Chapter 1: find all factorial sums, Grand Prix site unified programming, three factorial sums, graphic point scanning, recursive factorial n of n!, Find the factorial n of n!, King Shehan miscalculate
Recommend a GIF processing artifact less than 300K - gifsicle (free download)
Chapter 1: seek common? Decimal and S (D, n)
Valentine's Day - make an exclusive digital collection for your lover
Chapter 1: drinking soft drinks, step tariff calculation, step tariff calculation function, personal income tax, solving square root inequality, simplifying solving square root inequality, solving dem
Why should the gradient be manually cleared before back propagation in pytorch?
Difference between surface go1 and surface GO2 (non professional comparison)
SQL injection for Web Security (1)
The earliest record
[wallpaper] (commercially available) 70 wallpaper HD free
Day18 - basis of interface testing
math_泰勒公式
Merge K ascending linked lists
During MySQL installation, the download interface is empty, and the components to be downloaded are not displayed. MySQL installer 8.0.28.0 download interface is empty solution
Summary of 90 day learning materials and notes of Zhang Fei's actual electronic hardware engineer