236. 二叉树的最近公共祖先

打卡!!!每日一题

今天给大家带来一道树类型的题目，也是一道比较经典的深度优先遍历的题目

题目描述：236. 二叉树的最近公共祖先

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

题目示例：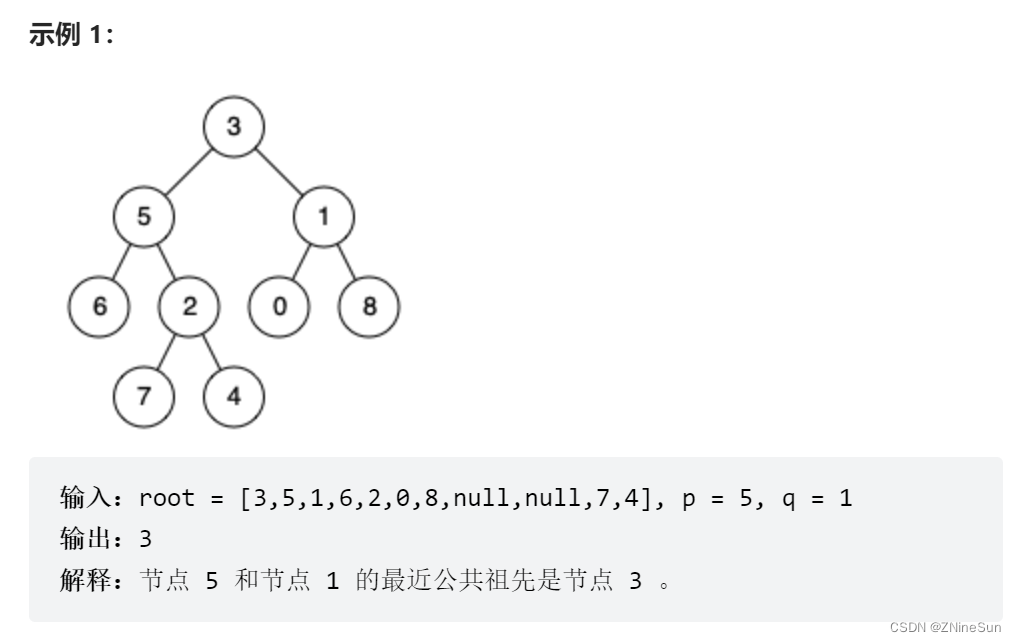

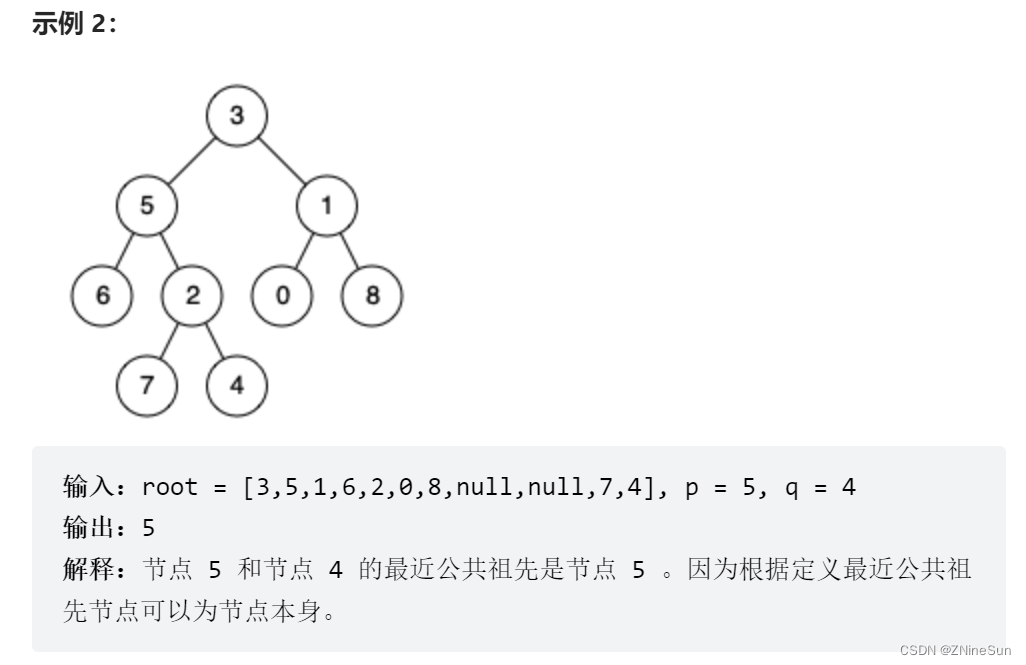
题目大概可以分为以下几种情形：

• 如果两个节点中有任意一个是根节点，那么我们就可以直接返回根节点
• 如果两个节点在树的两侧，那么他们最近的公共祖先也只能是根节点
• 最难的情况便是两个节点在树的同一侧

对于p或q是根节点的情况，我们只需判断p或q是否和根节点相等即可

if (p.val == root.val || q.val == root.val) {
    
            return root;
        }

判断是否在树的两侧，我们只需划分左右子树即可

        int rootIndex = allNodeVal.indexOf(root.val);
        int pIndex = allNodeVal.indexOf(p.val);
        int qIndex = allNodeVal.indexOf(q.val);
        /**2.两个节点在树的两侧**/
        if (pIndex < rootIndex && qIndex > rootIndex || pIndex > rootIndex && qIndex < rootIndex) {
    
            return root;
        }

两个节点在同一侧的话，我们需要用一个Hash表存储每个节点的所有父节点，然后获取p,q的父节点列表，因为我们需要层数最深的父节点 ，所以我们可以考虑采用中序遍历二叉树，这样的话层数最深的结点就会在链表的前面

    public void dfs(TreeNode root) {
    
        if (root == null) return;
        if (root.left != null) {
    
            parent.put(root.left.val, root);
            dfs(root.left);
        }
        if (root.right != null) {
    
            parent.put(root.right.val, root);
            dfs(root.right);
        }
    }

完整代码如下：

package com.exercise.leetecode.problem.剑指offer.前中后序遍历;

import com.exercise.leetecode.common.TreeNode;

import java.util.*;

public class 二叉树的最近公共祖先_236 {
    
    Map<Integer, TreeNode> parent = new HashMap<Integer, TreeNode>();
    List<Integer> allNodeVal = new ArrayList<>();
    TreeNode r;//存放根节点

    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
    
        /**1.说明其中有一个结点是根节点**/
        if (p.val == root.val || q.val == root.val) {
    
            return root;
        }
        //判断两个节点是否在同一侧
        r = root;
        dfs_in(root);
        root = r;
        boolean sig_p = false, sig_q = false;
        int rootIndex = allNodeVal.indexOf(root.val);
        int pIndex = allNodeVal.indexOf(p.val);
        int qIndex = allNodeVal.indexOf(q.val);
        /**2.两个节点在树的两侧**/
        if (pIndex < rootIndex && qIndex > rootIndex || pIndex > rootIndex && qIndex < rootIndex) {
    
            return root;
        }
        dfs(root);
        List<TreeNode> pParent = new ArrayList<>();
        pParent.add(p);
        while (p != null) {
    
            p = parent.get(p.val);
            pParent.add(p);
        }
        List<Integer> qParent = new ArrayList<>();
        qParent.add(q.val);
        while (q != null) {
    
            q = parent.get(q.val);
            if (q != null) {
    
                qParent.add(q.val);
            }

        }
        for (TreeNode t : pParent) {
    
            if (qParent.contains(t.val)) {
    
                return t;
            }
        }
        return null;
    }

    public void dfs_in(TreeNode root) {
    
        if (root == null) {
    
            return;
        }
        dfs_in(root.left);
        allNodeVal.add(root.val);
        dfs_in(root.right);
    }

    public void dfs(TreeNode root) {
    
        if (root == null) return;
        if (root.left != null) {
    
            parent.put(root.left.val, root);
            dfs(root.left);
        }
        if (root.right != null) {
    
            parent.put(root.right.val, root);
            dfs(root.right);
        }
    }
}