[set theory] relational power operation (relational power operation | examples of relational power operation | properties of relational power operation)

One 、 Relational power operation

---

Relationship

R

R

R Of

n

n

n Power definition :

R

⊆

A

×

A

,

n

∈

N

R \subseteq A \times A , n \in N

R⊆A×A,n∈N

{

R

0

=

I

A

R

n

+

1

=

R

n

∘

R

(

n

≥

0

)

\begin{cases} R^0 = I_A & \\ R^{n +1} = R^n \circ R & ( n \geq 0 ) \end{cases}

{ R0=IA​Rn+1=Rn∘R​(n≥0)​

Relationship

R

R

R yes aggregate

A

A

A Upper Binary relationship ,

R

R

R Of

0

0

0 The next power

R

0

R^0

R0 It's an identity relationship

I

A

I_A

IA​ , Relationship

R

R

R Of

n

+

1

n + 1

n+1 The power is equal to

R

n

+

1

=

R

n

∘

R

R^{n + 1} = R^n \circ R

Rn+1=Rn∘R among

n

≥

0

n \geq 0

n≥0 ;

R

1

=

R

0

∘

R

=

R

R^1 = R^0 \circ R = R

R1=R0∘R=R , Identity relation and Relationship

R

R

R Reverse order synthesis , The result is still related

R

R

R , This relationship

R

R

R It can be any relationship ;

The identity relationship is aggregate

A

A

A Each element in has its own relationship with itself ;

Relationship

R

R

R Power operation result

R

n

R^n

Rn Relationship It's also a collection

A

A

A The binary relationship on , So there is

R

n

⊆

A

×

A

R^n \subseteq A \times A

Rn⊆A×A

Relationship

R

R

R Of

n

n

n The next power , Namely

n

n

n individual

R

R

R Relationship reverse order synthesis :

R

n

=

R

∘

R

∘

⋯

∘

R

⏟

n

individual

R

The inverse

order

close

become

R^n = \begin{matrix} \underbrace{ R \circ R \circ \cdots \circ R } \\ n individual R Reverse order synthesis \end{matrix}

Rn=


R∘R∘⋯∘R​n individual R The inverse order close become ​

Two 、 Examples of relational power operations

---

aggregate

A

=

{

a

,

b

,

c

}

A = \{ a, b, c \}

A={ a,b,c} Relationship

R

R

R yes aggregate

A

A

A The binary relationship on ,

R

⊆

A

×

A

R \subseteq A \times A

R⊆A×A ,

R

=

{

<

a

,

b

>

,

<

b

,

a

>

,

<

a

,

c

>

}

R = \{ <a,b> , <b,a> , <a, c> \}

R={ <a,b>,<b,a>,<a,c>}

Relationship

R

R

R Of Number of power sets :

A

A

A It's a finite set ,

A

A

A The number of ordered pairs on is

3

×

3

=

9

3 \times 3 = 9

3×3=9 individual ,

A

A

A The number of binary relations on , That is, the number of power sets of ordered pairs , yes

2

3

×

3

=

512

2^{3\times 3} =512

23×3=512 individual ;

Relationship

R

R

R Of

0

0

0 The next power :

R

0

=

I

A

R^0 = I_A

R0=IA​ ,

R

R

R Relational

0

0

0 Power is an identity relationship , Graph is that every vertex has a ring , There is no relationship between vertices ;

Relationship

R

R

R Of

1

1

1 The next power :

R

1

=

R

0

∘

R

=

R

R^1 = R^0 \circ R = R

R1=R0∘R=R , Identity

I

A

I_A

IA​ With any relationship in reverse order , The result is still that relationship ;

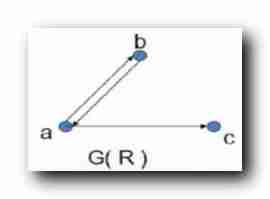
Relationship

R

R

R Of

2

2

2 The next power :

R

2

=

R

0

∘

R

=

R

∘

R

=

{

<

a

,

b

>

,

<

b

,

a

>

,

<

a

,

c

>

}

∘

{

<

a

,

b

>

,

<

b

,

a

>

,

<

a

,

c

>

}

=

{

<

a

,

a

>

,

<

b

,

b

>

,

<

b

,

c

>

}

\begin{array}{lcl}R^2 & = & R^0 \circ R \\\\ &=& R \circ R \\\\ &=& \{ <a,b> , <b,a> , <a, c> \} \circ \{ <a,b> , <b,a> , <a, c> \} \\\\ &=& \{ <a,a>, <b, b> , <b,c> \}\end{array}

R2​====​R0∘RR∘R{ <a,b>,<b,a>,<a,c>}∘{ <a,b>,<b,a>,<a,c>}{ <a,a>,<b,b>,<b,c>}​

Note that the above

∘

\circ

∘ Reverse order synthesis during operation , Synthesize the previous relationship from the latter relationship ;

Relationship

R

R

R Of

3

3

3 The next power : And

R

1

R_1

R1​ identical

R

3

=

R

1

∘

R

=

{

<

a

,

a

>

,

<

b

,

b

>

,

<

b

,

c

>

}

∘

{

<

a

,

b

>

,

<

b

,

a

>

,

<

a

,

c

>

}

=

{

<

a

,

b

>

,

<

a

,

c

>

,

<

b

,

a

>

}

=

R

1

\begin{array}{lcl}R^3 & = & R^1 \circ R \\\\ &=& \{ <a,a>, <b, b> , <b,c> \} \circ \{ <a,b> , <b,a> , <a, c> \} \\\\ &=& \{ <a,b>, <a, c> , <b,a> \} \\\\ &=& R^1 \end{array}

R3​====​R1∘R{ <a,a>,<b,b>,<b,c>}∘{ <a,b>,<b,a>,<a,c>}{ <a,b>,<a,c>,<b,a>}R1​

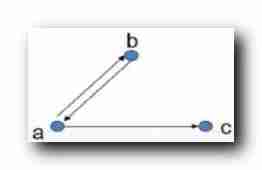
Relationship

R

R

R Of

4

4

4 The next power : And

R

2

R_2

R2​ identical

Relationship

R

R

R Of

5

5

5 The next power : And

R

1

R_1

R1​ identical

Relationship

R

R

R Of

2

k

2k

2k Even power (

k

=

1

,

2

,

⋯

k=1,2, \cdots

k=1,2,⋯ ) : And

R

2

R_2

R2​ identical

Relationship

R

R

R Of

2

k

+

1

2k + 1

2k+1 Odd power (

k

=

0

,

1

,

2

,

⋯

k=0,1,2, \cdots

k=0,1,2,⋯ ) : And

R

1

R_1

R1​ identical

3、 ... and 、 Properties of relational power operation

---

Properties of relational power operation :

Relationship

R

R

R yes aggregate

A

A

A Relationship on ,

R

⊆

A

×

A

R \subseteq A \times A

R⊆A×A ,

m

,

n

m,n

m,n It's a natural number ,

m

,

n

∈

N

m,n \in N

m,n∈N ; Relational power operation has the following two properties :

R

m

∘

R

n

=

R

m

+

n

R^m \circ R^n = R^{m + n}

Rm∘Rn=Rm+n

(

R

m

)

n

=

R

m

n

(R^m ) ^n = R^{m n}

(Rm)n=Rmn