[set theory] relationship properties (symmetry | symmetry examples | symmetry related theorems | antisymmetry | antisymmetry examples | antisymmetry theorems)

One 、 symmetry

---

symmetry describe :

R

⊆

A

×

A

R \subseteq A \times A

R⊆A×A

R

R

R It's symmetrical

⇔

\Leftrightarrow

⇔

∀

x

∀

y

(

x

∈

A

∧

y

∈

A

∧

x

R

y

→

y

R

x

)

\forall x \forall y ( x \in A \land y \in A \land xRy \to yRx )

∀x∀y(x∈A∧y∈A∧xRy→yRx)

⇔

\Leftrightarrow

⇔

(

∀

x

∈

A

)

(

∀

y

∈

A

)

[

x

R

y

→

y

R

x

]

( \forall x \in A ) (\forall y \in A)[xRy \to yRx]

(∀x∈A)(∀y∈A)[xRy→yRx]

R

R

R It's asymmetric

⇔

\Leftrightarrow

⇔

∃

x

∃

y

(

x

∈

A

∧

y

∈

A

∧

x

R

y

∧

¬

y

R

x

)

\exist x \exist y ( x \in A \land y \in A \land xRy \land \lnot yRx )

∃x∃y(x∈A∧y∈A∧xRy∧¬yRx)

Symmetry description : Choose any two elements

x

,

y

x, y

x,y , If

x

x

x And

y

y

y It matters

R

R

R namely

x

R

y

xRy

xRy , that

y

y

y And

x

x

x It also matters

R

R

R namely

y

R

x

yRx

yRx ;

Asymmetric description : As long as there is one

x

,

y

x , y

x,y Combine ,

x

x

x And

y

y

y It matters

R

R

R , however

y

y

y And

x

x

x It doesn't matter.

R

R

R , Then the relationship

R

R

R It's asymmetric ;

Two 、 Example of symmetry

---

Example of symmetry :

In the diagram , Do not consider the ring , Just look at the relationship between the two points , The relationship between the two vertices is a round-trip arrow , So it's symmetrical , There is a one-way arrow , It's not symmetrical ;

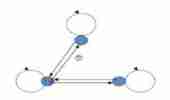
In the above diagram , Arrows between vertices are bidirectional , The relationship is symmetric ;

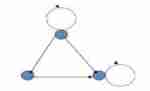
In the above diagram , They are all one-way arrows , One arrow is unidirectional , It's not symmetrical ;

3、 ... and 、 Symmetry theorem

---

Symmetry theorem :

R

R

R It's symmetrical

⇔

\Leftrightarrow

⇔

R

−

1

=

R

R^{-1} = R

R−1=R

⇔

\Leftrightarrow

⇔

R

−

1

R^{-1}

R−1 It's symmetrical

⇔

\Leftrightarrow

⇔

M

(

R

)

M(R)

M(R) The relation matrix is symmetric

⇔

\Leftrightarrow

⇔

G

(

R

)

G(R)

G(R) If there is an edge between any two vertices of , It must be two sides ( One in the forward direction and one in the reverse direction )

symmetry Between two vertices Yes

0

0

0 Or

2

2

2 side ;

Four 、 Antisymmetry

---

Antisymmetry :

R

⊆

A

×

A

R \subseteq A \times A

R⊆A×A

R

R

R It's antisymmetric

⇔

\Leftrightarrow

⇔

∀

x

∀

y

(

x

∈

A

∧

y

∈

A

∧

x

R

y

∧

y

R

x

→

x

=

y

)

\forall x \forall y ( x \in A \land y \in A \land xRy \land yRx \to x=y )

∀x∀y(x∈A∧y∈A∧xRy∧yRx→x=y)

⇔

\Leftrightarrow

⇔

(

∀

x

∈

A

)

(

∀

y

∈

A

)

[

x

R

y

∧

y

R

x

→

x

=

y

]

(\forall x \in A)(\forall y \in A)[ xRy \land yRx \to x = y ]

(∀x∈A)(∀y∈A)[xRy∧yRx→x=y]

Non antisymmetry :

R

R

R Yes no antisymmetric

⇔

\Leftrightarrow

⇔

∃

x

∃

y

(

x

∈

A

∧

y

∈

A

∧

x

R

y

∧

y

R

x

∧

x

≠

y

)

\exist x \exist y ( x \in A \land y \in A \land xRy \land yRx \land x \not=y )

∃x∃y(x∈A∧y∈A∧xRy∧yRx∧x​=y)

Antisymmetry is Prevent two edges between two vertices , Between two vertices there is either

0

0

0 side , Or there is

1

1

1 side ;

Symmetry is Between any two vertices , Or there is

0

0

0 side , Or there is

2

2

2 side ;

If in the diagram , There is no edge between two vertices , Then the relationship Both symmetrical , It is also antisymmetric ; ( Rings do not affect the definitions of symmetry and antisymmetry )

5、 ... and 、 Antisymmetric example

---

Antisymmetry : There are no two sides between vertices , Only

0

0

0 side or

1

1

1 side

symmetry : There is only

0

0

0 side , or

1

1

1 side

The picture above is antisymmetric , There are two

1

1

1 side , One

0

0

0 side ;

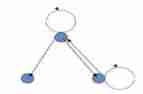
The figure above is non antisymmetric , Yes

0

0

0 side ,

1

1

1 side ,

2

2

2 The situation of the edge , Yes no antisymmetric ;

6、 ... and 、 Antisymmetry theorem

---

Antisymmetry theorem :

R

R

R It's antisymmetric

⇔

\Leftrightarrow

⇔

R

−

1

∩

R

⊆

I

A

R^{-1} \cap R \subseteq I_A

R−1∩R⊆IA​

⇔

\Leftrightarrow

⇔

R

−

1

R^{-1}

R−1 It's antisymmetric

⇔

\Leftrightarrow

⇔

M

(

R

)

M(R)

M(R) In the relation matrix ,

∀

i

∀

j

(

i

≠

j

∧

r

i

j

=

1

→

r

j

i

=

0

)

\forall i \forall j (i \not= j \land r_{ij} = 1 \to r_{ji} = 0)

∀i∀j(i​=j∧rij​=1→rji​=0)

⇔

\Leftrightarrow

⇔

G

(

R

)

G(R)

G(R) In the diagram ,

∀

a

i

∀

a

j

(

i

≠

j

)

\forall a_i \forall a_j (i \not= j)

∀ai​∀aj​(i​=j) , If there is a directed edge

<

a

i

,

a

j

>

<a_i, a_j>

<ai​,aj​> , It must not exist

<

a

j

,

a

i

>

<a_j, a_i>

<aj​,ai​>

R

−

1

∩

R

⊆

I

A

R^{-1} \cap R \subseteq I_A

R−1∩R⊆IA​ explain :

R

R

R Relationship And

R

−

1

R^{-1}

R−1 Relationship (

R

R

R The inverse of ) Intersection , Included in In the identity relationship ;

If there are two edges between two vertices , After finding the inverse , The two edges of the two vertices are opposite , Or the same two sides , If the two intersect , There are still two sides , Definitely not an identity relationship , Identity relations are rings ; ( Does not conform to anti symmetry )

If there is

1

1

1 side , After finding the inverse , There is an opposite edge between the two vertices , The intersection of the two relationships must be empty , All that remains is the ring ; ( antisymmetric )

If there is

0

0

0 side , After finding the inverse , Between the two vertices is

0

0

0 side , The intersection of the two relationships must be empty , All that remains is the ring ; ( antisymmetric )

The relational matrix :

M

(

R

)

M(R)

M(R) in ,

∀

i

∀

j

(

i

≠

j

∧

r

i

j

=

1

→

r

j

i

=

0

)

\forall i \forall j ( i \not= j \land r_{ij} = 1 \to r_{ji} = 0 )

∀i∀j(i​=j∧rij​=1→rji​=0)

The positions outside the diagonal cannot have symmetry

1

1

1 The situation of , Such as

r

i

j

=

1

r_{ij} = 1

rij​=1 , Its symmetrical elements

r

j

i

r_{ji}

rji​ It must not be

1

1

1 , Must be

0

0

0 ;

The diagram :

G

(

R

)

G(R)

G(R) in , If

∀

a

i

∀

a

j

(

i

≠

j

)

\forall a_i \forall a_j ( i \not= j )

∀ai​∀aj​(i​=j) , If there is a directed edge

<

a

i

,

a

j

>

<a_i, a_j>

<ai​,aj​> , There must be no

<

a

j

,

a

i

>

<a_j , a_i>

<aj​,ai​> ;

In the diagram Two vertices There are only one-way edges , Or no edge , There are no edges in both directions ;

7、 ... and 、 Examples of symmetry and antisymmetry

---

In the above diagram , Between two vertices

0

0

0 side ,

2

2

2 side , It's symmetrical ;

Reflexive , All vertices have rings , It's reflexive ;

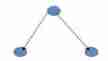
The above diagram is antisymmetric , There are A directed edge ;

All the vertices There is no ring yes Reflexive ;

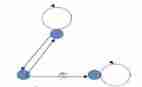
In the above figure , Some vertices have

1

1

1 side , Some vertices have

2

2

2 side , Neither symmetrical , It's not opposed ;

Some vertices have rings , Some vertices have no rings , neither Reflexive , It's not reflexive ;

In the above diagram , Between the vertices are

0

0

0 side ;

Between the vertices is

0

0

0 side /

2

2

2 side It's symmetrical ;

Between the vertices is

0

0

0 side /

1

1

1 side It's antisymmetric ;

The above diagram both symmetrical , It is also antisymmetric ;

Some vertices have rings , Some vertices have no rings , neither Reflexive , It's not reflexive ;