Eigen matrix operation Library

Catalog

1. To configure

2. initialization

2.1 Array class

2.2 Vector class

2.3 Matrix class

2.4 Vector assignment

2.5 Advanced initialization

3. Matrix computing

3.1 Matrix basic calculation

3.2 Linear solution

3.3 Eigenvalue calculation

3.4 Singular value decomposition

summary

Do scientific research projects , Especially with linear optimization , Items related to principal component analysis , It is necessary to use matrix calculation and related optimization tools . Many students will use matlab Complete the project requirements , This is certainly a good choice . however , Projects with certain requirements for the platform , Especially those based on C++ Engineering projects developed , Use matlab It will bring some inconvenience . We hope to have a convenient matrix open source tool , Can be integrated into a project , To simplify the difficulty of program deployment and use . Here we have to mention the famous matrix open source library ,Eigen. Today's blog , Let me introduce to you Eigen Basic knowledge of deployment and use , It's convenient for novice friends to quickly master based on Eigen The matrix calculation and optimization function .

---

1. To configure

First, we download it on the official website Eigen The latest version (V3.4)

3.4.0 · libeigen / eigen · GitLab

Here we use VS2022 As a development platform . The configuration is very simple , As long as VC++ The directory include add to Eigen The path can be .

  Here is a test code ：

#include <iostream>
#include <Eigen/Dense>
using namespace Eigen;
using namespace std;
typedef Eigen::Matrix<int, 3, 3> Matrix3i;

int main()
{	
    Matrix3i m1;
    m1 << 1, 2, 3, 4, 5, 6, 7, 8, 9;
    cout << "m1 = \n" << m1 << endl;
    Matrix3i m2;
    m2 << 2, 0, 0, 0, 2, 0, 0, 0, 2;
    cout << "m2 = \n" << m2 << endl;
    cout << "m1 * m2 = \n" << (m1 * m2) << endl;
    return 0;
}

Print the results ：

---

2. initialization

Finish in the configuration Eigen after , Next we want to know how to initialize vectors and matrices .Eigen Many initialization methods are supported ,  Reference blog Eigen Summary of library usage ,Eigen Library usage ,Eigen initialization , We list several for reference ：

2.1 Array class

Direct assignment

Eigen::Array<int, 3, 1> arr_1(1, 2, 3);

Stream input assignment

Eigen::Array<int, 3, 3> arr_2;
    arr_2 <<
        1, 2, 3,
        4, 5, 6,
        7, 8, 9;

Pointer assignment

std::vector<int> vec_int{ 1,2,3,4,5,6,7,8,9 };
    Eigen::Array<int, 3, 3> arr_3(vec_int.data());

2.2 Vector class

Vector The assignment method of is the same as Array Basically the same .Vector Can be seen as a special Matrix.

Eigen::Vector3f v1 = Eigen::Vector3f::Zero();

Eigen::Vector3d v2(1.0, 2.0, 3.0);

Eigen::VectorXf v3(20); // Dimension for 20 Vector , uninitialized .
v3 << 1.0 , 2.0 , 3.0;

2.3 Matrix class

And Array The initialization method of is basically the same

Eigen::Matrix<double,2,2> m;
m << 1,2,3,4;

Eigen::MatrixXf m1(2,3);
m1 << 1,2,3,
	  4,5,6;

Eigen::Matrix3d m2 = Eigen::Matrix3d::Identity();//Eigen::Matrix3d::Zero();

Eigen::Matrix3d m3 = Eigen::Matrix3d::Random(); // Random initialization 

2.4 Vector assignment

sometimes , We will store the data in C++ Data structure of vector in . here , We hope that vector The data is converted into a matrix , And make corresponding calculation . In addition to using pointers , We can also directly vector The data is copied into the matrix .

std::vector<std::vector<double>> LX;
MatrixXd m_Lx(LX.size(), 3);	
for (int i = 0; i < LX.size(); i++) {
	m_Lx(i, 0) = LX[i][0];
	m_Lx(i, 1) = LX[i][1];
	m_Lx(i, 2) = LX[i][2];
}

hypothesis LX It is a point cloud data , Each point is a three-dimensional vector . Corresponding to the established MatrixXd m_LX I.e LX Have the same dimension , the C++ Of vector Convert to eigen Of matrix.

2.5 Advanced initialization

Reference resources matlab,eigen It also provides some advanced data initialization methods with rich functions , Including independent assignment of row and column vectors , Block assignment, etc . Here are some sample code , For reference .

Column vector assignment

RowVectorXd rv1(1,2,3);

Block assignment

Yes m4 Calculate , And assign values to m5, Output m5： 

MatrixXf m4(2,2);
m4 << 1,2,3,4;
MatrixXf m5(4,4);
m5 << m4, m4 / 10, m4 * 10, m4;// take m5 It is divided into four parts for assignment 

More accurate assignment , First enter the first line : 1, 2, 3; And then according to block Information about , In the second row of the matrix , Insert a... In the first column 2*2 The submatrix of ,4, 5, 6, 7; Last , In the third column , The last two positions tail(2), Insert 6, 9. You can see , The above operation realizes the accurate assignment of a matrix block .

Matrix3f m;
m.row(0) << 1,2,3;
m.block(1,0,2,2) << 4,5,6,7; 
m.col(2).tail(2) << 6,9;

---

3. Matrix computing

Based on the assigned matrix , We hope to pass Eigen Realize the calculation of the matrix . Here we divide the matrix calculation into three parts , Including basic matrix calculation , Linear solution , Eigenvalue calculation and singular value decomposition .

3.1 Matrix basic calculation

The basic calculation of matrix is relatively simple , Including plus , reduce , Cross riding , Point multiplication , Transposition , Inverse, etc .

MatrixXf m = MatrixXf::Random(3,3);
MatrixXf m2 = MatrixXf::Random(3,3);
m.row(i);// Matrix No i That's ok 
m.col(j);// Matrix No j Column 
m.transpose();// Transposition 
m.conjugate();// conjugate 
m.adjoint(); // Conjugate transpose 
m.minCoeff();// The smallest of all elements 
m.maxCoeff();// The largest of all elements 
m.trace();// trace , Sum of diagonal elements 
m.sum(); // Sum all the elements 
m.prod(); // Quadrature of all elements 
m.mean(); // Average all elements 
m.dot(m2); // Point multiplication 
m.cross(m2);// Cross riding 

3.2 Linear solution

solve Ax=b,eigen Several tools are provided , Include ：

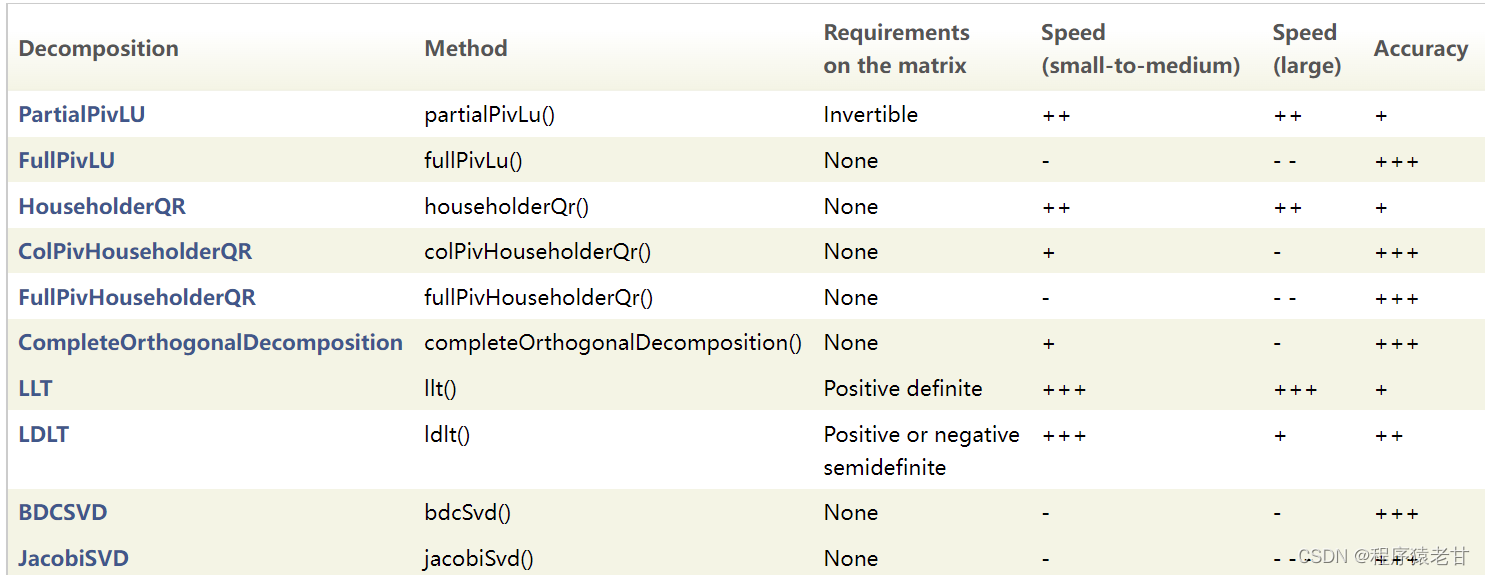
  Generally, people will choose LLT and LDLT

 Eigen::Matrix2f A, b;
 A << 2, -1, -1, 3;
 b << 1, 2, 3, 1;
 std::cout << "Here is the matrix A:\n" << A << std::endl;
 std::cout << "Here is the right hand side b:\n" << b << std::endl;
 Eigen::Matrix2f x = A.ldlt().solve(b);//or A.llt().solve(B);                   
 std::cout << "The solution is:\n" << x << std::endl;

3.3 Eigenvalue calculation

Eigenvalue and corresponding eigenvector calculation , It plays an important role in matrix analysis . be based on Eigen The eigenvalues of are calculated as follows ：

Eigen::MatrixXd m = Eigen::MatrixXd::Random(3,3);
Eigen::MatrixXd mTm = m.transpose() * m;// Constitute the covariance matrix of the center 

// Calculation 
Eigen::SelfAdjointEigenSolver<Eigen::MatrixXd> eigen_solver(mTm);

// Extract eigenvalues and eigenvectors 
Eigen::VectorXd eigenvalues = eigen_solver.eigenvalues();
Eigen::MatrixXd eigenvectors = eigen_solver.eigenvectors();

Eigen::VectorXd v0 = eigenvectors.col(0);//  Because the eigenvalues are generally arranged from small to large , therefore col(0) Is the eigenvector corresponding to the minimum eigenvalue 

3.4 Singular value decomposition

Reference blog ： Introduction to matrix singular value decomposition

Singular value decomposition (singular value decomposition, SVD)： Decompose a matrix into singular vectors (singular vector) And singular value (singular value). Through singular value decomposition , We will get some information of the same type as feature decomposition . However , Singular value decomposition has a wider range of applications . Every real matrix has a singular value decomposition , But not all of them have eigendecomposition . for example , The matrix of a non square matrix has no characteristic decomposition , We can only use singular value decomposition .

The matrix A Decomposing into the product of three matrices ：A=UDV^T.

Each of these matrices has a special structure after being defined . matrix U and V Are defined as orthogonal matrices , And matrix D Is defined as a diagonal matrix . Be careful , matrix D It doesn't have to be a square . Diagonal matrix D Elements on the diagonal are called matrices A The singular value of (singular value). matrix U The column vector of is called the left singular vector (left singular vector), matrix V The column vector of is called the right singular vector (right singular vector).A The left singular vector of is AA^T Eigenvector of .A The right singular vector of is A^TA Eigenvector of .A The nonzero singular value of is A^TA Square root of eigenvalue , It's also AA^T Square root of eigenvalue .

JacobiSVD<MatrixXd> svd(J, ComputeThinU | ComputeThinV);
U = svd.matrixU();
V = svd.matrixV();
D_t = svd.singularValues();

---

summary

Based on C++ Matrix operation library ,Eigen Simple deployment , High execution efficiency , It integrates matrix operation functions with rich functions . master Eigen, It can significantly improve the efficiency of solving matrix optimization problems .