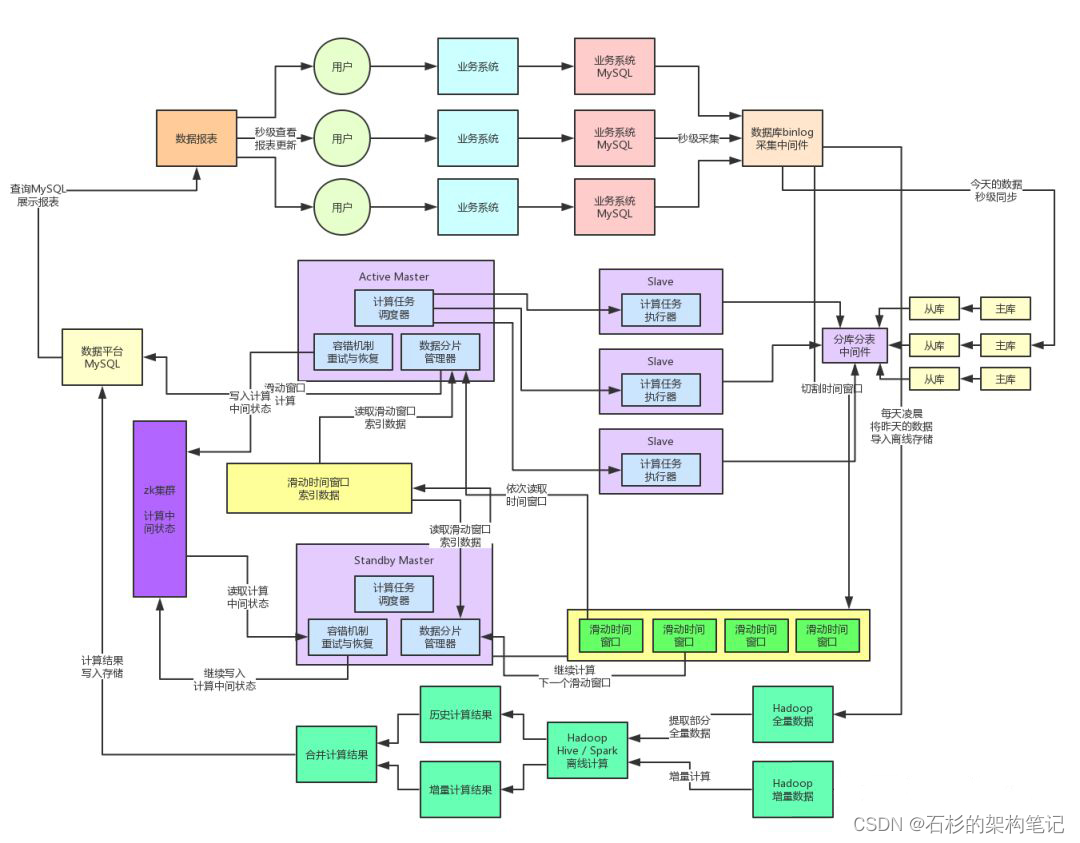
图论-虚拟节点分层建图
Nya图最短路
题目链接:Virtual JudgeAcwing
题意:
题解:\(a,b\)连一个\(w\)的边,是正常操作,这里有一个重要操作是\(a\)层和\(a+1\)层能直接传送,如果这里使用笨笨的建图方式,那么时间复杂度就是\(O(n^2)\),时间复杂度太高,不太行.
这里有一个聪明的建图方法--->虚拟节点分层建图 具体表示为:将\(a\)层和\(a+1\)层中间建立一个虚拟节点,然后将\(a\)层的所以节点指向虚拟节点,然后虚拟节点指向\(a+1\)层,这样就能实现在\(O(n)\)的时间复杂度情况下进行建图,时间可以接受 具体可以看图: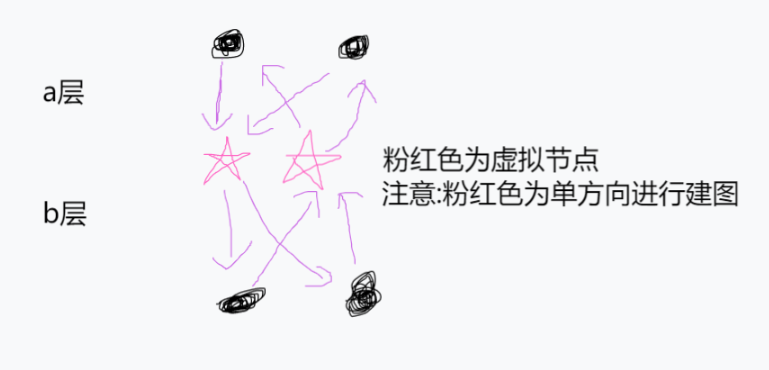
code
#include <bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
#define eps 1e-8
#define int128 __int128
#define gcd(a,b) __gcd(a,b)
#define lcm(a,b) a/gcd(a,b)*b
#define lowbit(x) (x&-x)
#define all(x) x.begin(), x.end()
#define debug(x...) do { cout<< #x <<" -> "; re_debug(x); } while (0)
void re_debug() { cout<<'\n'; }
template<class T, class... Ts> void re_debug(const T& arg,const Ts&... args) { cout<<arg<<" "; re_debug(args...); }
void cut(){ cout<<'\n'<<"------------"<<'\n';}
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> PII;
const int INF=0x3f3f3f3f;
const ll LNF=0x3f3f3f3f3f3f3f3f;
const double PI=acos(-1.0);
const int N=2e5*3;
int e[N],ne[N],h[N],idx;
int w[N];
int dist[N];
int n,m,c;
int t=1;
bool st[N];
void add(int a,int b,int c)
{
e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}
void dijkstra()
{
priority_queue<PII,vector<PII>,greater<PII>> q;
q.push({0,1});
dist[1]=0;
while(q.size())
{
auto v=q.top().second;
q.pop();
if(st[v]) continue;
st[v]=true;
for(int i=h[v];i!=-1;i=ne[i])
{
int j=e[i];
if(dist[j]>dist[v]+w[i])
{
dist[j]=dist[v]+w[i];
q.push({dist[j],j});
}
}
}
}
void solve()
{
idx=0;//注意一定要清零
scanf("%d%d%d",&n,&m,&c);
for(int i=0;i<=n*3;i++)//用到了3n这些点
{
dist[i]=INF;
st[i]=0;
h[i]=-1;
}
vector<vector<int>> depth(n+1+1);
int max_depth=-1;
for(int i=1;i<=n;i++)
{
int x;
scanf("%d",&x);
depth[x].push_back(i);
max_depth=max(max_depth,x);
}
for(int i=1;i<max_depth;i++)
{
//这里用到了3*n以上的点,其实n--2n这一层是a层-->a+1层,2n--3n是a+1到a层,注意这是单向边
for(auto &t:depth[i]) add(t,n+i+1,c);//t层连到t+1层
for(auto &t:depth[i+1]) add(n+i+1,t,0);/
for(auto &t:depth[i]) add(2*n+i+1,t,0);
for(auto &t:depth[i+1]) add(t,2*n+i+1,c);
}
for(int i=0;i<m;i++)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c);
add(b,a,c);
}
dijkstra();
if(dist[n]==INF) printf("Case #%d: %d\n",t++,-1);
else printf("Case #%d: %lld\n",t++,dist[n]);
}
int main()
{
int T=1;
scanf("%d",&T);
while(T--) solve();
return (0^0);
}
Slipper
杭电多校第四场第三题,其实这里就是n层能跳到n+k层了,那么其实就是板子了
#include <bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
#define eps 1e-8
#define int128 __int128
#define gcd(a,b) __gcd(a,b)
#define lcm(a,b) a/gcd(a,b)*b
#define lowbit(x) (x&-x)
#define all(x) x.begin(), x.end()
#define debug(x...) do { cout<< #x <<" -> "; re_debug(x); } while (0)
void re_debug() { cout<<'\n'; }
template<class T, class... Ts> void re_debug(const T& arg,const Ts&... args) { cout<<arg<<" "; re_debug(args...); }
void cut(){ cout<<'\n'<<"------------"<<'\n';}
typedef long long ll;
typedef unsigned long long ull;
typedef pair<ll,int> PII;
const int INF=0x3f3f3f3f;
const ll LNF=0x3f3f3f3f3f3f3f3fll;
const double PI=acos(-1.0);
const int N=2000010*4;
int e[N],ne[N],w[N],h[N],idx;
int depth[N];
ll dist[N];
bool st[N];
int n;
int max_depth=-1;
int s,t;
void add(int a,int b,int c)
{
e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}
void dfs(int u,int father)//处理出来这个深度
{
depth[u]=depth[father]+1;
max_depth=max(max_depth,depth[u]);
for(int i=h[u];i!=-1;i=ne[i])
{
int j=e[i];
if(j==father) continue;
dfs(j,u);
}
}
void dijkstra()
{
priority_queue<PII,vector<PII>,greater<PII>> q;
dist[s]=0;
q.push({0,s});
while(q.size())
{
auto v=q.top().second;q.pop();
if(st[v]) continue;
st[v]=true;
for(int i=h[v];i!=-1;i=ne[i])
{
int j=e[i];
if(dist[j]>dist[v]+w[i])
{
dist[j]=dist[v]+w[i];
q.push({dist[j],j});
}
}
}
}
void solve()
{
idx=0;
cin>>n;
for(int i=0;i<=n*3+10;i++)
{
h[i]=-1;
dist[i]=LNF;
st[i]=0;
}
for(int i=0;i<n-1;i++)
{
int a,b,c;
cin>>a>>b>>c;
add(a,b,c);
add(b,a,c);
}
int k,p;
cin>>k>>p;
dfs(1,-1);
vector<vector<int>> depths(max_depth+k+1);
for(int i=1;i<=n;i++)
{
depths[depth[i]].push_back(i);
}
for(int i=1;i<=max_depth;i++)
{
for(auto &t:depths[i]) add(t,n+i+1,p);//t层连到t+k层
for(auto &t:depths[i+k]) add(n+i+1,t,0);//注意不要重复
for(auto &t:depths[i]) add(2*n+i+1,t,0);
for(auto &t:depths[i+k]) add(t,2*n+i+1,p);
}
cin>>s>>t;
dijkstra();
if(dist[t]==LNF) cout<<"-1"<<'\n';
else cout<<dist[t]<<'\n';
}
int main()
{
IOS;
int T=1;
cin>>T;
while(T--) solve();
return 0^0;
}