当前位置:网站首页>牛客2022 暑期多校3 H Hacker(SAM + 线段树查询区间内部最大子段和)
牛客2022 暑期多校3 H Hacker(SAM + 线段树查询区间内部最大子段和)
2022-08-03 22:50:00 【Morgannr】
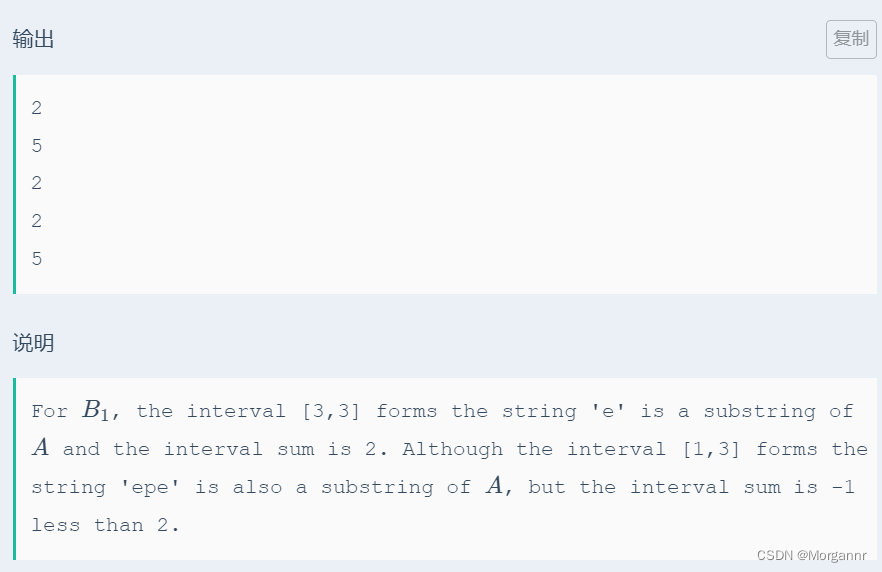
题意:
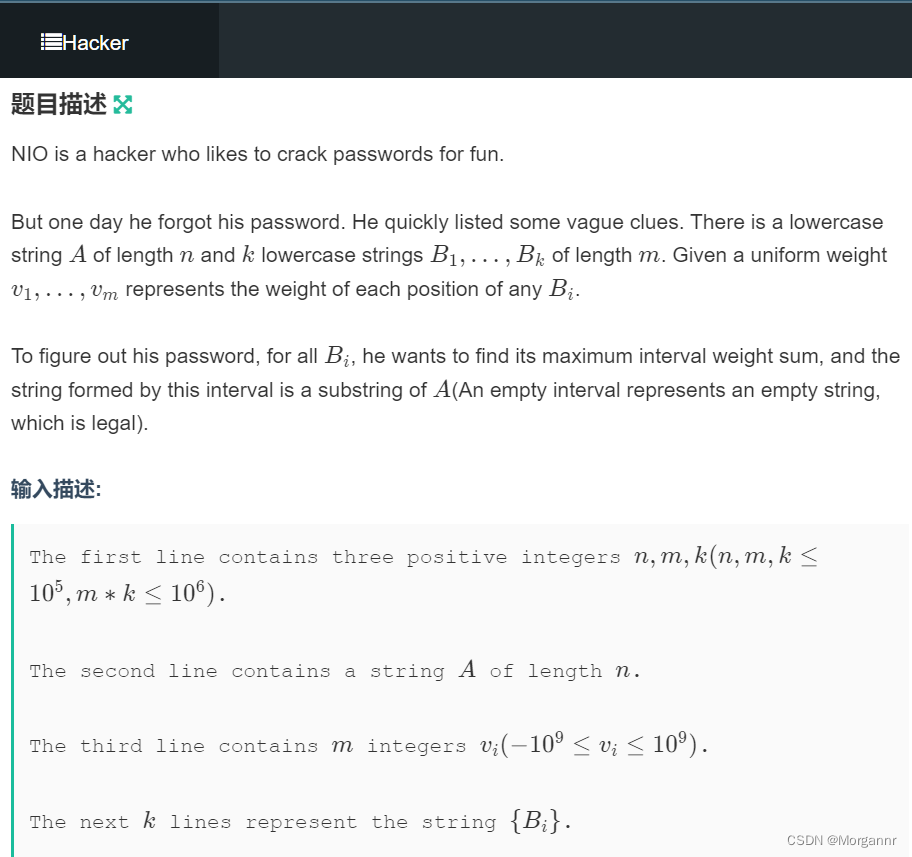
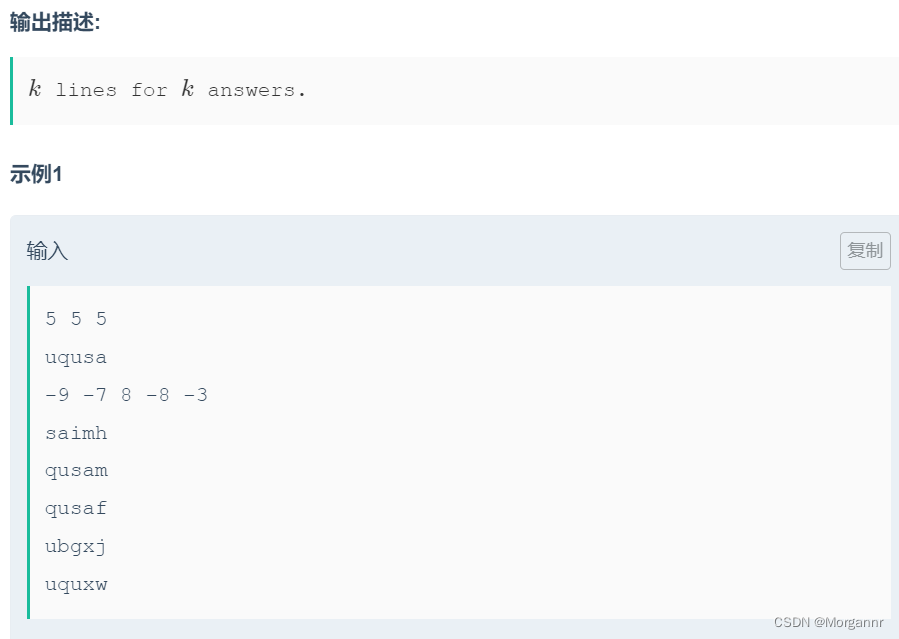
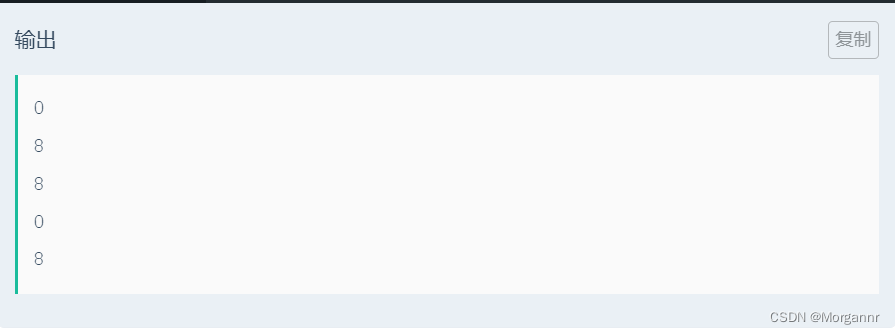
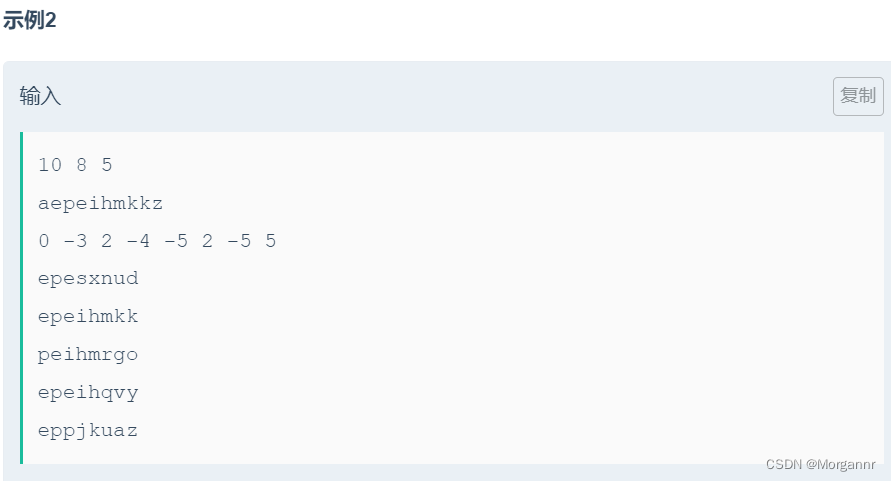
给定 主串 以及 若干副串,副串长度固定,每个位置 都有一个 权值,要求在 主串和副串的公共子串中 找到一个 连续区间,使得 连续区间的权值和最大,求 最大权值和。
思路:
本题其实就是 这两道板子题:SPOJ 2774 Longest Common Substring 和 AcWing 245. 你能回答这些问题吗 硬生生的结合版,
用 SAM 维护 主串 和 枚举的各个副串 的 所有公共子串,对于 主串 与 某个副串 的 某个公共子串所在区间,我们利用 线段树 维护 区间内部最大子段和 即可。
简单题,但是比赛的时候由于没学 SAM 而寄了
不过值得一提的是,代码中的将 主串 和 副串 的 所有公共子串所在区间 提取出来的操作:
int p = 1, t = 0;
for (int j = 1; ss[j]; ++j) {
int sta, ed; //存储每个公共子串所在的合法区间左右端点
int c = ss[j] - 'a';
while (p > 1 && !ch[p][c]) {
//经典匹配操作
p = fa[p];
t = len[p];
}
ed = j - 1; //此时由于当前字符s[j]还未匹配,因此右端点为j-1
if (ch[p][c]) {
//如果当前字符s[j]匹配成功,则右端点移至j,且LCS的长度t++
p = ch[p][c];
++t;
++ed;
}
if (t) {
//当前公共子串长度不为0,即合法,根据其长度t计算左端点sta(因为右端点ed已经求出,相减即可)
sta = ed - t + 1;
}
}
时间复杂度:
O ( n l o g n ) O(nlogn) O(nlogn)
代码:
#include <bits/stdc++.h>
using namespace std;
//#define map unordered_map
#define int long long
int n, m, k;
const int N = 1e5 + 10, M = N << 1;
int fa[M], ch[M][26], len[M], cnt[M];
int np = 1, tot = 1;
char s[N], ss[N];
int w[N];
struct node {
int l, r;
int tmax, sum, lmax, rmax;
} t[N << 2];
void pushup(node& u, node& l, node& r) {
u.sum = l.sum + r.sum;
u.tmax = max(max(l.tmax, r.tmax), l.rmax + r.lmax);
u.lmax = max(l.lmax, l.sum + r.lmax);
u.rmax = max(r.rmax, r.sum + l.rmax);
}
void pushup(int u) {
pushup(t[u], t[u << 1], t[u << 1 | 1]);
}
void build(int u, int l, int r) {
t[u] = {
l, r };
if (l == r) {
t[u].tmax = t[u].sum = t[u].lmax = t[u].rmax = w[l];
return;
}
int mid = l + r >> 1;
build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
pushup(u);
}
node ask(int u, int l, int r) {
if (l <= t[u].l && r >= t[u].r) return t[u];
int mid = t[u].l + t[u].r >> 1;
if (r <= mid) return ask(u << 1, l, r);
else if (l >= mid + 1) return ask(u << 1 | 1, l, r);
else {
auto left = ask(u << 1, l, r);
auto right = ask(u << 1 | 1, l, r);
node res;
pushup(res, left, right);
return res;
}
}
void extend(int c) {
int p = np;
np = ++tot;
len[np] = len[p] + 1, cnt[np] = 1;
while (p && !ch[p][c]) {
ch[p][c] = np;
p = fa[p];
}
if (!p) {
fa[np] = 1;
}
else {
int q = ch[p][c];
if (len[q] == len[p] + 1) {
fa[np] = q;
}
else {
int nq = ++tot;
len[nq] = len[p] + 1;
fa[nq] = fa[q], fa[q] = fa[np] = nq;
while (p && ch[p][c] == q) {
ch[p][c] = nq;
p = fa[p];
}
memcpy(ch[nq], ch[q], sizeof ch[q]);
}
}
}
signed main()
{
cin >> n >> m >> k;
cin >> s + 1;
for (int i = 1; i <= n; ++i) {
extend(s[i] - 'a');
}
for (int i = 1; i <= m; ++i) {
scanf("%lld", &w[i]);
}
build(1, 1, m);
for (int i = 0; i < k; ++i) {
scanf("%s", ss + 1);
int p = 1, t = 0;
int res = -2e18;
for (int j = 1; ss[j]; ++j) {
int sta, ed;
int c = ss[j] - 'a';
while (p > 1 && !ch[p][c]) {
p = fa[p];
t = len[p];
}
ed = j - 1;
if (ch[p][c]) {
p = ch[p][c];
++t;
++ed;
}
if (t) {
sta = ed - t + 1;
res = max(max(res, ask(1, sta, ed).tmax), (int)0);
}
}
printf("%lld\n", res);
}
return 0;
}
边栏推荐
- Basic Concepts of Graphs
- 获国际权威认可 | 云扩科技入选《RPA全球市场格局报告,Q3 2022》
- 优化查询(工作中)
- 软测人每个阶段的薪资待遇,快来康康你能拿多少?
- Create function report error, prompting DECLARE definition syntax problem
- Golang Chapter 1: Getting Started
- 113. Teach a Man how to fish - How to query the documentation and technical implementation details of any SAP UI5 control property by yourself
- 一个函数有多少种调用方式?
- October 2019 Twice SQL Injection
- Golang第二章:程序结构
猜你喜欢

noip preliminary round
2022的七夕,奉上7个精美的表白代码,同时教大家快速改源码自用

软测人每个阶段的薪资待遇,快来康康你能拿多少?
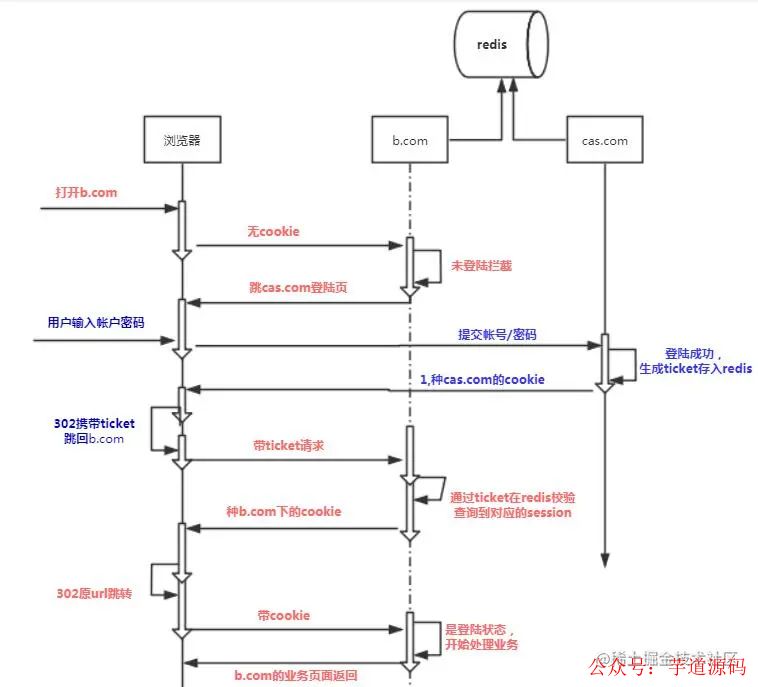
Boss: There are too many systems in the company, can you realize account interoperability?
PowerMockup 4.3.4::::Crack
Embedded Systems: GPIO
Click the icon in Canvas App to generate PDF and save it to Dataverse
七夕活动浪漫上线,别让网络拖慢和小姐姐的开黑时间
LabVIEW code generation error 61056
V8中的快慢数组(附源码、图文更易理解)
随机推荐
The sword refers to the offer question 22 - the Kth node from the bottom in the linked list
Storage engine written by golang, based on b+ tree, mmap
重发布实验报告
Pytest learn-setup/teardown
Golang Chapter 1: Getting Started
冰河又一MySQL力作出版(文末送书)!!
Causes of Mysql Disk Holes and Several Ways to Rebuild Tables
Makefile
走迷宫 BFS
封装、包、访问权限修饰符、static变量
"Digital Economy Panorama White Paper" Financial Digital User Chapter released!
log4j-slf4j-impl cannot be present with log4j-to-slf4j
斩获双奖|易知微荣获“2021中国数字孪生解决方案优秀供应商”“中国智能制造优秀推荐产品”双奖项!
【day6】类与对象、封装、构造方法
What is Adobe?
node连接mysql数据库报错:Client does not support authentication protocol requested by server
Boss: There are too many systems in the company, can you realize account interoperability?
目标检测的国内外研究现状
Republish the lab report
With 4 years of work experience, the 5 communication methods between multi-threads can't be said, can you believe it?