Bayesian inference problem, MCMC and variational inference

The Bayesian inference problem

What is Bayesian inference?

• 簡單來說，貝葉斯推理就是基於貝葉斯範式進行統計推理。貝葉斯範式的基本思想就是利用貝葉斯定理來錶達後驗知識 $p(\theta |x)$ (the “posterior”)、先驗知識 $p(\theta )$ (the “prior”) 和似然 $p(x|\theta )$ (the “likelihood”) 之間的關系
  

Computational difficulties

• 在很多場景下，prior 和 likelihood 都是已知的，但歸一化因子 evidence 卻需要通過積分得到：
  上述積分在高維情况下將變得難以解决，因此需要使用一些近似方法去估計後驗概率
• 常用的近似方法有 Markov Chain Monte Carlo 和 Variational Inference (one should keep in mind that these methods can also be precious when facing other computational difficulties related to Bayesian inference)

Markov Chains Monte Carlo (MCMC) – A sampling based approach

• 馬爾可夫鏈蒙特卡羅法 (Markov Chain Monte Carlo, MCMC) (MCMC 對待采樣概率分布是否歸一化並不敏感，即使不進行歸一化也可以對其進行采樣)
  

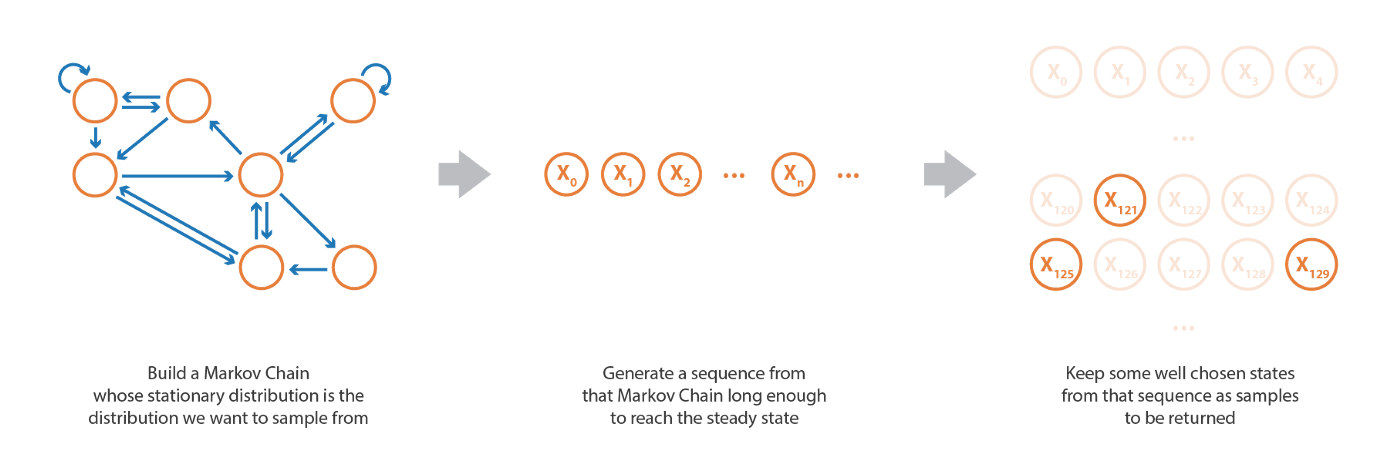
Variational Inference (VI) – An approximation based approach

The approximation approach

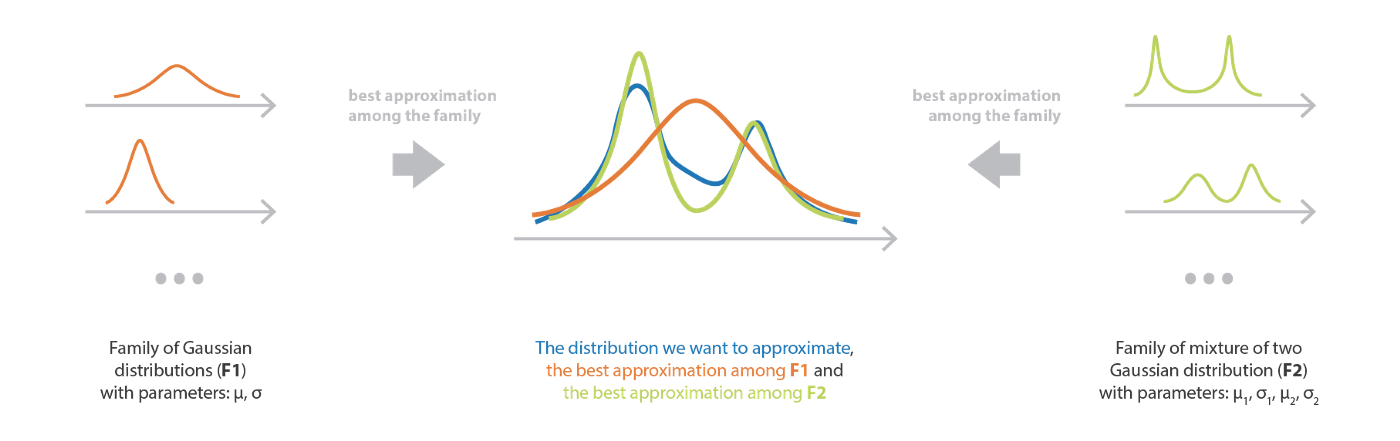
• 與 MCMC 基於馬爾可夫鏈進行采樣不同，變分推理旨在從指定的概率分布族中找到複雜待采樣概率分布的一個最佳近似概率分布，實際上就是解决一個優化問題
• 具體而言，首先需要定義一個參數化的概率分布族，其中的不同概率分布由相應的參數决定 (e.g. 正態分布由 $\mu$ 和 $\sigma$ 控制)
  然後需要從 $F_{\Omega }$ 中找到一個最接近待采樣概率分布的概率分布 ${\omega }^{\ast }$，也就是解如下最優化問題：
  其中，$\pi$ 為待采樣概率分布，$E(p,q)$ 用於衡量兩個概率分布之間的距離。在變分推理中，$E(p,q)$ 為 KL 散度，優化過程采用梯度下降 (由於 KL 散度對 $p$ 是否歸一化不敏感，因此變分推理不要求對待采樣概率分布進行歸一化)
  

Family of distribution

• 概率分布族的選擇實際上是一個非常强的先驗信息，它决定了對待采樣概率分布近似的 bias 以及優化過程的複雜度。如果分布族過於簡單，那麼近似的 bias 就會特別大，但優化過程很簡單，反之 bias 會較小，但優化過程就比較複雜。因此，我們有必要維持好 bias 和複雜度之間的平衡
  

---

平均場變分族 (mean-field variational family)

• 在平均場變分族中，隨機向量的所有分量都是獨立的，因此概率密度函數可以寫為下式：
  其中，$z$ 為 $m$ 維的隨機向量，$f_j$ 為 $z$ 的第 $j$ 個分量的概率密度函數

Kullback-Leibler divergence

• 在尋找待采樣概率分布的近似分布時，我們希望該優化過程對歸一化因子不敏感，而使用 KL 散度作為度量標准可以很好地滿足這一條件。設 $\pi$ 為待采樣概率分布，$C$ 為歸一化因子
  則
  因此在使用 KL 散度作為度量標准時，優化過程對歸一化因子不敏感，我們不必對待采樣概率進行歸一化：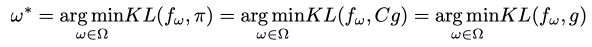
  

Optimisation process and intuition

• 上述最優化問題可以利用梯度下降等方法尋找最優解

---

Intuition

• 為了更好地理解上述優化過程，下面以貝葉斯推理為例進行說明：
  從最後一項中可以看到，最佳近似後驗概率分布會使得基於觀測數據 $x$ 的期望對數似然盡量大，同時使得該近似後驗分布與先驗分布之間的 KL 散度盡量小 (prior/likelihood balance)

MCMC v.s. VI

• MCMC 和 VI 有著不同的應用場合。一方面，MCMC 的采樣過程計算量較大但 bias 較小，因此適用於需要得到精准結果而不在乎時間開銷的場合。另一方面，VI 中概率分布族的選擇和優化過程均會引入了 bias，相比 MCMC 而言 bias 較大但計算開銷較小，因此適用於需要快速計算的大規模推理問題

References

• Bayesian inference problem, MCMC and variational inference
• more about VI: Variational Inference: A Review for Statisticians
• more about MCMC: Introduction to Markov Chain Monte Carlo、An Introduction to MCMC for Machine Learning
• more about Gibbs Sampling applied to LDA: Tutorial on Topic Modelling and Gibbs Sampling、lecture note on LDA Gibbs Sampler