当前位置:网站首页>Notes on Combinatorics (V) chains in distributive lattice
Notes on Combinatorics (V) chains in distributive lattice
2022-06-22 19:21:00 【zorchp】
tags: Combinatorics
Write it at the front
This part is mainly the third part of combinatorics of numbers 3.5 and 3.6 Section content .
Simple properties of distributive lattices
Easy to verify :
- P P P Of k k k The number of ordered ideals is equal to J ( P ) J(P) J(P) The middle rank is k k k Number of elements of .
- P P P in k k k Meta inverse chain ( k ≥ 1 ) (k≥1) (k≥1) The number of is equal to J ( P ) J(P) J(P) Which just covers k k k Number of elements of elements
proposition 1
set up P P P Is a finite poset and m ∈ N m ∈ \mathbb N m∈N, Is the following number equal :
- Order preserving mapping σ : P → m σ:P→\bf m σ:P→m The number of ,
- J ( P ) J(P) J(P) The medium length is m m m The heavy chain of 0 ^ = I 0 ≤ I 1 ≤ ⋅ ⋅ ⋅ ≤ I m = 1 ^ \hat0=I_0 ≤I_1 ≤···≤I_m =\hat1 0^=I0≤I1≤⋅⋅⋅≤Im=1^ The article number ,
- J ( P × m − 1 ) J(P×{\bf m−1}) J(P×m−1) The number of elements in .
prove : ( Constructive bijection )
σ : P → m σ:P→\bf m σ:P→m,( Posets P P P To m m m Mapping of meta chains ) Definition I j = σ − 1 ( j ) I_j=\sigma^{-1}({\bf j}) Ij=σ−1(j), Given 0 ^ = I 0 ≤ I 1 ≤ ⋅ ⋅ ⋅ ≤ I m = 1 ^ \hat0=I_0 ≤I_1 ≤···≤I_m =\hat1 0^=I0≤I1≤⋅⋅⋅≤Im=1^, Definition J ( P × m − 1 ) J(P×{\bf m−1}) J(P×m−1) The order ideal of is
I = { ( x , y ) ∈ P × m − 1 : x ∈ I m − j } , I=\{(x,y)\in P×{\bf m−1}:\ x\in I_{m-j}\}, I={ (x,y)∈P×m−1: x∈Im−j},
Define the above σ \sigma σ by : If there is j j j bring ( x , j ) ∈ I (x,j)\in I (x,j)∈I, be σ ( x ) = min { m − j : ( x , j ) ∈ I } \sigma(x)=\min\{m-j:\ (x,j)\in I\} σ(x)=min{ m−j: (x,j)∈I}, If it does not exist , be σ ( x ) = m \sigma(x)=m σ(x)=m. This constitutes a bijection satisfying the above condition . Or directly by 1 , 3 1,3 1,3 obtain :
m P ≅ ( 2 m − 1 ) P ≅ 2 m − 1 × P . {\mathbf m}^P\cong({\bf 2^{m-1}})^P\cong {\bf2}^{ {\bf m-1}\times P}. mP≅(2m−1)P≅2m−1×P.
proposition 2
set up P P P Is a finite poset and m ∈ N m ∈ \mathbb N m∈N, Is the following number equal :
- Order preserving surjection σ : P → m σ:P→\bf m σ:P→m The number of ,
- J ( P ) J(P) J(P) The medium length is m m m Chain 0 ^ = I 0 < I 1 < ⋅ ⋅ ⋅ < I m = 1 ^ \hat0=I_0 <I_1 <···<I_m =\hat1 0^=I0<I1<⋅⋅⋅<Im=1^ The article number .
- P P P Extension to total order ( P P P Linear extension of ): If ∣ P ∣ = n |P|=n ∣P∣=n, Then order preserving bijection σ : P → n \sigma:P\to {\bf n} σ:P→n.
- Number of expansions Write it down as e ( P ) e(P) e(P), It's obviously equal to J ( P ) J(P) J(P) The number of middle maximal chains .
Distributive lattice and lattice count
Can be P P P Extension to total order σ : P → n \sigma:P\to\bf n σ:P→n Equate to P P P Arrangement of elements in : σ − 1 ( 1 ) , . . . , σ − 1 ( n ) \sigma^{-1}(1),...,\sigma^{-1}(n) σ−1(1),...,σ−1(n), Or will J ( P ) J(P) J(P) The maximal chain of is equivalent to that in the following Euclidean space " grue ".
hypothesis C 1 , C 2 , ⋯ , C k C_1,C_2,\cdots,C_k C1,C2,⋯,Ck by P P P A chain partition of , (Dilworth The theorem infers that k k k The minimum possible value of is P P P The maximum cardinality of the anti chain of ), Define mapping δ : J ( P ) → N k \delta:\ J(P)\to \mathbb{N}^k δ: J(P)→Nk , δ ( I ) = ( ∣ I ∩ C 1 ∣ , ∣ I ∩ C 2 ∣ , ⋯ , ∣ I ∩ C k ∣ ) \delta(I)=(|I\cap C_1|,|I\cap C_2|,\cdots,|I\cap C_k|) δ(I)=(∣I∩C1∣,∣I∩C2∣,⋯,∣I∩Ck∣).
give N k \mathbb{N}^k Nk Product order , be δ \delta δ Is a simple lattice homomorphism , And maintain the coverage relationship , ( J ( P ) J(P) J(P) Isomorphism N k \mathbb{N}^k Nk) A sub lattice of , If you select each ∣ C i ∣ = 1 |C_i|=1 ∣Ci∣=1, A rank preserving simple lattice homomorphism is obtained J ( P ) → B n J(P)\to B_n J(P)→Bn, In the area ∣ P ∣ = n |P|=n ∣P∣=n.)
Given δ : J ( P ) → N k \delta:\ J(P)\to \mathbb{N}^k δ: J(P)→Nk, Definition Γ δ = ⋃ T c x ( δ ( T ) ) \Gamma_\delta=\bigcup_T cx(\delta(T)) Γδ=⋃Tcx(δ(T)), among c x cx cx Express R k \mathbb{R}^k Rk The convex hull in T T T Take over J ( P ) J(P) J(P) Is isomorphic to the interval of Boolean algebra . Γ δ \Gamma_\delta Γδ yes R k \mathbb{R}^k Rk A compact polyhedron subset of .
J ( P ) J(P) J(P) The number of longest chains in is equal to at Γ δ \Gamma_\delta Γδ From the origin ( 0 , 0 , . . . , 0 ) = δ ( 0 ^ ) (0,0,...,0)=\delta(\hat0) (0,0,...,0)=δ(0^) To δ ( 1 ^ ) \delta(\hat1) δ(1^) The number of lattice paths , Each step moves one unit along the axis .
namely , Number of expansions e ( P ) e(P) e(P) Equal to δ ( 1 ^ ) \delta(\hat1) δ(1^) Expressed as δ ( 1 ^ ) = v 1 + v 2 + ⋯ + v n \delta(\hat1)=v_1+v_2+\cdots+v_n δ(1^)=v1+v2+⋯+vn The number of ways , Each of them v i v_i vi Is in R k \mathbb R^k Rk A unit vector in , And for all i i i, Yes ∑ k = 1 i v k ∈ Γ δ \sum_{k=1}^iv_k\in \Gamma_\delta ∑k=1ivk∈Γδ.
example 1:( Do not hand in and ) concrete problems
For the following poset , take C 1 = { a , c } , C 2 = { b , d , e } C_1=\{a,c\}, C_2=\{b,d,e\} C1={ a,c},C2={ b,d,e}.

Use the method in the previous section , It is easy to find J ( P ) J(P) J(P), As shown in the figure below , Marked the element :

Mark with the above coordinates , You can get :

In the figure: ∅ \varnothing ∅ To a b c d e abcde abcde, From ( 0 , 0 ) (0,0) (0,0) To ( 2 , 3 ) (2,3) (2,3), Yes 9 9 9 An alternative way , therefore e ( P ) = 9 e(P)=9 e(P)=9.
example 2:( Do not hand in and ) A general example
set up P = C 1 + C 2 P=C_1+C_2 P=C1+C2, And ∣ C 1 ∣ = m , ∣ C 2 ∣ = n |C_1|=m,|C_2|=n ∣C1∣=m,∣C2∣=n, be Γ δ \Gamma_\delta Γδ For one m × n m\times n m×n Rectangular mesh , therefore e ( P ) = ( m + n n ) e(P)=\binom{m+n}n e(P)=(nm+n), From the perspective of linear order expansion , structure σ : P → m + n \sigma:\ P\to \bf m+n σ: P→m+n, Completely by σ ( C 1 ) \sigma(C_1) σ(C1) determine , by m + n \bf m+n m+n Arbitrarily m m m Meta subset , From this, we can get e ( P ) = ( m + n m ) e(P)=\binom{m+n}m e(P)=(mm+n).
Extension :
If P = P 1 + ⋯ + P k , n i = ∣ P i ∣ P=P_1+\cdots+P_k,n_i=|P_i| P=P1+⋯+Pk,ni=∣Pi∣, be
e ( P ) = ( n 1 + ⋯ + n k n 1 , ⋯ , n k ) e ( P 1 ) ⋯ e ( P k ) . e(P)=\binom{n_1+\cdots+n_k}{n_1,\cdots,n_k}e(P_1)\cdots e(P_k). e(P)=(n1,⋯,nkn1+⋯+nk)e(P1)⋯e(Pk).
example 3: ( The cartesian product )
set up P = 2 × n P=\bf 2\times n P=2×n, take C 1 = { ( 2 , j ) : j ∈ n } C_1=\{(2,j):\ j\in \bf n\} C1={ (2,j): j∈n}, C 2 = { ( 1 , j ) : j ∈ n } C_2=\{(1,j):\ j\in\bf n\} C2={ (1,j): j∈n}, be δ ( J ( P ) ) = { ( i , j ) ∈ N 2 : 0 ≤ i ≤ j ≤ n } \delta(J(P))=\{(i,j)\in\mathbb{N}^2:\ 0\leq i\leq j \leq n\} δ(J(P))={ (i,j)∈N2: 0≤i≤j≤n}. When n = 3 n=3 n=3, namely P = 2 × 3 P=\bf 2\times 3 P=2×3, Posets P P P As shown below :

Easy to get J ( P ) J(P) J(P) Here's the picture :

This is equivalent to not passing through y = x y=x y=x The number of lattice paths that only go up and right one lattice , Obviously, the picture shows 5 5 5. In a general way , e ( 2 × n ) = 1 n + 1 ( 2 n n ) e(2\times {\bf n})=\frac1{n+1}\binom {2n}n e(2×n)=n+11(n2n).
Recursive relations
take e e e regard as J ( P ) J(P) J(P) The function on , That is, if I ∈ J ( P ) I\in J(P) I∈J(P), be e ( I ) e(I) e(I) Express I I I As P P P The number of partially ordered subsets of the extension to totally ordered sets , therefore e ( I ) e(I) e(I) Equal to the J ( P ) J(P) J(P) In the from 0 ^ \hat0 0^ To I I I The number of saturated chains . therefore
e ( I ) = ∑ I ′ e ( I ′ ) , e(I)=\sum_{I'}e(I'), e(I)=I′∑e(I′),
among I ′ I' I′ Take over J ( P ) J(P) J(P) in I I I All elements covered , Similar to Yanghui triangle , e ( I ) e(I) e(I) It happens to be I I I Below e ( I ′ ) e(I') e(I′) And .
A simple example is P = N + N P=\mathbb{N+N} P=N+N, remember J f ( P ) J_f(P) Jf(P) by P P P Lattice of finite ordered ideals of , Then there are J f ( P ) ≅ N × N J_f(P)\cong \mathbb{N\times N} Jf(P)≅N×N.

边栏推荐
- DBMS in Oracle_ output. put_ Example of line usage
- 《被讨厌的勇气》读后感
- RobotFramework 安装教程
- Interview MySQL
- Thread pool: reading the source code of threadpoolexcutor
- std::enable_ shared_ from_ This error: error: expected template name before '<' token
- Preliminary controller input of oculus learning notes (1)
- Plan and change of continuous repair
- Complete the sqlsession interface and implementation classes
- How MySQL deletes a column in a database table
猜你喜欢
随机推荐
The Fourth Youth Life Science Forum | first round notice
每天5分钟玩转Kubernetes | Dashboard典型使用场景
Makefile does not compile some files
Method of activity jump to fragment (intent)
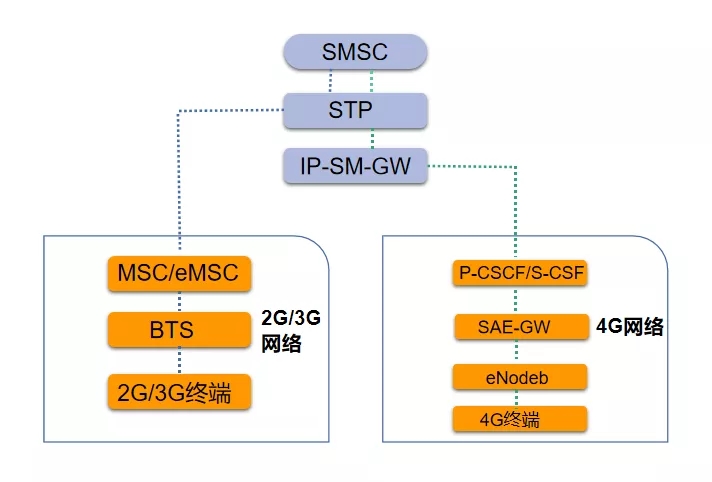
5g short message solution
自定义数据库连接池类: 要求:封闭一个Collection对象的集合类
Chrome suddenly can't copy and paste
JVM quick start
助力客户数字化转型,构建全新的运维体系
AIOps 智能运维经验分享
STM32控制矩阵按键,HAL库,cubeMX配置
Redis中的布隆过滤器与布谷鸟过滤器,你了解多少?
贪心之区间问题(4)
牛客网:最小覆盖子串
Redis usage scenario sharing (project practice)
Interview MySQL
静态链表(一)
Iplook, as a member of o-ran alliance, will jointly promote the development of 5g industry
Traditional image -- LBP feature
org.apache.ibatis.binding.BindingException: Invalid bound statement (not found)