当前位置:网站首页>689. 三个无重叠子数组的最大和
689. 三个无重叠子数组的最大和
2022-08-03 23:01:00 【小卢要刷力扣题】
前言
给你一个整数数组 nums 和一个整数 k ,找出三个长度为 k 、互不重叠、且全部数字和(3 * k 项)最大的子数组,并返回这三个子数组。
以下标的数组形式返回结果,数组中的每一项分别指示每个子数组的起始位置(下标从 0 开始)。如果有多个结果,返回字典序最小的一个。
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/maximum-sum-of-3-non-overlapping-subarrays
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
一、解题思路
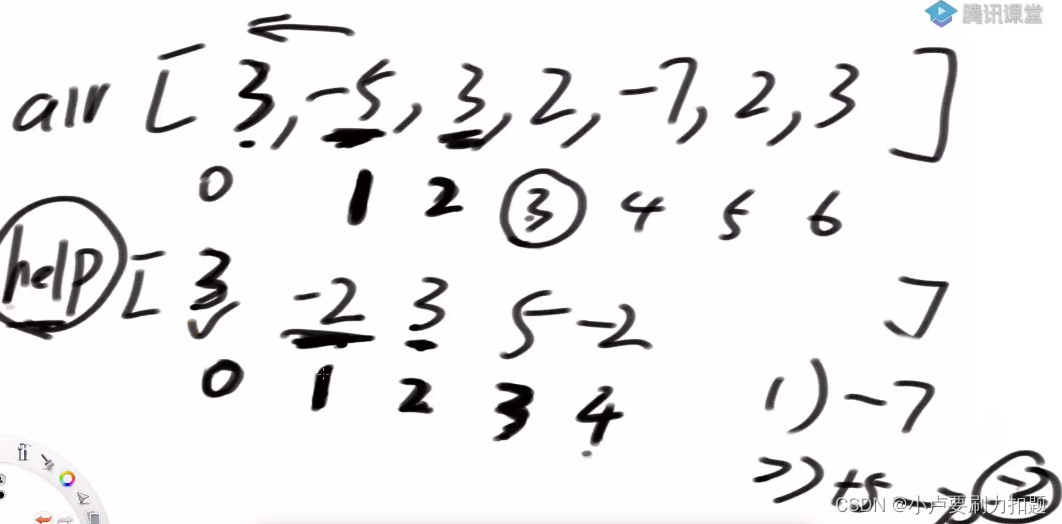
help数组
help[1]:子数组必须以1位置数结尾情况下,累加和怎么最好
第一种可能性:只包含-5
第二种可能性: -5决定往左扩
help的含义是子数组必须以0位置的数结尾的情况下最好收益是啥?
子数组必须以1位置的数结尾的情况下最好收益是啥?
子数组必须以2位置的数结尾的情况下最好收益是啥?
…
然后利用help数组求dp数组
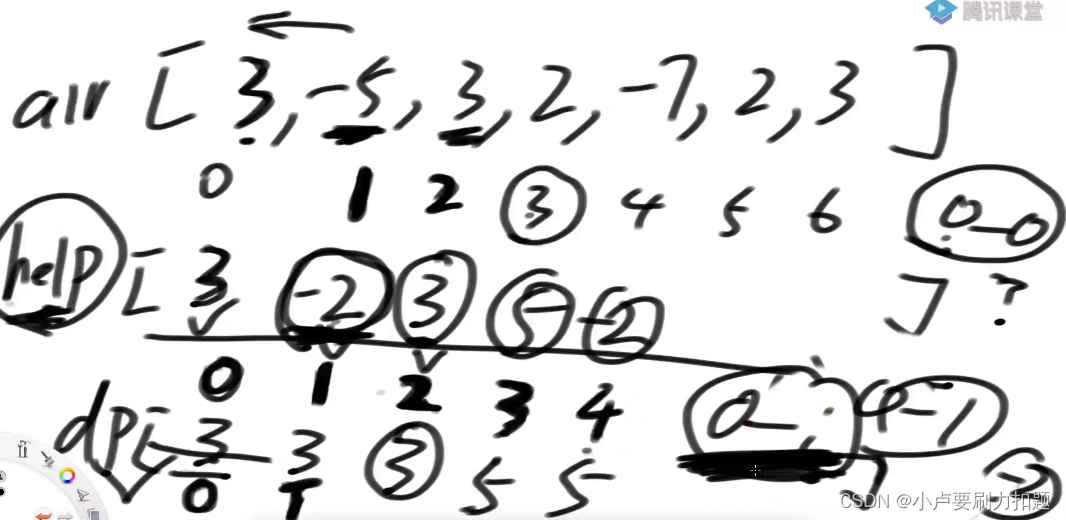
dp数组
dp[0]: 0~0范围上随意选,累加和怎么最好
dp[1]:
子数组必须以1结尾,最好收益是-2
子数组不以1位置结尾情况下怎么最好,就是之前的答案3
两种可能性求最大值
dp[i]: 0~i范围上随意选,子数组的累加和怎么最好
public static int maxSumLenK(int[] arr, int k) {
int N = arr.length;
// 子数组必须以i位置的数结尾,长度一定要是K,累加和最大是多少?
// help[0] help[k-2] ...
int sum = 0;
for (int i = 0; i < k - 1; i++) {
sum += arr[i];
}
// 0...k-2 k-1 sum
int[] help = new int[N];
for (int i = k - 1; i < N; i++) {
// 0..k-2
// 01..k-1
sum += arr[i];
help[i] = sum;
// i == k-1
sum -= arr[i - k + 1];
}
// help[i] - > dp[i] 0-..i K
}
原问题题解
原问题:必须选3个非空子数组,长度一定是K, 无重合,累加和最大.
整个数组从左往右遍历生成dp数组
再从右往左生成dp数组: i~N-1范围上,如果只选一个子数组… 累加和怎么最大
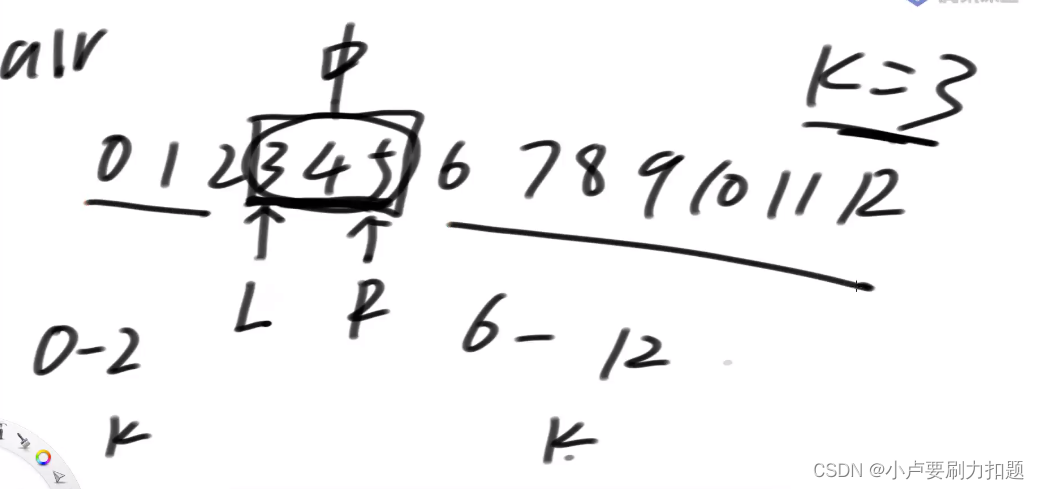
让L到R的距离为K,L…R是中间的子数组,k=3
问题变为中间数组必须是3~ 5的话,0~ 2范围和6~12范围上怎么选一个子数组最好,
左右两边的信息直接查表可以得到
第一回, L来到3, R来到5,我们查0~ 2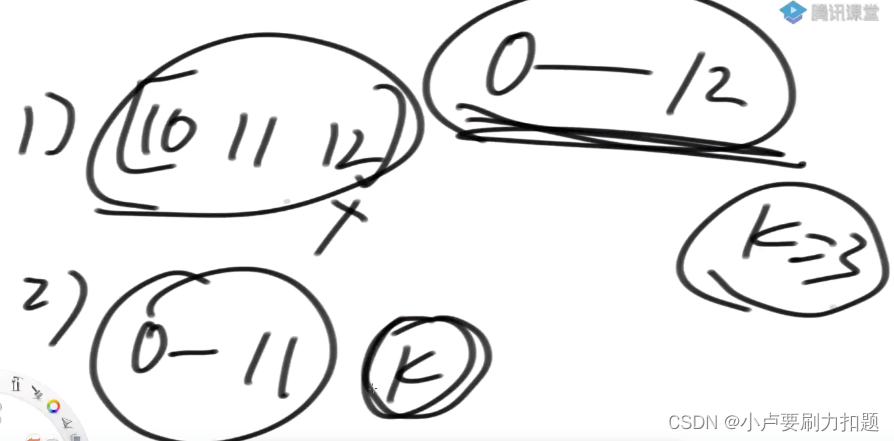
0-12范围上K-定是长度为3的数组,有那些可能性
1)就是10.11,12三个数组成的子数组.
2)子数组不以12结尾就是0-11范围上选K个在0~12范围上
就怎么选K个
代码
class Solution {
public int[] maxSumOfThreeSubarrays(int[] nums, int k) {
int n=nums.length;
int[] range=new int[n];
int[] left=new int[n];
int sum=0;
for(int i=0;i<k;i++){
sum+=nums[i];
}
range[0]=sum;
left[k-1]=0;
int max=sum;
for(int i=k;i<n;i++){
sum = sum - nums[i - k] + nums[i];
range[i - k + 1] = sum;
left[i] = left[i - 1];
if (sum > max) {
max = sum;
left[i] = i - k + 1;
}
}
sum=0;
for(int i=n-1;i>=n-k;i--){
sum+=nums[i];
}
max=sum;
int[] right=new int[n];
right[n-k]=n-k;
for(int i=n-k-1;i>=0;i--){
sum=sum-nums[i+k]+nums[i];
right[i]=right[i+1];
if(sum>=max){
max=sum;
right[i]=i
; }
}
int a=0;
int b=0;
int c=0;
max=0;
for(int i=k;i<n-2*k+1;i++){
int part1=range[left[i-1]];
int part2=range[i];
int part3=range[right[i+k]];
if(part1+part2+part3>max){
max = part1 + part2 + part3;
a = left[i - 1];
b = i;
c = right[i + k];
}
}
return new int[] {
a, b, c };
}
}
边栏推荐
- 重发布实验报告
- 【day1】
- 一个函数有多少种调用方式?
- 伴随着元宇宙、web3.0等概念的兴起,数字人、数字场景等诸多数字化的形态开始出现
- Analysys Analysis: The transaction scale of China's online retail B2C market in Q2 2022 will reach 2,344.47 billion yuan
- LabVIEW code generation error 61056
- Live Preview | Build Business Intelligence, Quickly Embrace Financial Digital Transformation
- Zilliz 2023 Fall Campus Recruitment Officially Launched!
- BMN: Boundary-Matching Network for Temporal Action Proposal Generation阅读笔记
- 如何创建一个Web项目
猜你喜欢

AOSP CameraLatencyHistogram的原理与使用
如何创建一个Web项目

FinClip最易用的智能电视小程序

软测人每个阶段的薪资待遇,快来康康你能拿多少?
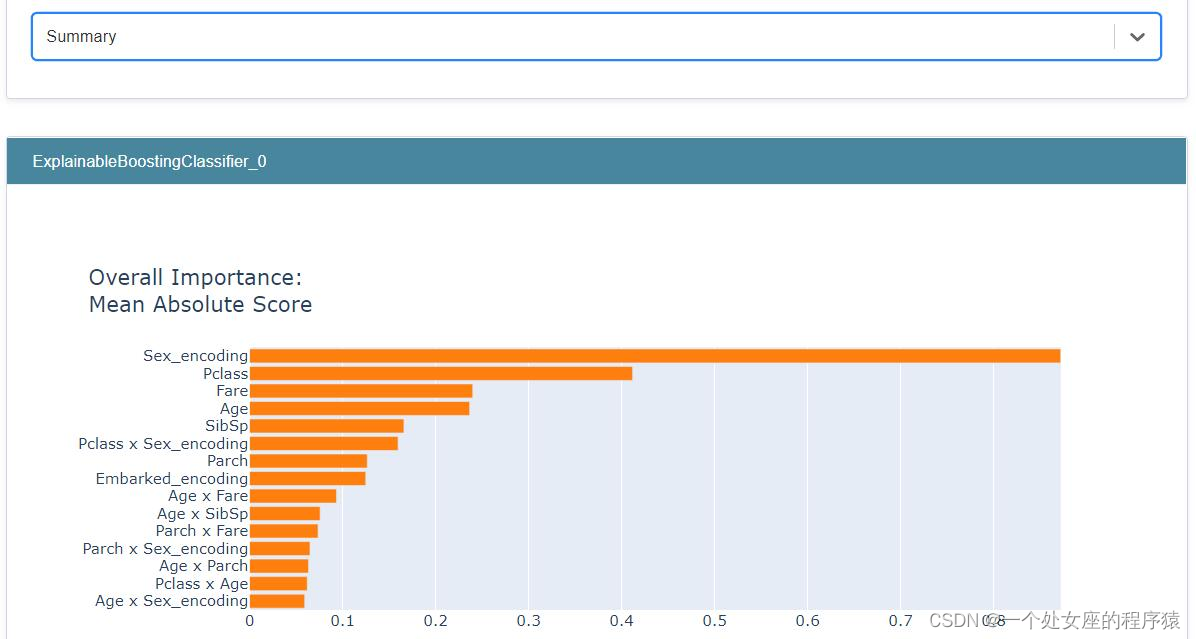
Interpretation of ML: A case of global interpretation/local interpretation of EBC model interpretability based on titanic titanic rescued binary prediction data set using interpret

SPOJ 2774 Longest Common Substring(两串求公共子串 SAM)
用栈实现队列

Cloud platform construction solutions
【day6】类与对象、封装、构造方法
图论-虚拟节点分层建图
随机推荐
雅思大作文写作模版
Unity2021 releases WebGL fog effect disappearing problem
"Digital Economy Panorama White Paper" Financial Digital User Chapter released!
2022-08-03 Oracle executes slow SQL-Q17 comparison
用队列模拟实现栈
utils 定时器
响应式织梦模板除尘器类网站
Zilliz 2023 秋季校园招聘正式启动!
V8中的快慢数组(附源码、图文更易理解)
工作小计 QT打包
软件测试内卷严重,如何提升自己的竞争力呢?
Create function report error, prompting DECLARE definition syntax problem
Boss: There are too many systems in the company, can you realize account interoperability?
[RYU] rest_router.py source code analysis
Research status of target detection at home and abroad
P1996 约瑟夫问题
响应式织梦模板餐饮酒店类网站
[N1CTF 2018] eating_cms
Creo 9.0在草图环境中创建坐标系
P1449 后缀表达式