当前位置:网站首页>【Leetcode】416. Split equal sum subset
【Leetcode】416. Split equal sum subset
2022-06-12 11:59:00 【Greenary】
Topic link : To divide into equal and subsets
Title Description : To give you one Contains only positive integers Of Non empty Array nums . Please decide whether you can divide this array into two subsets , Make the sum of the elements of the two subsets equal .
Ideas : Split the array into two equal sum subsets .
that :
1) The sum of array elements must be even , And the array length must be greater than 1. And the maximum value of the array cannot be greater than half of the sum of the array
2) The question turned to : Whether there are several elements in the array , The sum is half the sum of all the elements of the array . That is to find the sum of several elements as target.
The original idea is : Sort elements , Then use the method of backtracking , Passed 100 Multiple samples . A few sample errors remain , After repeated thinking and trying to find the method of backtracking is not right .
So I read the solution , See light suddenly .
0-1 knapsack problem :
Yes n Two objects and a backpack , take n Several of the objects are put into the backpack . Each object can only be placed 1 Time , That is to say, every object is either placed or , Or not .
The corresponding question is ,n Select several of the objects and put them into one with the size of target The backpack , Can it be just full .
Define an array dp[n][target+1],dp[i][j] Indicates whether or not [0,i] Select several of the numbers so that the sum is just j. Final dp[n-1][target] It's what you want . Adopted Dynamic programming Thought .
Because every object can be put or not , So there is a classified discussion , The state transition equation is obtained .
If j==nums[i], Then only the i One object is enough , namely dp[i][j]=true,
If j<nums[i], Is the first i Objects cannot be placed in a size of j In my backpack , Only in the past [0,i-1] Take from objects , namely dp[i][j]=dp[i-1][j].
If j>nums[i], So the first i Objects can be placed in a size of j In my backpack , You can also choose not to put . namely dp[i][j]=dp[i-1][j] || dp[i-1][j-nums[i]]
The boundary condition is : The first column is full of false, The first line is just nums[0] The corresponding value is true.
js The code is as follows :
var canPartition = function (nums) {
const length = nums.length;
if (length == 1)
return false;
let sum = 0;
let max=0;
for (let num of nums) {
sum += num;
max=Math.max(max,num);
}
const target=sum/2;
if (sum % 2 == 1)
return false;
if(max>target)
return false;
let dp=new Array(length);
for(let i=0;i<length;i++){
dp[i]=new Array(target+1).fill(false);
}
dp[0][nums[0]]=true;
for(let i=1;i<length;i++){
for(let j=1;j<=target;j++){
if(j===nums[i])
dp[i][j]=true;
else if(j<nums[i])
dp[i][j]=dp[i-1][j];
else
dp[i][j]=dp[i-1][j] || dp[i-1][j-nums[i]];
}
}
return dp[length-1][target];
};
Time complexity :O(n target), Spatial complexity O(n target)
From the state transfer equation we can see that ,dp Each row of the is only related to data of the previous row , So there is no need to maintain a two-dimensional array , You can use one-dimensional arrays .
namely dp[j]=dp[j] || dp[j-nums[i]], here dp[j] and dp[j-nums[i]] It should be the data before updating , So in the j When traversing , It should be from the back to the front , This ensures that dp[j-nums[i]] It has not been updated . If from the past to the future , Then we will use dp[j-nums[i]] It's the updated , Cause the result to go wrong . If you traverse from front to back , Also can put the dp[j-nums[i]] Put it in storage .
js The code is as follows :
var canPartition = function (nums) {
const length = nums.length;
if (length == 1)
return false;
let sum = 0;
let max = 0;
for (let num of nums) {
sum += num;
max = Math.max(max, num);
}
const target = sum / 2;
if (sum % 2 == 1)
return false;
if (max > target)
return false;
// One dimensional arrays can also
let dp = new Array(target + 1).fill(false);
dp[nums[0]] = true;
dp[0] = true;
for (let i = 1; i < length; i++) {
// debugger
for (let j = target; j >= nums[i]; j--) {
dp[j] = dp[j] || dp[j - nums[i]];
}
}
return dp[target];
};Time complexity :O(n target), Spatial complexity O(target)
边栏推荐
- ARM指令集之Load/Store指令寻址方式(一)
- Decision tree of machine learning
- Basic concepts of machine learning
- IP地址管理
- 视频分类的类间和类内关系——正则化
- TinyMCE series (I) TinyMCE environment construction
- UML series articles (30) architecture modeling -- product diagram
- Must do skill -- use ffmpeg command to quickly and accurately cut video
- Rich text editor copying pictures in word documents
- ARM指令集之数据处理类指令
猜你喜欢

UML series articles (31) architecture modeling - deployment diagram

寻找两个有序数组的中位数(LeetCode 4)

LeetCode 1037. Effective boomerang (vector cross product)
![[foundation of deep learning] learning of neural network (4)](/img/8d/0e1b5d449afa583a52857b9ec7af40.png)
[foundation of deep learning] learning of neural network (4)

必杀技--使用FFmpeg命令快速精准剪切视频

Chaîne la plus longue sans caractères dupliqués (leetcode 3)

A. Prefix range
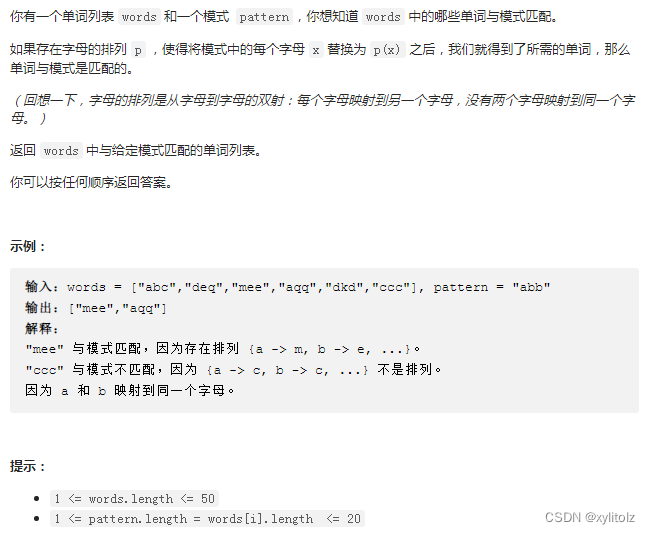
LeetCode 890. Find and replace mode (analog + double hash table)

TinyMCE series (I) TinyMCE environment construction

5G NR協議學習--TS38.211下行通道
随机推荐
LeetCode 497. Random points in non overlapping rectangles (prefix and + bisection)
TinyMCE series (III) introduction to common TinyMCE APIs
视频分类的类间和类内关系——正则化
Data processing instruction addressing method of arm instruction set
Deep learning and CV tutorial (14) | image segmentation (FCN, segnet, u-net, pspnet, deeplab, refinenet)
ARM处理器模式与寄存器
Tpage design
LeetCode_字符串_简单_344.反转字符串
树的前序,中序,后序遍历
Load/store memory access instruction of arm instruction set (1)
Compiling Draco library on Windows platform
Decision tree of machine learning
用cloneNode 克隆,解决id问题/方法 深复制和浅复制修改id的方法
Unit test case framework --unittest
SSL引入原因及加密步骤
异步路径处理
Channel Shuffle类
[foundation of deep learning] back propagation method (1)
Reprint --win10 open the task manager to solve the blue screen problem
Data processing instructions of arm instruction set