当前位置:网站首页>LeetCode952三部曲之一:解题思路和初级解法(137ms,超39%)
LeetCode952三部曲之一:解题思路和初级解法(137ms,超39%)
2022-08-01 21:33:00 【程序员欣宸】
欢迎访问我的GitHub
这里分类和汇总了欣宸的全部原创(含配套源码):https://github.com/zq2599/blog_demos
题目描述
- 难度:困难
- 编程语言:Java
- 给定一个由不同正整数的组成的非空数组 nums ,考虑下面的图:
- 有 nums.length 个节点,按从 nums[0] 到 nums[nums.length - 1] 标记;
- 只有当 nums[i] 和 nums[j] 共用一个大于 1 的公因数时,nums[i] 和 nums[j]之间才有一条边。
- 返回图中最大连通组件的大小
- 示例 1:

输入:nums = [4,6,15,35]
输出:4
- 示例 2:

输入:nums = [20,50,9,63]
输出:2
- 示例 3:

输入:nums = [2,3,6,7,4,12,21,39]
输出:8
- 提示:
- 1 <= nums.length <= 2 * 104
- 1 <= nums[i] <= 105
- nums 中所有值都 不同
审题
- 可能是自身天资愚钝,欣宸第一时间居然没有搞懂题目中连通组件的大小的含义,以示例一为例,如下图,明明是三个边,为啥答案是4?

- 好吧,晕晕乎乎的想了半天终于搞清楚了:
- 不是让你数有几条边!
- 是让你数能够连在一起的元素,最多有几个?
- 如下图,有四个连在一起,答案就是4

- 如下图,50和9之间没有公因数,所以连不起来,导致四个数字中,20和50相连,9和63相连,那么,能连在一起的两个组合中,每个组合的数量都是2,答案就是2

- 磕磕绊绊终于读懂了题,再来看看解题前对知识储备的要求
需要哪些基本功?
- 请先掌握下面两个基本功,然后再能愉快的解题和优化,享受AC的喜悦,以及超过人数百分比提升的成就感
- 计算素数(埃氏筛选或者欧拉筛选,我这里用的是欧拉筛选)
- 并查集,需掌握以下技术点:
- 数据结构是数组,下标代表数字,值代表父节点是谁
- 查找(查找时顺便优化路径)
- 合并
- 上述基本功相信难不倒聪明的您,半小时内就能掌握,接下来,在欣宸图文并茂的解说中,一起享受解hard题的快乐吧
题目中还有哪些重要信息?
- 除了基本命题,还有三个至关重要的信息需要重点关注,他们是解题的关键,如下图,请记住这三个信息,很快就会用到

- 至此,准备工作已经完成,可以开始分析解题思路了,图文并茂的分析中,可能会让您产生一个错觉:hard题,就这?
解题思路
- 先画个图来描述完整流程

- 上面这个图,一开始可能您会看得有点晕乎,HashMap到底存了啥?并查集合并又合并了啥?
- 看不明白没事,真的没事,此图其实是解题思路的提前小结,接下来咱们用实际数字来演示解题思路,总之,就是要以最简单和具体的手段让您理解思路
实例解题演示解题思路
- 注意,接下来还是分析思路,暂时不涉及代码
- 以官方的示例来演示解题过程吧,假设输入数组有四个数字:4、6、15、35
- 首先,计算出每个数字的质因数,如下图,4的质因数是2,6的质因数是2和3,应该很好理解

- 接下来,根据上面的计算结果,新建一个HashMap,key是质因数,value是原数字,以2为例,它是4和6的质因数,所以,key就是2,value是个ArrayList,里面的内容是4和6,也就是说,根据上面的图得出下面的图

- 现在新建一个并查集,由于数字大小范围是从1到100000,所以,为了用数组下标表示数字,组数的大小就是100001,如此一来,array[100000]=123的意思就是:100000这个数字的父节点是123,这就是并查集概念中的数组定义的标准含义了
- 注意,数组创建后,每个元素值都是0,如下图
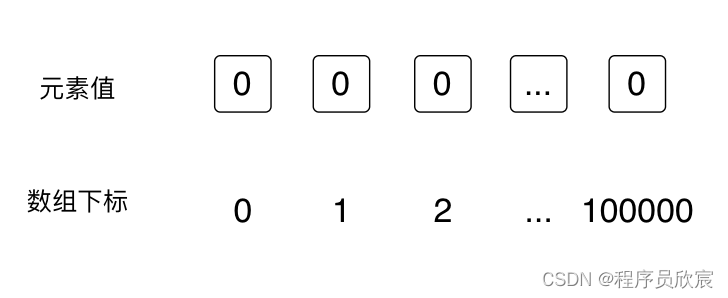
- 在本题中,咱们只关心4、6、15、35这四个数字,所以接下来画图的时候,数组中其他数字就不画上去了,后面的分析中,数组画出来就是下图的效果,相信您可以理解

- 按照并查集的定义,最初的时候,每个元素的父节点是它自己,所以给数组中每个元素赋值,值就等于数组下标,如下图所示,注意下图新增了辅助理解的逻辑图,这个是用来帮助大家理解每个节点和父节点关系的,可以看到每个节点的箭头指向自己,表示自己是自己的父节点(或者说每个元素都是根节点)

- 接下来,遍历前面准备好的HashMap,每个key对应的都是一个List,将这个list中的所有元素在并查集中合并,以key等于2为例,value中有两个数字:4和6,所以,在并查集中将4和6合并
- 第一个key是2,value中的数字是4和6,将4和6合并的效果如下图,红色是改过的地方,值等于4,表示数字6的父节点改成了4,为了便于理解,逻辑图也同步改动了,6指向自己的父节点4

- 第二个key是3,value中的数字是6和15,将6和15合并的效果如下图,蓝色是改过的地方,值等于6,表示数字15的父节点改成了6,为了便于理解,逻辑图也同步改动了,15指向自己的父节点6(逻辑图上可见,尽管只改了15的父节点,然而4,6,15已经在同一个树下了)

- 第三个key是5,value中的数字是15和35,将15和15合并的效果如下图,绿色是改过的地方,值等于15,表示数字35的父节点改成了15,为了便于理解,逻辑图也同步改动了,35指向自己的父节点15

- 至于第四个key,即7,它的value中只有一个数字35,谈不上合并,所以不做任何操作
- 至此,并查集合并操作完成,纵观整个并查树,虽然有多个树,唯有以4为根节点的树,其元素最多,有四个,所以,此题返回值就是4,连通的四个元素是4-6-15-35
- 画图画到手抽筋,相信您对解题思路已经完全掌握,接下来,开始编码吧
编码
- 接下来的编码,先将几个关键点逐个列举,然后再给出完整代码,并且会附上详细的注解,相信您可以轻松读懂
- 首先看看要定义哪些成员变量,如下,map是最重要的,刚才咱们详细分析过,代码注解也说得很细致了,然后是fathers、rootSetSize、maxRootSetSize都是并查集相关的数据结构
// 并查集的数组, fathers[3]=1的意思是:数字3的父节点是1
int[] fathers = new int[100001];
// 并查集中,每个数字与其子节点的元素数量总和,rootSetSize[5]=10的意思是:数字5与其所有子节点加在一起,一共有10个元素
int[] rootSetSize = new int[100001];
// map的key是质因数,value是以此key作为质因数的数字
// 例如题目的数组是[4,6,15,35],对应的map就有四个key:2,3,5,7
// key等于2时,value是[4,6],因为4和6的质因数都有2
// key等于3时,value是[6,15],因为6和16的质因数都有3
// key等于5时,value是[15,35],因为15和35的质因数都有5
// key等于7时,value是[35],因为35的质因数有7
Map<Integer, List<Integer>> map = new HashMap<>();
// 用来保存并查集中,最大树的元素数量
int maxRootSetSize = 1;
- 并查集的查找根节点的操作也要注意,在查找过程中,将每个元素的父节点都改成了根节点,这就是常规的压缩操作
/** * 带压缩的并查集查找(即寻找指定数字的根节点) * @param i */
private int find(int i) {
// 如果执向的是自己,那就是根节点了
if(fathers[i]==i) {
return i;
}
// 用递归的方式寻找,并且将整个路径上所有长辈节点的父节点都改成根节点,
// 例如1的父节点是2,2的父节点是3,3的父节点是4,4就是根节点,在这次查找后,1的父节点变成了4,2的父节点也变成了4,3的父节点还是4
fathers[i] = find(fathers[i]);
return fathers[i];
}
- 并查集的合并操作也有个细节要注意,每次合并后,根节点下属元素会增加,将总数统一出来,再和maxRootSetSize比较一下,这样持续的操作后,maxRootSetSize记录的就是最大的树的元素个数
/** * 并查集合并,合并后,child会成为parent的子节点 * @param parent * @param child */
private void union(int parent, int child) {
int parentRoot = find(parent);
int childRoot = find(child);
// 如果有共同根节点,就提前返回
if (parentRoot==childRoot) {
return;
}
// child元素根节点是childRoot,现在将childRoot的父节点从它自己改成了parentRoot,
// 这就相当于child所在的整棵树都拿给parent的根节点做子树了
fathers[childRoot] = fathers[parentRoot];
// 合并后,这个树变大了,新增元素的数量等于被合并的字数元素数量
rootSetSize[parentRoot] += rootSetSize[childRoot];
// 更像最大数量
maxRootSetSize = Math.max(maxRootSetSize, rootSetSize[parentRoot]);
}
- 在来看一下得到数字的质因数的操作,如下所示:
// 对数组中的每个数,算出所有质因数,构建map
for (int i=0;i<nums.length;i++) {
int cur = nums[i];
for (int j=2;j*j<=cur;j++) {
// 从2开始逐个增加,能整除的一定是质数
if(cur%j==0) {
map.computeIfAbsent(j, key -> new ArrayList<>()).add(nums[i]);
}
// 从cur中将j的因数全部去掉
while (cur%j==0) {
cur /= j;
}
}
// 能走到这里,cur一定是个质数,
// 因为nums[i]被除过多次后结果是cur,所以nums[i]能被cur整除,所以cur是nums[i]的质因数,应该放入map中
if (cur!=1) {
map.computeIfAbsent(cur, key -> new ArrayList<>()).add(nums[i]);
}
}
- 关键代码已经看完了,来看看完整版代码
class Solution {
// 并查集的数组, fathers[3]=1的意思是:数字3的父节点是1
int[] fathers = new int[100001];
// 并查集中,每个数字与其子节点的元素数量总和,rootSetSize[5]=10的意思是:数字5与其所有子节点加在一起,一共有10个元素
int[] rootSetSize = new int[100001];
// map的key是质因数,value是以此key作为质因数的数字
// 例如题目的数组是[4,6,15,35],对应的map就有四个key:2,3,5,7
// key等于2时,value是[4,6],因为4和6的质因数都有2
// key等于3时,value是[6,15],因为6和16的质因数都有3
// key等于5时,value是[15,35],因为15和35的质因数都有5
// key等于7时,value是[35],因为35的质因数有7
Map<Integer, List<Integer>> map = new HashMap<>();
// 用来保存并查集中,最大树的元素数量
int maxRootSetSize = 1;
/** * 带压缩的并查集查找(即寻找指定数字的根节点) * @param i */
private int find(int i) {
// 如果执向的是自己,那就是根节点了
if(fathers[i]==i) {
return i;
}
// 用递归的方式寻找,并且将整个路径上所有长辈节点的父节点都改成根节点,
// 例如1的父节点是2,2的父节点是3,3的父节点是4,4就是根节点,在这次查找后,1的父节点变成了4,2的父节点也变成了4,3的父节点还是4
fathers[i] = find(fathers[i]);
return fathers[i];
}
/** * 并查集合并,合并后,child会成为parent的子节点 * @param parent * @param child */
private void union(int parent, int child) {
int parentRoot = find(parent);
int childRoot = find(child);
// 如果有共同根节点,就提前返回
if (parentRoot==childRoot) {
return;
}
// child元素根节点是childRoot,现在将childRoot的父节点从它自己改成了parentRoot,
// 这就相当于child所在的整棵树都拿给parent的根节点做子树了
fathers[childRoot] = fathers[parentRoot];
// 合并后,这个树变大了,新增元素的数量等于被合并的字数元素数量
rootSetSize[parentRoot] += rootSetSize[childRoot];
// 更像最大数量
maxRootSetSize = Math.max(maxRootSetSize, rootSetSize[parentRoot]);
}
public int largestComponentSize(int[] nums) {
// 对数组中的每个数,算出所有质因数,构建map
for (int i=0;i<nums.length;i++) {
int cur = nums[i];
for (int j=2;j*j<=cur;j++) {
// 从2开始逐个增加,能整除的一定是质数
if(cur%j==0) {
map.computeIfAbsent(j, key -> new ArrayList<>()).add(nums[i]);
}
// 从cur中将j的因数全部去掉
while (cur%j==0) {
cur /= j;
}
}
// 能走到这里,cur一定是个质数,
// 因为nums[i]被除过多次后结果是cur,所以nums[i]能被cur整除,所以cur是nums[i]的质因数,应该放入map中
if (cur!=1) {
map.computeIfAbsent(cur, key -> new ArrayList<>()).add(nums[i]);
}
}
// 至此,map已经准备好了,接下来是并查集的事情,先要初始化数组
for(int i=0;i< fathers.length;i++) {
// 这就表示:数字i的父节点是自己
fathers[i] = i;
// 这就表示:数字i加上其下所有子节点的数量等于1(因为每个节点父节点都是自己,所以每个节点都没有子节点)
rootSetSize[i] = 1;
}
// 遍历map
for (int key : map.keySet()) {
// 每个key都是一个质因数
// 每个value都是这个质因数对应的数字
List<Integer> list = map.get(key);
// 超过1个元素才有必要合并
if (null!=list && list.size()>1) {
// 取第0个元素作为父节点
int parent = list.get(0);
// 将其他节点全部作为地0个元素的子节点
for(int i=1;i<list.size();i++) {
union(parent, list.get(i));
}
}
}
return maxRootSetSize;
}
}
- 在LeetCode上提交,结果如下图,137ms,超过39.55%的用户

- 至此,初步尝试已经通过,尽管耗时偏高,39%的比例也过于勉强,但证明本题的解题思路是走得通的
- 本文接下来的篇幅,是对自己在解题过程中犯错的复盘,放在这里供您参考,如果您也有类似困惑,希望接下来的内容可以帮助到您
何为连通?
- 通过因数2可将 4, 6, 12连通,这句话啥意思?在看LeetCode高手们的解题过程时,常常看到他们提到连通,最初我是很难理解这个概念
- 这句话的意思是,因为4,6,12有共同的因数2,所以,4和6可以连线,4和12也可以连线,6和12也可以连线,简单的说就是有共同因素的数字,它们是可以随意连接的!
最大的误解
个人在做这道题的时候,最大的误解就是对并查集合并的理解错误,导致做错,这里列出来,以避免您犯相同错误
以4,6,15,35这四个数字为例,以2为质因数的有4和6,以3为质因数的有6和15,以5为质因数的有15和35,以7为质因数的有35,逻辑关系如下图

所以,我们在说并查集合并操作,到底在合并什么?(这是核心,理解正确,这道题就解开了)
之前的误解如下图,以为是将红色箭头指向的四个集合合并,这样就达到了连通效果,实际上这样的理解是大错特错

接下来是自我救赎的纠正之路
首先,图就是错误的,既然是并查集,就应该按照并查集的数据结构来画图:一个int数组,数组下标就代表具体数字,值代表该数字的父节点是谁,例如 a[2]=5,其含义就是数字2的父节点是5,这是基本定义
并查集初始化的时候,每个元素的父节点都是它自己,如下图,注意,这个数组的长度其实是36(既从0到35),但是其他元素都用不上,所以我们无需关注它们,也就没有画进图中

接下来就是本题最核心的操作:合并,究竟该怎么合并呢?
答案是:相同质因数的数字合并,也就是说:以2为质因数的是4和6,所以4和6合并,以3为质因数的是6和15,所以6和15合并,以5为质因数的是15和35,所以15和35合并,7的质因数只有35,那就没法合并了
以上就是合并的操作,没错,就是这么简单:在并查集中对拥有相同质因数的数字进行合并
看到这里,您应该会疑惑:这样的合并,和连通有什么关系?和解题又有什么关系呢?
不急,咱能就用上面的数组,合并一下试试,稍后就会见证奇迹,也许能帮您找到豁然开朗的感觉
为了形象的理解,接下来我给数组再配上图,用来更形象的表达元素之间的父子关系,合并前的数组和关系图如下图,每个圆圈都有个箭头指向自己,表示每个元素的父节点是自己

接下来,合并4和6,这里的做法是把4作为6的父节点,所以,如下图,数组下标为4的元素值等于6,用逻辑图来表示,就是6的箭头指向4

接下来该合并6和15了,它们都有质因数3,这一步非常关键,因为我就是在这一步恍然大悟的,如下图,将6的父节点设置为4,再看逻辑关系图,明明只是在合并6和15,然而,4、6、15已经连通了!

恍然大悟:我们无需对各个质因数之间做什么,只要将每个质因数对应的数字合并即可,有的数字本来就属于多个质因数,所有跨质因数的连接都是因为这个特点而存在!
接下来是连接15和35,相信聪明的您也已经彻底领悟了,此时4个元素已经连通了

最后质因数7对应的数字只有35,一个数字就不需要合并操作了
敬请期待
- 至此,952的解题思路以及最初级的解法实战已经完成,这么多图和示例,相信聪明的您对解答此题已经胸有成竹,然而耗时过长,超39%实在是过于落后了,不能忍,所以,接下来的章节咱们一起来对此题做第一次优化,看看能不能有所提升
你不孤单,欣宸原创一路相伴
边栏推荐
- Get started with Grafana in 15 minutes
- 牛血清白蛋白刺槐豆胶壳聚糖缓释纳米微球/多西紫杉醇的纳米微球DTX-DHA-BSA-NPs
- shell specification and variables
- 二分法中等 LeetCode6133. 分组的最大数量
- Homework 8.1 Orphans and Zombies
- Graph adjacency matrix storage
- 基于php旅游网站管理系统获取(php毕业设计)
- 关于npm的那些事儿
- 365 days challenge LeetCode1000 questions - Day 046 Generate a string with odd number of each character + add two numbers + valid parentheses
- groupByKey和reduceBykey的区别
猜你喜欢

How to choose Visibility, Display, and Opacity when interacting or animating

树莓派的信息显示小屏幕,显示时间、IP地址、CPU信息、内存信息(c语言),四线的i2c通信,0.96寸oled屏幕
基于php影视资讯网站管理系统获取(php毕业设计)

包含吲哚菁绿的多聚体白蛋白纳米球/载马钱子碱纳米粒的牛血清白蛋白微球的制备

如何优雅的性能调优,分享一线大佬性能调优的心路历程
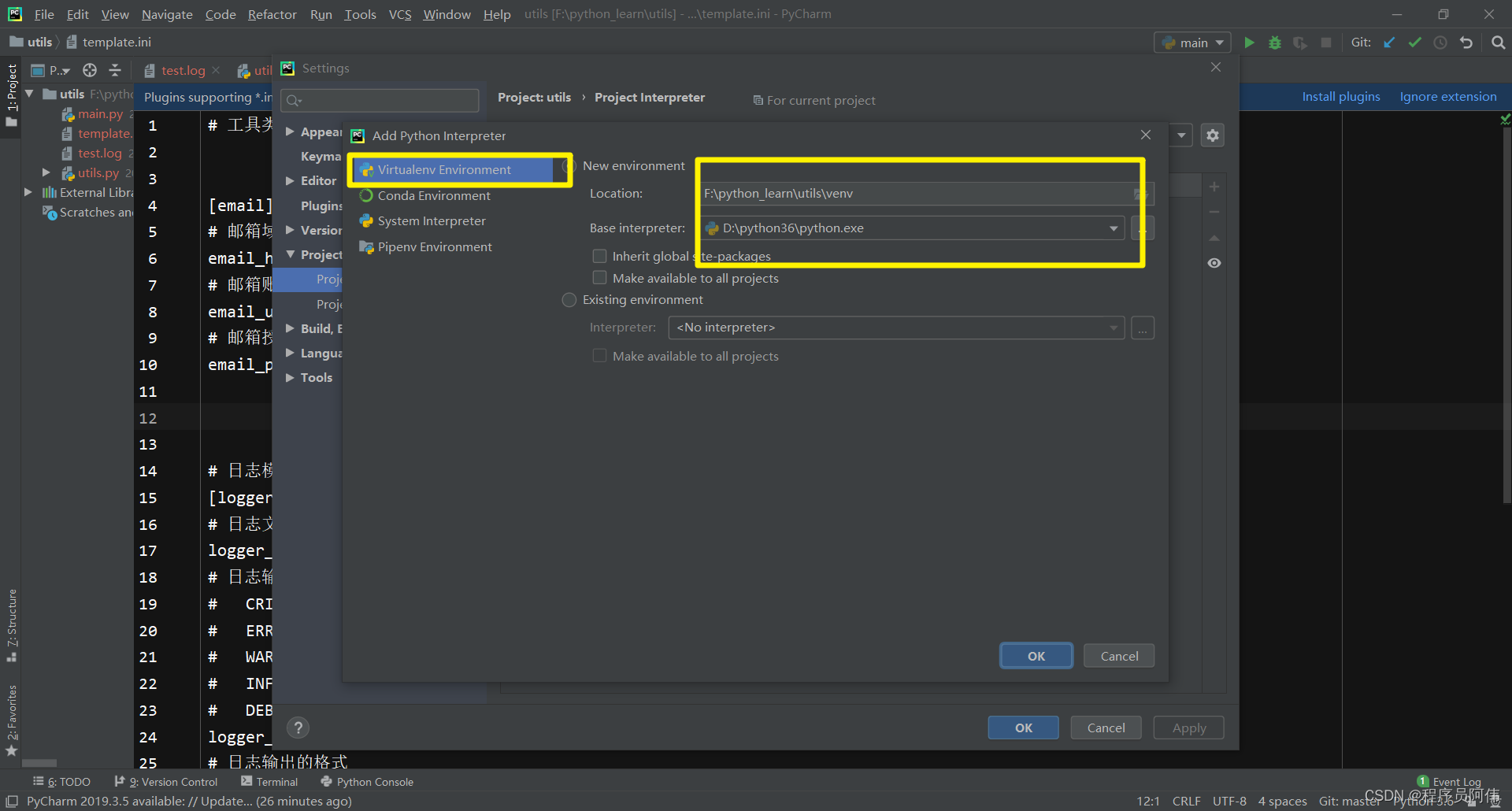
Anacoda的用途

Based on php film and television information website management system acquisition (php graduation design)

with语句和上下文管理器

RecycleView的使用
WEB 渗透之文件类操作
随机推荐
WEB 渗透之端口协议
基于php旅游网站管理系统获取(php毕业设计)
An online JVM FullGC made it impossible to sleep all night and completely crashed~
JS hoisting: how to break the chain of Promise calls
基于php在线考试管理系统获取(php毕业设计)
Scala练习题+答案
JSD - 2204 - Knife4j framework - processing - Day07 response results
Image fusion GANMcC study notes
二分法中等 LeetCode6133. 分组的最大数量
C语言_枚举类型介绍
Day016 类和对象
数字图像处理 第十二章——目标识别
多商户商城系统功能拆解19讲-平台端发票管理
Suggestions and answer 8.1 C traps and defect chapter 8
关于npm的那些事儿
[Chinese tree tags - CTB]
包含吲哚菁绿的多聚体白蛋白纳米球/载马钱子碱纳米粒的牛血清白蛋白微球的制备
宝塔应用使用心得
51.【结构体初始化的两种方法】
【Objective-C中的@synthesize】