【八大排序②】选择排序（选择排序，堆排序）

目录

 

一、选择排序

关于选择排序 

算法步骤：

代码实现 

【直接选择排序的特性总结】

 二、堆排序

堆排序算法的基本思想

 【直接选择排序的特性总结】

---

一、选择排序

关于选择排序 

选择排序是一种简单直观的排序算法，无论什么数据进去都是 O(n²) 的时间复杂度。所以用到它的时候，数据规模越小越好。唯一的好处可能就是不占用额外的内存空间。

算法步骤：

1. 首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置。
2. 再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。
3. 重复第二步，直到所有元素均排序完毕。

代码实现 

/**
     * 选择排序
     * @param array
     */
    public static void selectSort(int[]array){
        for(int i = 0;i < array.length-1 ;i++) {
            int minIndex = i;
            for (int j = i + 1; j < array.length; j++) {
                if (array[j] < array[minIndex]) {
                    minIndex = j;
                }
            }
            if (minIndex != i) {
                swap(array, minIndex, i);
            }
        }
    }

【直接选择排序的特性总结】

• 直接选择排序思考非常好理解，但是效率不是很好。实际中很少使用
• 时间复杂度：O(N^2)
• 空间复杂度：O(1)
• 稳定性：不稳定

 二、堆排序

  之前我们已经介绍过了大根堆、小根堆的概念，而堆排序就是利用堆（排升序建大根堆，降序建小堆）进行排序的方法。

堆排序算法的基本思想

将待排序的序列构造成一个大根堆。此时整个序列的最大值就是堆顶的根结点。将它移走（其实就是将其与堆数组的末尾元素交换，此时末尾元素就是最大值），然后将剩余的 n-1 个序列重新构造成一个堆，这样就会得到 n 个元素中的次大值。如此反复执行，便能得到一个有序序列了

 以上动图源自别处

下面我们再拆解一下每个步骤

如图，就是一个大根堆，90为最大值，将90与20（末尾元素）互换

 此时90就成了整个堆序列的最后一个元素

将20经过调整，使得除90以外的结点继续满足大根堆的定义（所有结点都大于其孩子）

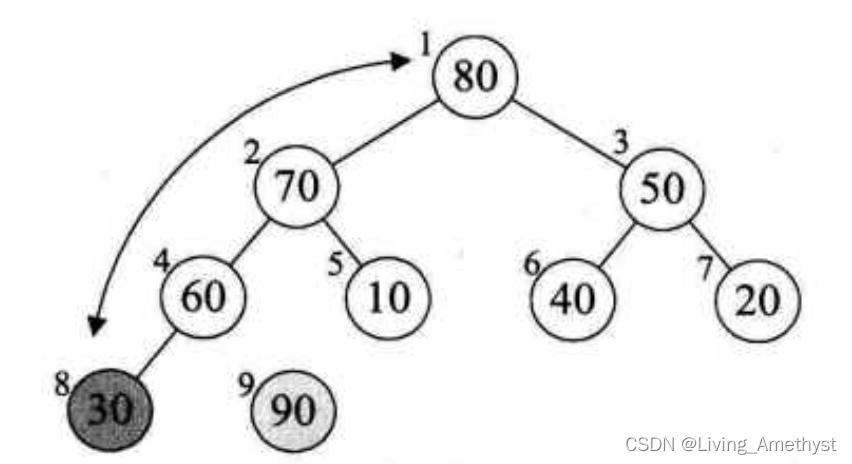
相信大家有些明白堆排序的基本思想了，但要完成堆排序，需要解决下面两个问题：

• 如何由一个无序序列构建成一个堆?
• 如果在输出堆顶元素后,调整剩余元素成为一个新的堆?

我们再看一张图体会一下（图源别处）

  

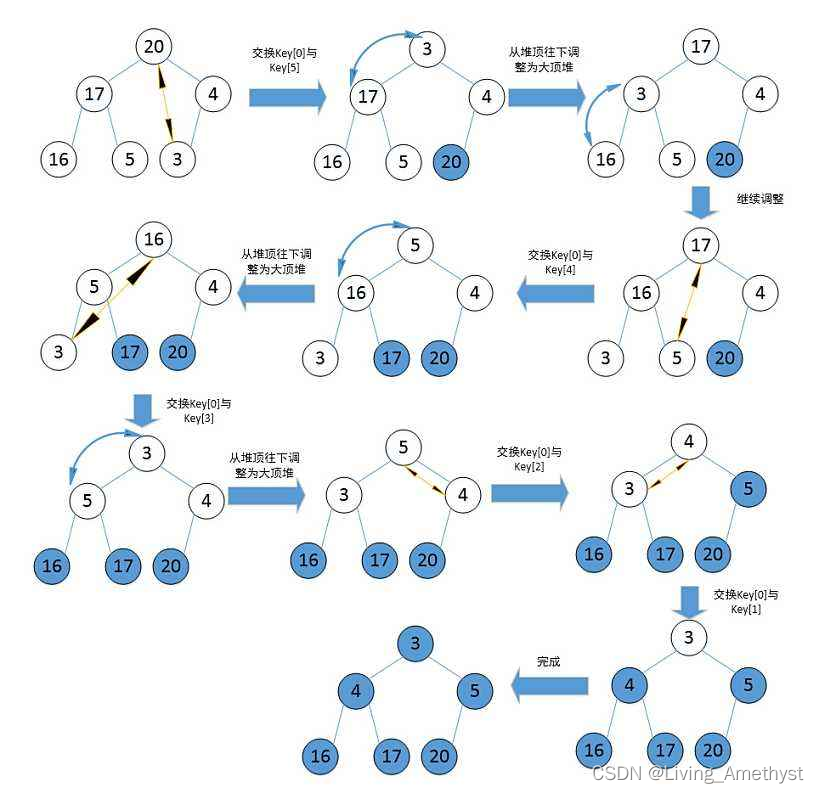
我们看代码

   /**
     * 堆排序
     * @param array
     * @param root
     * @param len
     */
    public static void shiftDown(int[]array,int root,int len){
        int parent = root;
        int child = (2*parent)+1;
        while(child < len) {
            if(child+1 < len  && array[child] < array[child + 1]) {
                child++;
            }
            if(array[child] > array[parent]){
                swap(array,child,parent);
                parent = child;
                child = (2*parent)+1;
            }else{
                break;
            }
        }
    }
    public static void createHeap(int[] array){
        for(int p = (array.length-1-1)/2; p>=0 ; p--){
            shiftDown(array,p, array.length);
        }
    }
    public static void heapSort(int[] array){
        createHeap(array);
        int end = array.length-1;
        while(end>=0){
            swap(array,0,end);
            shiftDown(array,0,end);
            end--;
        }
    }

 【直接选择排序的特性总结】

• 堆排序使用堆来选数，效率就高了很多。
• 时间复杂度：O(N*logN)
• 空间复杂度：O(1)
• 稳定性：不稳定