当前位置:网站首页>SDNU_ ACM_ ICPC_ 2022_ Weekly_ Practice_ 1st (supplementary question)
SDNU_ ACM_ ICPC_ 2022_ Weekly_ Practice_ 1st (supplementary question)
2022-06-11 22:50:00 【_ dawn°】
The first competition of school ! There are many original questions , But there are some things that haven't been dealt with during the winter vacation ,,,
B - Nuts

Each number in the calculation array is greater than 10 And .
Ideas : Traversal array addition , It won't explode int.
AC Code :
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define ios ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define INF 0x3f3f3f3f
// Determine whether it is necessary to open ll!!!
// Determine whether initialization is required !!!
const int mod=1e9+7;
const int N=1e3+5;
int n;
int a[N];
int ans;
int main()
{
// freopen("test.in","r",stdin);
// freopen("output.in", "w", stdout);
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i];
if(a[i]>10)
ans+=(a[i]-10);
}
cout<<ans<<'\n';
return 0;
}
D - Tour

give n Cities ,m One way road , How many pairs of city groups can serve as the starting point and the ending point .
Ideas : Chain forward star map ,DFS Search for each point .
AC Code :
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define ios ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define INF 0x3f3f3f3f
// Determine whether it is necessary to open ll!!!
// Determine whether initialization is required !!!
const int mod=1e9+7;
const int N=2e3+5;
int n,m;
int ver[N],nex[N],head[N],cnt;
bool vis[N];
void add_edge(int u,int v)
{
ver[++cnt]=v;
nex[cnt]=head[u];
head[u]=cnt;
}
void dfs(int x)
{
vis[x]=true;
for(int i=head[x];i;i=nex[i])
{
int y=ver[i];
if(vis[y]) continue;
dfs(y);
}
}
int main()
{
// freopen("test.in","r",stdin);
// freopen("output.in", "w", stdout);
cin>>n>>m;
for(int i=1;i<=m;i++)
{
int u,v;
cin>>u>>v;
add_edge(u,v);
}
int ans=0;
for(int i=1;i<=n;i++)
{
for(int i=1;i<=n;i++)
vis[i]=false;
dfs(i);
for(int i=1;i<=n;i++)
ans+=vis[i];
}
cout<<ans<<'\n';
return 0;
}
os:dfs Still not , A simple question took nearly two hours wwwwww, Practice more practice more
F - Rock-paper-scissors

The three men hammered their baggage into a draw , Give the choice of two of them , Ask the third person about their choice .
Ideas : If two people choose the same , Then the third person is the same ; If different , Then the third person chooses the remaining one .
AC Code :
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define ios ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define INF 0x3f3f3f3f
// Determine whether it is necessary to open ll!!!
// Determine whether initialization is required !!!
const int mod=1e9+7;
int x,y;
int main()
{
// freopen("test.in","r",stdin);
// freopen("output.in", "w", stdout);
cin>>x>>y;
if(x==y) cout<<x<<'\n';
else cout<<3-x-y<<'\n';
return 0;
}
G - Roping the Field

 Give the coordinates of multiple points , Is the coordinates of each fence , There are also the center coordinates and radii of several strange circles , Connect the fence with ropes , But the rope can't go through the strange circle , And the ropes shall not intersect , Ask how many can be connected .
Give the coordinates of multiple points , Is the coordinates of each fence , There are also the center coordinates and radii of several strange circles , Connect the fence with ropes , But the rope can't go through the strange circle , And the ropes shall not intersect , Ask how many can be connected .
Ideas : It seems that the problem is a geometric problem . First consider how not to connect the rope on the strange circle . That is, the shortest distance from the center of the strange circle to each rope should be greater than the radius , That is the distance from the preprocessing point to the line segment , One of the previous questions involves . The rest is about how you can connect up to , namely DP problem , Then consider the interval DP. Section DP The part is not difficult to write , But it is mainly the pretreatment part that needs to be considered , The last is to meet the requirements of not crossing .
AC Code :
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <stack>
#include <vector>
#include <map>
#include <queue>
#include <cstring>
#include <cmath>
#include <set>
#include <iterator>
using namespace std;
typedef long long ll;
#define ios ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define INF 0x3f3f3f3f
#define ept 1e-6
// Determine whether it is necessary to open ll!!!
// Determine whether initialization is required !!!
const int mod=1e9+7;
const int N=200;
double R;
int n,m;
int f[N][N];
bool vis[N][N];
struct node
{
double x,y;
} a[N],b[N];
double len(node a,node b)
{
return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
double distance(node u,node v,node w)
{
double cc=0;
double a,b,c;
a=len(u,v);
b=len(v,w);
c=len(u,w);
if(c<=ept||b<=ept)
{
cc=0;
return cc;
}
if(a<=ept)
{
cc=b;
return cc;
}
if(c*c>=a*a+b*b)
{
cc=b;
return cc;
}
if(b*b>=a*a+c*c)
{
cc=c;
return cc;
}
double p=(a+b+c)/2;
double s=sqrt(p*(p-a)*(p-b)*(p-c));
cc=2*s/a;
return cc;
}
bool judge(node a,node b,node c)
{
double dd=distance(a,b,c);
if(dd>R) return 0;
return 1;
}
bool check(node u,node v)
{
for(int i=1;i<=m;i++)
{
if(judge(u,v,b[i]))
return 0;
}
return 1;
}
int main()
{
// freopen("test.in","r",stdin);
// freopen("output.in", "w", stdout);
cin>>n>>m>>R;
for(int i=1;i<=n;i++)
cin>>a[i].x>>a[i].y;
for(int i=1;i<=m;i++)
cin>>b[i].x>>b[i].y;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
if(i==j) continue;
vis[i][j]=check(a[i],a[j]);// Preprocessing two-dimensional matrix , That is, there are several lines that can be connected according to the strange circle
}
}
for(int l=3;l<=n;l++)// The minimum interval length is 3
{
for(int i=1;i<=n-l+1;i++)
{
for(int j=i;j<=i+l-1;j++)//j Is the interval breakpoint
{
f[i][i+l-1]=max(f[i][i+l-1],f[i][j]+f[j][i+l-1]);
}
if(vis[i][i+l-1]&&(i!=1||i+l-1!=n))
f[i][i+l-1]++;// Update the value of each interval
}
}
cout<<f[1][n]<<'\n';
return 0;
}
H - Cooking

There are several dishes that take different times to complete , Now there are two ovens , Ask how long it will take at least .
Ideas :01 knapsack problem , The upper limit of the backpack is the sum of all dishes divided by two .
AC Code :
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define ios ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define INF 0x3f3f3f3f
// Determine whether it is necessary to open ll!!!
// Determine whether initialization is required !!!
const int mod=1e9+7;
const int N=105;
int n;
int t[N],ans;
int f[1000005];
int main()
{
// freopen("test.in","r",stdin);
// freopen("output.in", "w", stdout);
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>t[i];
ans+=t[i];
}
for(int i=1;i<=n;i++)
{
for(int j=ans/2;j>=t[i];j--)
{
if(j>=t[i])
f[j]=max(f[j],f[j-t[i]]+t[i]);
}
}
cout<<ans-f[ans/2]<<'\n';
return 0;
}
os: The one that impressed me deeply in the winter vacation question ,,,
J - Rush Hour 2


Given four numbers , from A To B, Time used is C, because traffic jam, One more time is  ,t It's time to leave , ask 1~N The shortest possible time .
,t It's time to leave , ask 1~N The shortest possible time .
Ideas : It can be seen that it is the shortest circuit problem , But time needs attention , Because we have given the time-dependent equation , So choose the shortest time to walk . We can use the mean inequality a+b>=2*sqrt(a*b), Come to the conclusion t=sqrt(D)-1 It takes the shortest time to start , So when the arrival time is less than this , You can wait until that time ; If the arrival time is greater than this point , Go directly because the data range is large , Use chained forward star storage map .
AC Code :
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define ios ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define INF 0x3f3f3f3f3f3f3f3f
// Determine whether it is necessary to open ll!!!
// Determine whether initialization is required !!!
const int mod=1e9+7;
const ll N=1e5+5;
ll n,m,a,b,c2,d2;
ll to[N<<1],c[N<<1],d[N<<1],nex[N<<1],head[N],vis[N<<1];
ll dis[N<<1],cnt;
void add_edge(ll a,ll b,ll c1,ll d1)
{
to[++cnt]=b;
c[cnt]=c1;
d[cnt]=d1;
nex[cnt]=head[a];
head[a]=cnt;
}
void Dijkstra(){
fill(dis,dis+(N<<1),INF);
dis[1]=0;
priority_queue<pair<ll,ll>,vector<pair<ll,ll>>,greater<pair<ll,ll>>>q;
q.push({0,1});
while(q.size())
{
pair<ll,ll>p=q.top();
q.pop();
if(vis[p.second]) continue;
vis[p.second]=1;
for(ll i=head[p.second];i;i=nex[i])
{
ll best=INF;
ll j=to[i];
ll x=(ll)sqrt(1.0*d[i]);
ll L=max(dis[p.second],x),R=x;
R=max(R,L);
for(ll t=L;t<=R;t++){
ll s=t+c[i]+d[i]/(t+1);
best=min(best,s);
}
if(dis[j]>best){
dis[j]=best;
q.push({best,j});
}
}
}
}
int main()
{
// freopen("test.in","r",stdin);
// freopen("output.in", "w", stdout);
//ios;
cin>>n>>m;
for(ll i=0;i<m;i++)
{
cin>>a>>b>>c2>>d2;
add_edge(a,b,c2,d2);
add_edge(b,a,c2,d2);
}
Dijkstra();
if(dis[n]==INF) cout<<-1<<'\n';
else cout<<dis[n]<<'\n';
return 0;
}边栏推荐
- Basic operation of graph (C language)
- 完好性简要介绍
- Gcache of goframe memory cache
- 移动端——swipe特效之图片时间轴
- Three years of college should be like this
- swiper——单页面多轮播插件冲突解决方案
- Analysis of the implementation principle of an open source markdown to rich text editor
- 分类统计字符个数 (15 分)
- Is it safe for qiniu business school to send Huatai account? Really?
- IEEE floating point mantissa even round - round to double
猜你喜欢

2022 online summit of emerging market brands going to sea will be held soon advance AI CEO Shou Dong will be invited to attend

Php+mysql library management system (course design)
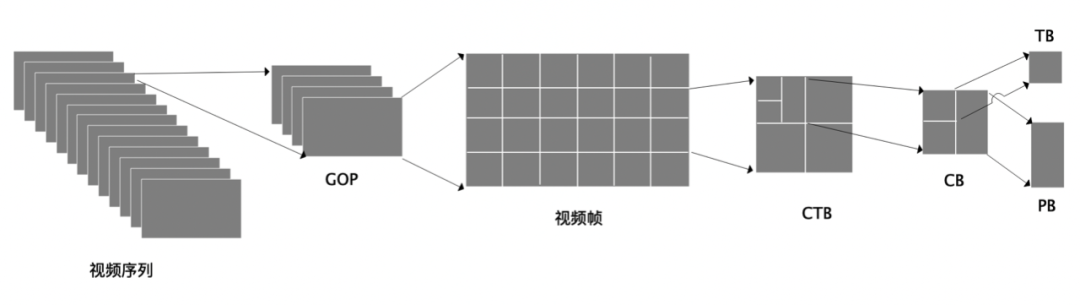
H.265编码原理入门

Svn deploys servers and cleints locally and uses alicloud disks for automatic backup

Games-101 闫令琪 5-6讲 光栅化处理 (笔记整理)
Gcache of goframe memory cache

Super Codex from the open source world, the authoritative release of China's open source Codex list!

The key to the safe was inserted into the door, and the college students stole the mobile phone numbers of 1.1 billion users of Taobao alone

Learn to crawl for a month and earn 6000 a month? Don't be fooled. The teacher told you the truth about the reptile

Cloudcompare source code analysis: read ply file
随机推荐
What is deadlock? (explain the deadlock to everyone and know what it is, why it is used and how to use it)
【NodeJs】Electron安装
Exercise 8-5 using functions to realize partial copying of strings (20 points)
向线程池提交任务
Learn to crawl for a month and earn 6000 a month? Don't be fooled. The teacher told you the truth about the reptile
Exercise 11-3 calculate the longest string length (15 points)
Php+mysql library management system (course design)
[bitbear story collection] February MVP hero story open source with love
Tkinter study notes (IV)
习题6-2 使用函数求特殊a串数列和 (20 分)
华为云、OBS、
Huawei equipment configuration hovpn
Exercise 9-5 address book sorting (20 points)
R7-1 列表或元组的数字元素求和
360 online enterprise security cloud is open to small, medium and micro enterprises for free
Daily question -1317 Converts an integer to the sum of two zero free integers
MATLAB点云处理(二十五):点云生成 DEM(pc2dem)
leetcode 257. Binary Tree Paths 二叉树的所有路径(简单)
批改网高分短语&句型
Inventory | more than 20 typical security incidents occurred in February, with a loss of nearly $400million
