当前位置:网站首页>22/8/4 记忆化搜索+博弈论
22/8/4 记忆化搜索+博弈论
2022-08-04 17:48:00 【咸蛋_dd】
目录
1.记忆化搜索——滑雪
给定一个 RR 行 CC 列的矩阵,表示一个矩形网格滑雪场。
矩阵中第 ii 行第 jj 列的点表示滑雪场的第 ii 行第 jj 列区域的高度。
一个人从滑雪场中的某个区域内出发,每次可以向上下左右任意一个方向滑动一个单位距离。
当然,一个人能够滑动到某相邻区域的前提是该区域的高度低于自己目前所在区域的高度。
下面给出一个矩阵作为例子:
1 2 3 4 5 16 17 18 19 6 15 24 25 20 7 14 23 22 21 8 13 12 11 10 9在给定矩阵中,一条可行的滑行轨迹为 24−17−2−124−17−2−1。
在给定矩阵中,最长的滑行轨迹为 25−24−23−…−3−2−125−24−23−…−3−2−1,沿途共经过 2525 个区域。
现在给定你一个二维矩阵表示滑雪场各区域的高度,请你找出在该滑雪场中能够完成的最长滑雪轨迹,并输出其长度(可经过最大区域数)。
输入格式
第一行包含两个整数 RR 和 CC。
接下来 RR 行,每行包含 CC 个整数,表示完整的二维矩阵。
输出格式
输出一个整数,表示可完成的最长滑雪长度。
数据范围
1≤R,C≤3001≤R,C≤300,
0≤矩阵中整数≤10000
#include <bits/stdc++.h>
using namespace std;
const int N=310;
int n,m;
int g[N][N];
int f[N][N];
int dx[4]={-1,0,1,0};
int dy[4]={0,1,0,-1};
int dp(int x,int y)
{
int &v=f[x][y];
if(f[x][y]!=-1) return f[x][y];
v=1;
for(int i=0;i<4;i++)
{
int a=x+dx[i];
int b=y+dy[i];
if(a>=1&&a<=n&&b>=1&&b<=m&&g[a][b]<g[x][y])
v=max(v,dp(a,b)+1);
}
return v;
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
scanf("%d",&g[i][j]);
memset(f,-1,sizeof(f));
int res=0;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
res=max(res,dp(i,j));
printf("%d\n",res);
return 0;
}2.博弈论-- Nim游戏
给定 nn 堆石子,两位玩家轮流操作,每次操作可以从任意一堆石子中拿走任意数量的石子(可以拿完,但不能不拿),最后无法进行操作的人视为失败。
问如果两人都采用最优策略,先手是否必胜。
输入格式
第一行包含整数 nn。
第二行包含 nn 个数字,其中第 ii 个数字表示第 ii 堆石子的数量。
输出格式
如果先手方必胜,则输出
Yes。否则,输出
No。数据范围
1≤n≤1051≤n≤105,
1≤每堆石子数≤1091≤每堆石子数≤109输入样例:
2 2 3输出样例:
Yes
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
int main()
{
int n;
scanf("%d", &n);
int res = 0;
while (n -- )
{
int x;
scanf("%d", &x);
res ^= x;
}
if (res) puts("Yes");
else puts("No");
return 0;
}
3.博弈论-- 台阶-Nim游戏
现在,有一个 nn 级台阶的楼梯,每级台阶上都有若干个石子,其中第 ii 级台阶上有 aiai 个石子(i≥1i≥1)。
两位玩家轮流操作,每次操作可以从任意一级台阶上拿若干个石子放到下一级台阶中(不能不拿)。
已经拿到地面上的石子不能再拿,最后无法进行操作的人视为失败。
问如果两人都采用最优策略,先手是否必胜。
输入格式
第一行包含整数 nn。
第二行包含 nn 个整数,其中第 ii 个整数表示第 ii 级台阶上的石子数 aiai。
输出格式
如果先手方必胜,则输出
Yes。否则,输出
No。数据范围
1≤n≤1051≤n≤105,
1≤ai≤1091≤ai≤109输入样例:
3 2 1 3输出样例:
Yes#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
int main()
{
int n;
scanf("%d", &n);
int res = 0;
for (int i = 1; i <= n; i ++ )
{
int x;
scanf("%d", &x);
if (i & 1) res ^= x;
}
if (res) puts("Yes");
else puts("No");
return 0;
}
4.博弈论--AcWing 893. 集合-Nim游戏
给定 nn 堆石子以及一个由 kk 个不同正整数构成的数字集合 SS。
现在有两位玩家轮流操作,每次操作可以从任意一堆石子中拿取石子,每次拿取的石子数量必须包含于集合 SS,最后无法进行操作的人视为失败。
问如果两人都采用最优策略,先手是否必胜。
输入格式
第一行包含整数 kk,表示数字集合 SS 中数字的个数。
第二行包含 kk 个整数,其中第 ii 个整数表示数字集合 SS 中的第 ii 个数 sisi。
第三行包含整数 nn。
第四行包含 nn 个整数,其中第 ii 个整数表示第 ii 堆石子的数量 hihi。
输出格式
如果先手方必胜,则输出
Yes。否则,输出
No。数据范围
1≤n,k≤1001≤n,k≤100,
1≤si,hi≤100001≤si,hi≤10000输入样例:
2 2 5 3 2 4 7输出样例:
Yes#include <bits/stdc++.h>
#include <unordered_set>
using namespace std;
int n,m;
const int N=100010;
int f[N],s[N];
int sg(int x)//SG函数的应用
{
if(f[x]!=-1) return f[x];
unordered_set<int> S;//必须定义再递归里面,每次都是一个新的set
for(int i=0;i<m;i++)
{
int sum=s[i];
if(x>=sum) S.insert(sg(x-sum));
}
for(int i=0; ;i++)//遍历找出在集合之外的最小数
{
if(!S.count(i))
return f[x]=i;
}
}
int main()
{
cin>>m;
for(int i=0;i<m;i++) cin>>s[i];
cin>>n;
memset(f,-1,sizeof(f));
int res=0;
for(int i=0;i<n;i++)
{
int x;
cin>>x;
res^=sg(x);//将每个图分别求SG函数,然后异或,如果是0就是必败态,反之就是必胜态
}
if(res) puts("Yes");
else puts("No");
return 0;
}5.博弈论--拆分-Nim游戏
给定 nn 堆石子,两位玩家轮流操作,每次操作可以取走其中的一堆石子,然后放入两堆规模更小的石子(新堆规模可以为 00,且两个新堆的石子总数可以大于取走的那堆石子数),最后无法进行操作的人视为失败。
问如果两人都采用最优策略,先手是否必胜。
输入格式
第一行包含整数 nn。
第二行包含 nn 个整数,其中第 ii 个整数表示第 ii 堆石子的数量 aiai。
输出格式
如果先手方必胜,则输出
Yes。否则,输出
No。数据范围
1≤n,ai≤1001≤n,ai≤100
输入样例:
2 2 3输出样例:
Yes
#include <bits/stdc++.h>
#include <unordered_set>
using namespace std;
const int N=110;
int f[N];
int n;
int sg(int x)
{
if(f[x]!=-1) return f[x];
unordered_set<int> S;
for(int i=0;i<x;i++)
{
for(int j=0;j<=i;j++)
S.insert(sg(i)^sg(j));
}
for(int i=0;;i++)
{
if(!S.count(i))
return f[x]=i;
}
}
int main()
{
cin>>n;
memset(f,-1,sizeof(f));
int res=0;
while(n--)
{
int x;
cin>>x;
res^=sg(x);
}
if(res) puts("Yes");
else puts("No");
return 0;
}
边栏推荐
- CAS:385437-57-0,DSPE-PEG-Biotin,生物活性分子磷脂-聚乙二醇-生物素
- Cholesterol-PEG-DBCO,CLS-PEG-DBCO,胆固醇-聚乙二醇-二苯基环辛炔科研试剂
- clickhouse 上下线表
- 信息系统项目管理师必背核心考点(六十)项目集管理
- IDEA以多端口启动同一个服务项目
- Boosting之GBDT原理
- 【日记】mysql数据库连接池
- 要有遥不可及的梦想,也要有脚踏实地的本事
- R语言缺失时间序列的填充及合并:补齐时间序列数据中所有缺失的时间索引、使用merge函数合并日期补齐之后的时间序列数据和另外一个时间序列数据(补齐左侧数据)
- Flutter实战-请求封装(四)之gzip报文压缩
猜你喜欢
LVS+Keepalived群集
Thrift IDL示例文件

.NET云原生应用发展论坛--8月7日邀你一起云上探索

《机器学习的随机矩阵方法》
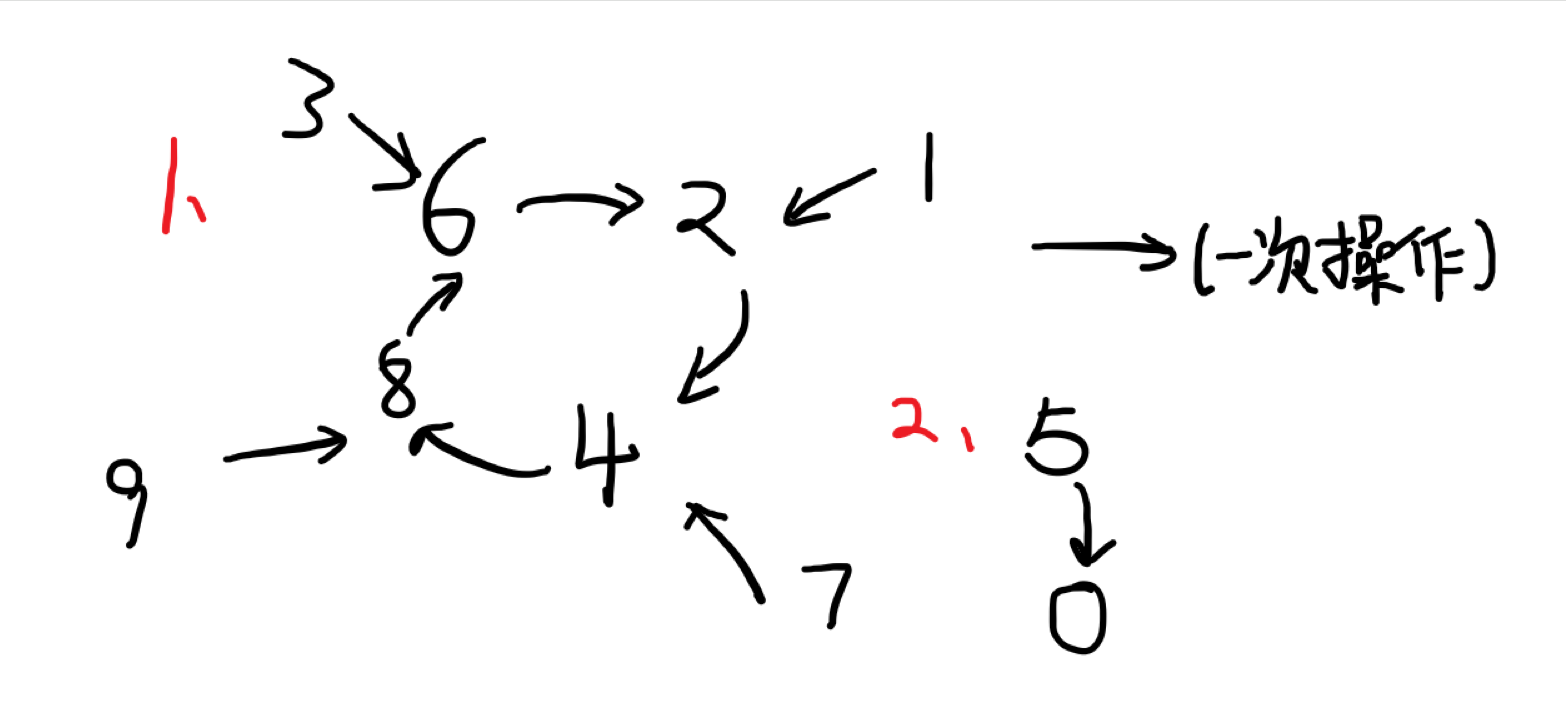
Codeforces Round #811 (Div. 3)
如何让 JS 代码不可断点
Digital-intelligent supply chain management system for chemical manufacturing industry: build a smart supply system and empower enterprises to improve production efficiency

How to make JS code unbreakable

谷歌开源芯片 180 纳米制造工艺

OpenInfra Days China 2022 | SelectDB to share with you the Apache Doris in Internet advertising business practices
随机推荐
The prefix and discretization
R语言ggpubr包的ggtexttable函数可视化表格数据(直接绘制表格图或者在图像中添加表格数据)、使用ggarrange函数将表格数据和可视化图像组合起来(表格数据在可视化图像下方)
Thrift IDL示例文件
网络靶场监控系统的安全加固纪实(1)—SSL/TLS对日志数据加密传输
arm交叉编译
区间贪心(区间合并)
Cron表达式
面试官:可以谈谈乐观锁和悲观锁吗
leetcode 13. 罗马数字转整数
树莓派通过API向企业微信推送图文
JS兼容问题总结
localstorage本地存储的方法
悦刻难回巅峰
C# Sqlite database construction and use skills
动态数组底层是如何实现的
要有遥不可及的梦想,也要有脚踏实地的本事
LeetCode 899. 有序队列
太一集团全资收购火币旗下社交产品火信
R语言使用ggpubr包的ggsummarystats函数可视化柱状图(通过ggfunc参数设置)、在可视化图像的下方添加描述性统计结果表格、palette参数配置柱状图及统计数据的颜色
leetcode 14. 最长公共前缀