当前位置:网站首页>[combinatorics] generating function (generating function application scenario | using generating function to solve recursive equation)
[combinatorics] generating function (generating function application scenario | using generating function to solve recursive equation)
2022-07-03 17:57:00 【Programmer community】
List of articles
- One 、 Generate function application scenarios
- Two 、 Solving recursive equations using generating functions
Reference blog :
- 【 Combinatorial mathematics 】 Generating function Brief introduction ( Generating function definition | Newton's binomial coefficient | Common generating functions | Related to constants | Related to binomial coefficient | Related to polynomial coefficients )
- 【 Combinatorial mathematics 】 Generating function ( Linear properties | Product properties )
- 【 Combinatorial mathematics 】 Generating function ( Shift property )
- 【 Combinatorial mathematics 】 Generating function ( The nature of summation )
- 【 Combinatorial mathematics 】 Generating function ( Commutative properties | Derivative property | Integral properties )
- 【 Combinatorial mathematics 】 Generating function ( Summary of nature | Important generating functions ) *
- 【 Combinatorial mathematics 】 Generating function ( Generate function examples | Given the general term formula, find the generating function | Given the generating function, find the general term formula )
One 、 Generate function application scenarios
Generate function application scenarios :
- Solve the recursive equation
- Multiple sets
r
r
r Combination count
- The number of solutions of the indefinite equation
- integer partition
Multiple sets
r
r
r Combination count , Before Only the number of combinations in special cases can be counted , That is, the selected number
r
r
r Less than the repetition of each term of the multiple set , Only then Combinatorial number
N
=
C
(
k
+
r
−
1
,
r
)
N= C(k + r - 1, r)
N=C(k+r−1,r), If
r
r
r Greater than repeatability , You need to use the generating function to solve ;
The number of solutions of the indefinite equation , Before, we can only solve Without constraints , If there are constraints on variables , Such as
x
1
x_1
x1 Values can only be taken in a certain interval , In this case , You must use the generating function to solve ;
integer partition , Split a positive number into the sum of several integers , Number of splitting schemes , It can also be calculated by generating functions ;
Review multiple set permutations :
- Repeatable elements , Orderly selection , Corresponding Arrangement of multiple sets ;
whole
row
Column
=
n
!
n
1
!
n
2
!
⋯
n
k
!
Full Permutation = \cfrac{n!}{n_1! n_2! \cdots n_k!}
whole row Column =n1!n2!⋯nk!n! , Incomplete permutation
k
r
,
r
≤
n
i
k^r , \ \ r\leq n_i
kr, r≤ni
- Repeatable elements , Unordered selection , Corresponding Combination of multiple sets ;
N
=
C
(
k
+
r
−
1
,
r
)
N= C(k + r - 1, r)
N=C(k+r−1,r)
Two 、 Solving recursive equations using generating functions
Recurrence equation :
a
n
−
5
a
n
−
1
+
6
a
n
−
2
=
0
a_n - 5a_{n-1} + 6a_{n-2} = 0
an−5an−1+6an−2=0
initial value :
a
0
=
1
,
a
1
=
2
a_0 = 1, a_1 = 2
a0=1,a1=2
{
a
n
}
\{a_n\}
{ an} Number sequence is
{
a
0
,
a
1
,
a
2
,
a
3
,
⋯
,
a
n
,
⋯
}
\{ a_0 , a_1, a_2, a_3 , \cdots , a_n , \cdots\}
{ a0,a1,a2,a3,⋯,an,⋯}
a
n
a_n
an The corresponding generating function is
G
(
x
)
=
a
0
+
a
1
x
+
a
2
x
2
+
a
3
x
3
+
⋯
G(x) = a_0 + a_1 x + a_2 x^2 + a_3x^3 + \cdots
G(x)=a0+a1x+a2x2+a3x3+⋯
According to the recursive equation , At the same time, in order to make the following items can be about , Use
−
5
x
-5x
−5x multiply
G
(
x
)
G(x)
G(x) Generating function , Use
+
6
x
2
+6x^2
+6x2 multiply
G
(
x
)
G(x)
G(x) , Get the following three formulas ,
−
5
x
-5x
−5x multiply
G
(
x
)
G(x)
G(x) The first thing you get is
x
x
x The first power term of , Map this item to
G
(
x
)
G(x)
G(x) Medium
x
x
x Under the power term ,
+
6
x
2
+6x^2
+6x2 multiply
G
(
x
)
G(x)
G(x) The first thing you get is
x
x
x The quadratic term of , Map this item to
G
(
x
)
G(x)
G(x) Medium
x
x
x Under the quadratic term ;
G
(
x
)
=
a
0
+
a
1
x
+
a
2
x
2
+
a
3
x
3
+
⋯
\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ G(x) = a_0 + a_1 x + a_2 x^2 + a_3x^3 + \cdots
G(x)=a0+a1x+a2x2+a3x3+⋯
−
5
x
G
(
x
)
=
−
5
a
0
x
−
5
a
1
x
2
−
5
a
2
x
3
−
⋯
\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -5x \ G(x) = \ \ \ \ -5a_0x - 5a_1x^2 - 5a_2x^3 - \cdots
−5x G(x)= −5a0x−5a1x2−5a2x3−⋯
6
x
2
G
(
x
)
=
+
6
a
0
x
2
+
6
a
x
3
+
⋯
\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 6x^2 \,G(x) = \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ + \,6a_0x^2 + 6a_x^3 + \cdots
6x2G(x)= +6a0x2+6ax3+⋯
(
1
−
5
x
+
6
x
2
)
G
(
x
)
=
a
0
+
(
a
1
−
5
a
0
)
x
(1-5x+6x^2)G(x) =a_0 + (a_1 - 5a_0)x
(1−5x+6x2)G(x)=a0+(a1−5a0)x
The formula below the above horizontal line is Above the horizontal line The result of adding the three formulas ;
Observe the above right The third column , The red box in the picture ;
After the above power alignment , The third column to the right of the appearing equal sign
+
a
2
x
2
−
5
a
1
x
2
+
6
a
0
x
2
+ a_2 x^2 -5a_1x^2 + \,6a_0x^2
+a2x2−5a1x2+6a0x2 , Will the
x
2
x^2
x2 Extract to get
(
a
2
−
5
a
1
+
6
a
0
)
x
2
(a_2 - 5a_1 + 6a_0)x^2
(a2−5a1+6a0)x2 , It just corresponds to the recursive equation
a
n
−
5
a
n
−
1
+
6
a
n
−
2
=
0
a_n - 5a_{n-1} + 6a_{n-2} = 0
an−5an−1+6an−2=0 ,
So there is
a
2
−
5
a
1
+
6
a
0
=
0
a_2 - 5a_1 + 6a_0 = 0
a2−5a1+6a0=0 , Then you can get
(
a
2
−
5
a
1
+
6
a
0
)
x
2
=
0
(a_2 - 5a_1 + 6a_0)x^2 = 0
(a2−5a1+6a0)x2=0
From this we can see that , If all three formulas are added , The figure below Inside the blue rectangle on the right , All of them are
0
0
0 ;

At present, only
a
0
+
a
1
x
−
5
a
0
x
a_0 + a_1x -5a_0x
a0+a1x−5a0x Three items ; Among them
a
0
=
1
,
a
1
=
−
2
a_0 = 1 , a_1 = -2
a0=1,a1=−2 Is the initial value ;
On the right side of the final equation is :
1
−
2
x
−
5
x
=
1
−
7
x
1 - 2x - 5x = 1-7x
1−2x−5x=1−7x
Substitute the above formula into
(
1
−
5
x
+
6
x
2
)
G
(
x
)
=
a
0
+
(
a
1
−
5
a
0
)
x
(1-5x+6x^2)G(x) =a_0 + (a_1 - 5a_0)x
(1−5x+6x2)G(x)=a0+(a1−5a0)x in , Use
1
−
2
x
−
5
x
=
1
−
7
x
1 - 2x - 5x = 1-7x
1−2x−5x=1−7x Replace the formula on the right side of the equation , obtain :
(
1
−
5
x
+
6
x
2
)
G
(
x
)
=
1
−
7
x
(1-5x+6x^2)G(x) =1-7x
(1−5x+6x2)G(x)=1−7x
G
(
x
)
=
1
−
7
x
1
−
5
x
+
6
x
2
G(x) = \cfrac{1-7x}{1-5x+6x^2}
G(x)=1−5x+6x21−7x
Use Given Generating function , Find the corresponding series Of Method , Expand the above formula , Reference resources 【 Combinatorial mathematics 】 Generating function ( Generate function examples | Given the general term formula, find the generating function | Given the generating function, find the general term formula ) Two 、 Calculate the series given the generating function Method ,
First factorize the denominator , Then set two undetermined coefficients , After passing points , according to
x
x
x Write the equations with the term coefficients , Finally solve the equations , In the end, you can get :
G
(
x
)
=
1
−
7
x
1
−
5
x
+
6
x
2
=
5
1
−
2
x
−
4
1
−
3
x
G(x) = \cfrac{1-7x}{1-5x+6x^2} = \cfrac{5}{1-2x} - \cfrac{4}{1-3x}
G(x)=1−5x+6x21−7x=1−2x5−1−3x4
5
1
−
2
x
\cfrac{5}{1-2x}
1−2x5 The corresponding series is :
∑
n
=
0
∞
5
(
2
x
)
n
=
5
∑
n
=
0
∞
2
n
x
n
\sum\limits_{n=0}^\infty 5 (2x)^n = 5\sum\limits_{n=0}^\infty 2^n x^n
n=0∑∞5(2x)n=5n=0∑∞2nxn
4
1
−
3
x
\cfrac{4}{1-3x}
1−3x4 The corresponding series is :
∑
n
=
0
∞
(
−
4
)
(
3
x
)
n
=
−
4
∑
n
=
0
∞
3
n
x
n
\sum\limits_{n=0}^\infty (-4) (3x)^n = -4\sum\limits_{n=0}^\infty 3^n x^n
n=0∑∞(−4)(3x)n=−4n=0∑∞3nxn
The series form of the final generated function is :
G
(
x
)
=
5
∑
n
=
0
∞
2
n
x
n
−
4
∑
n
=
0
∞
3
n
x
n
G(x) = 5\sum\limits_{n=0}^\infty 2^n x^n - 4\sum\limits_{n=0}^\infty 3^n x^n
G(x)=5n=0∑∞2nxn−4n=0∑∞3nxn
General solution of recurrence equation :
a
n
=
5
⋅
2
n
−
4
⋅
3
n
a_n = 5 \cdot 2^n - 4 \cdot 3^n
an=5⋅2n−4⋅3n
The basic idea : There is the original recursive equation , Derive the recurrence equation about the generating function ;
边栏推荐
- [LINUX]CentOS 7 安装MYSQL时报错“No package mysql-server available“No package zabbix-server-mysql availabl
- Analyse ArrayList 3: suppression d'éléments
- win32:堆破坏的dump文件分析
- Five problems of database operation in commodity supermarket system
- 小程序 多tab 多swiper + 每个tab分页
- [tutorial] build your first application on coreos
- Classroom attendance system based on face recognition tkinter+openpyxl+face_ recognition
- Vs2013 has blocked the installer, and ie10 needs to be installed
- Win32: dump file analysis of heap corruption
- Discussion sur la logique de conception et de mise en oeuvre du processus de paiement
猜你喜欢

Win32: dump file analysis of heap corruption
![[combinatorics] generating function (summation property)](/img/74/e6ef8ee69ed07d62df9f213c015f2c.jpg)
[combinatorics] generating function (summation property)

Deops入门
互联网医院HIS管理平台源码,在线问诊,预约挂号 智慧医院小程序源码

Global and Chinese health care OEM and ODM market status survey and investment planning recommendations report 2022-2028

TCP拥塞控制详解 | 3. 设计空间

PHP MySQL create database

IntelliJ 2021.3 short command line when running applications

Win32: analyse du fichier dump pour la défaillance du tas
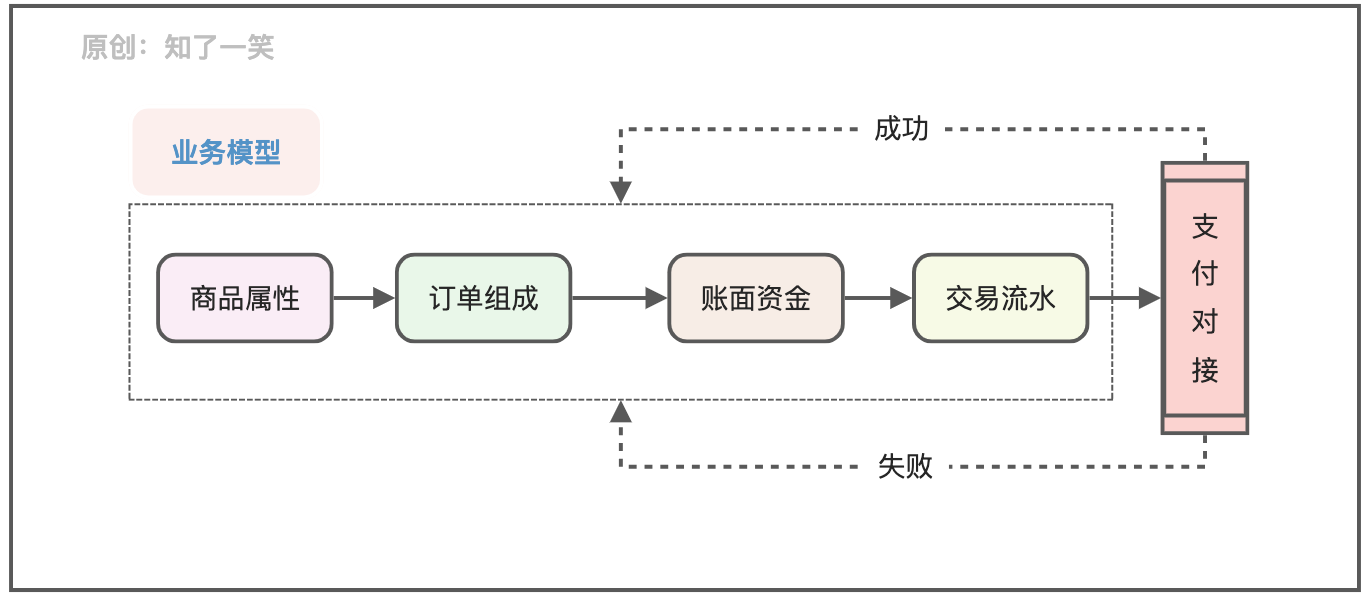
聊聊支付流程的设计与实现逻辑
随机推荐
自动渗透测试工具核心功能简述
Leetcode 538 converts binary search tree into cumulative tree -- recursive method and iterative method
PHP processing - watermark images (text, etc.)
win32:堆破壞的dump文件分析
远程办公工具分享|社区征文
AcWing 271. 杨老师的照相排列【多维DP】
Fedora 21 installs lamp host server
Analysis report on production and marketing demand and investment forecast of China's PVC industry from 2021 to 2026
PHP MySQL preprocessing statement
Ml (machine learning) softmax function to realize the classification of simple movie categories
Interviewer: why is the value nil not equal to nil?
WEB-UI自动化测试-最全元素定位方法
[combinatorics] recursive equation (summary of the solution process of recursive equation | homogeneous | double root | non-homogeneous | characteristic root is 1 | exponential form | the bottom is th
PUT vs. POST for Uploading Files - RESTful API to be Built Using Zend Framework
PHP MySQL create database
模块九作业
网格图中递增路径的数目[dfs逆向路径+记忆dfs]
Investigation on the operation prospect of the global and Chinese Anti enkephalinase market and analysis report on the investment strategy of the 14th five year plan 2022-2028
[教程]在 CoreOS 上构建你的第一个应用
c# .net 工具生态