当前位置:网站首页>【CNN基础】转置卷积学习笔记
【CNN基础】转置卷积学习笔记
2022-08-04 07:37:00 【sin(豪)】
目录
1. 转置卷积的直观理解
1.1 卷积和转置卷积
卷积的直观理解:卷积用来抽取输入的特征,底层的卷积抽取的是纹理、颜色等底层特征,上层的卷积抽取的是语义特征。卷积的输出一般称为feature map,在pytorch中一般为四维的tensor:[B, C, H, W],其中,
| B | batch size,一个小批量中的图片个数 |
|---|---|
| C | 通道数,输入图片一般有R,G,B三个通道,一般情况下后续feature map的H和W减少, 通道数C增加,保证信息不损失 |
| H,W | feature map的高H和宽W |
卷积我们可以看作是将输入图片的H和W逐层减少,通道数C逐层增加的操作。
转置卷积的直观理解:转置卷积直观上是想将H和W较小的feature map还原到输入图像尺寸的过程。注意,只是将尺寸还原到和输入图像相同,具体的权重是不同的。这样做是因为在某些应用如语义分割中,最后要求的输出是一个和输入尺寸相同的feature map,而不是像图像分类要求的输出是一个一维的tensor。
简单来说:
1. 卷积是让feature map尺寸减小,通道数增加;而转置卷积是让feature map尺寸增大,通道数减小。
2.卷积做下采样,转置卷积做上采用。
3. 如果卷积操作使得输入feature map由(h, w)变为(h’, w’),则同样超参数下,转置卷积操作会使得feature map由(h’, w’)变为(h, w)。
2. 转置卷积的计算过程
我之前写了计算卷积操作输出Feature Map的size和计算机如何计算卷积操作。
下面介绍两种计算转置卷积输出结果的思路。
2.1 思路一:将转置卷积看成几个矩阵相加
假设转置卷积的步幅stride=1,填充padding=0。假设输入为X,卷积核为K,输出为Y,则: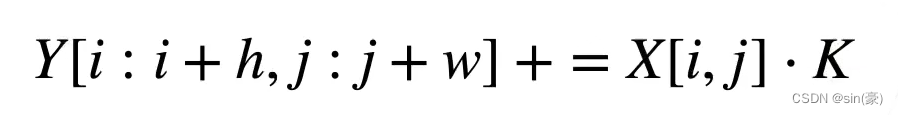
其中,h,w为卷积核的高和宽,下面的示意图比较容易看明白具体的含义: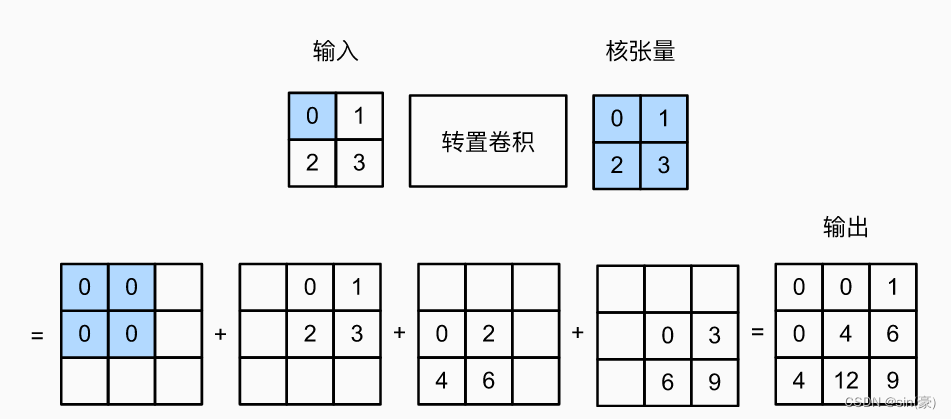
图片来源:【李沐】动手学深度学习
我们用pytorch简单实验下看看:
import torch
from torch import nn
X = torch.arange(4.).reshape(1, 1, 2, 2) # 从前到后分别代表:batch size, channel, h, w
K = torch.arange(4.).reshape(1, 1, 2, 2)
tconv = nn.ConvTranspose2d(1, 1, kernel_size=2, stride=1, padding=0, bias=False)
tconv.weight.data = K
print(f"X:\n{
X}\nK:\n{
tconv.weight.data}")
Y = tconv(X)
print(f"Y:\n{
Y.data}")
输出:
X:
tensor([[[[0., 1.],
[2., 3.]]]])
K:
tensor([[[[0., 1.],
[2., 3.]]]])
Y:
tensor([[[[ 0., 0., 1.],
[ 0., 4., 6.],
[ 4., 12., 9.]]]])
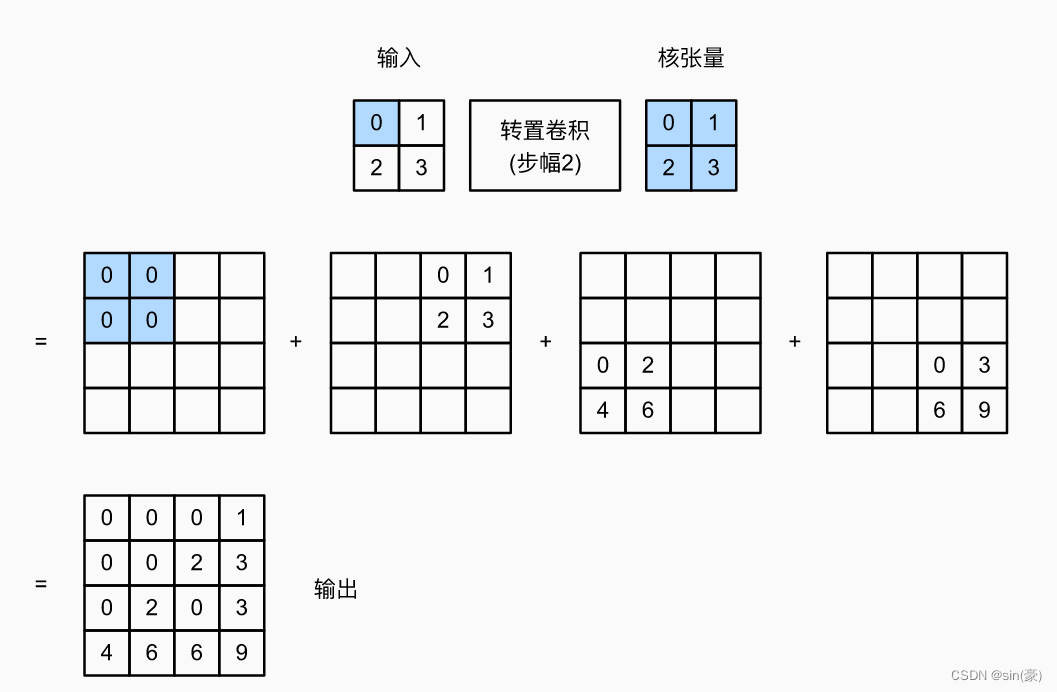
当stride=2, padding=0时,计算过程如下:
我们用pytorch简单实验下看看:
X = torch.arange(4.).reshape(1, 1, 2, 2) # 从前到后分别代表:batch size, channel, h, w
K = torch.arange(4.).reshape(1, 1, 2, 2)
tconv = nn.ConvTranspose2d(1, 1, kernel_size=2, stride=2, padding=0, bias=False)
tconv.weight.data = K
print(f"X:\n{
X}\nK:\n{
tconv.weight.data}")
Y = tconv(X)
print(f"Y:\n{
Y.data}")
输出:
X:
tensor([[[[0., 1.],
[2., 3.]]]])
K:
tensor([[[[0., 1.],
[2., 3.]]]])
Y:
tensor([[[[0., 0., 0., 1.],
[0., 0., 2., 3.],
[0., 2., 0., 3.],
[4., 6., 6., 9.]]]])
2.2 思路二:转置卷积是一种卷积
个人感觉这个计算思路更加通用一些,不需要像思路一一样涉及几个矩阵的相加,直接一开始就将转置卷积当作卷积来做。
p为填充padding,s为步幅stride,k为卷积核大小,则具体计算过程如下:

计算过程示意图为:
s = 1, p = 0, k = 2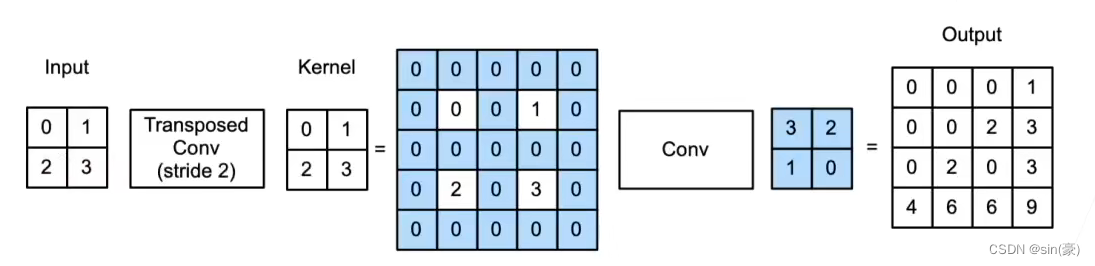
s = 1, p = 1, k = 3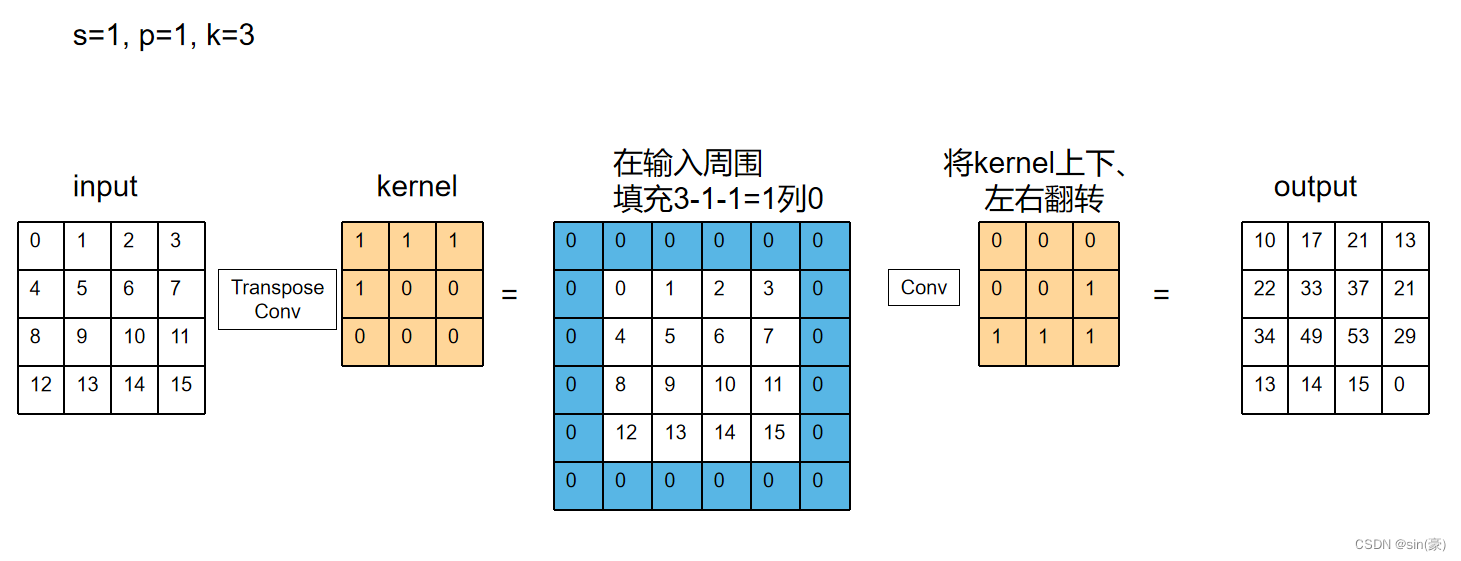
用Pytorch简单实验下:
X = torch.arange(16.).reshape(1, 1, 4, 4) # 从前到后分别代表:batch size, channel, h, w
K = torch.tensor([[1., 1., 1.], [1., 0., 0.], [0., 0., 0.]]).reshape(1, 1, 3, 3)
tconv = nn.ConvTranspose2d(1, 1, kernel_size=3, stride=1, padding=1, bias=False)
tconv.weight.data = K
print(f"X:\n{
X}\nK:\n{
tconv.weight.data}")
Y = tconv(X)
print(f"Y:\n{
Y.data}")
输出:
X:
tensor([[[[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.],
[12., 13., 14., 15.]]]])
K:
tensor([[[[1., 1., 1.],
[1., 0., 0.],
[0., 0., 0.]]]])
Y:
tensor([[[[10., 17., 21., 13.],
[22., 33., 37., 21.],
[34., 49., 53., 29.],
[13., 14., 15., 0.]]]])
3. 如何计算转置卷积输出feature map的size
我们规定:
| 符号 | 含义 |
|---|---|
| n | 输入feature map的高宽 |
| k | 转置卷积核的高宽 |
| p | 填充padding |
| s | 步幅stride |
则:转置卷积输出的feature map 的大小 n’ = sn + k - 2p - s
因此,如果想让高宽整数倍增加,则要求:k - 2p - s = 0,即k = 2p + s。
Pytorch做实验:
# n = 10, k = 64, s = 32, p = 16
X = torch.arange(100.).reshape(1, 1, 10, 10) # 从前到后分别代表:batch size, channel, h, w
tconv = nn.ConvTranspose2d(1, 1, kernel_size=64, stride=32, padding=16, bias=False)
Y = tconv(X)
Y.shape
输出:
torch.Size([1, 1, 320, 320])
可以看到输出size相较于输入扩大了32倍。(由10x10到320x320)
参考:
边栏推荐
猜你喜欢
随机推荐
金仓数据库KingbaseES客户端编程接口指南-JDBC(7. JDBC事务处理)
七牛云上传图片和本地上传
int *p = &a、p = &a、*p = a的正确理解
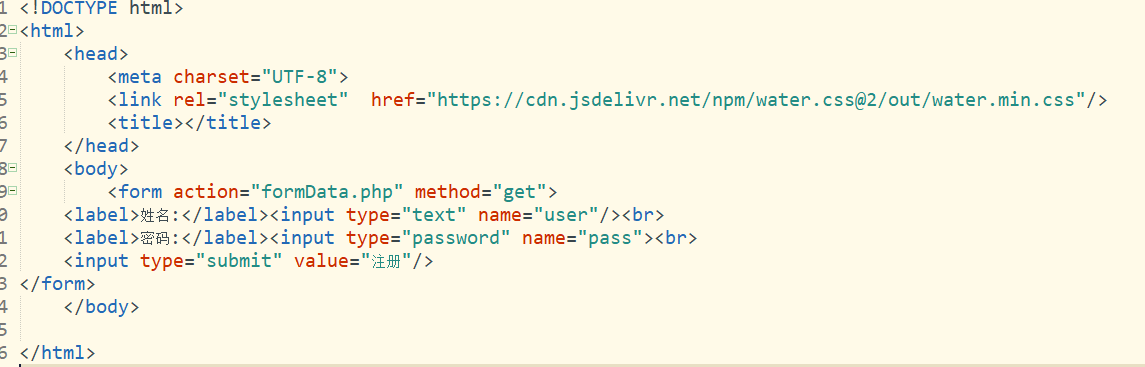
「PHP基础知识」转换数据类型
【JS 逆向百例】某网站加速乐 Cookie 混淆逆向详解
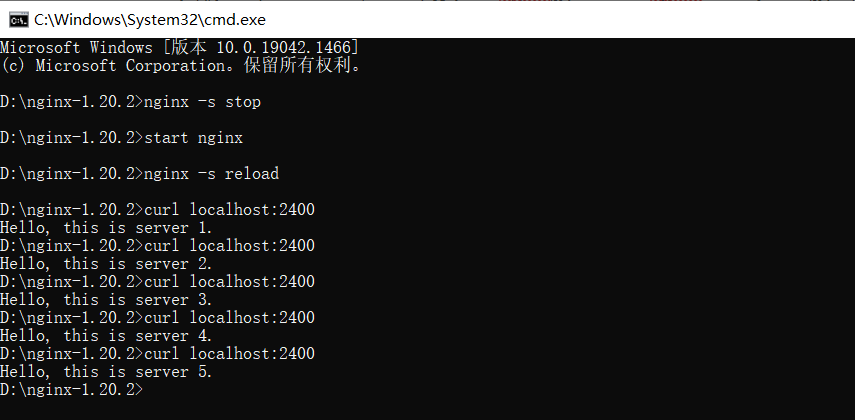
分布式计算实验1 负载均衡
unittest使用简述
C语言strchr()函数以及strstr()函数的实现
开发小技巧 navicate如何点击单元格显示全部的文本内容或通过图像查看内容
babylon 里面加gltf 模型
千古第一文人苏轼的众CP
app逆向1某联
The national vocational skills contest competition of network security emergency response
25.时间序列预测实战
两日总结五
【JS 逆向百例】某网站加速乐 Cookie 混淆逆向详解
Distributed Computing Experiment 1 Load Balancing
FCN - the originator of semantic segmentation (based on tf-Kersa reproduction code)
分布式计算实验2 线程池
The school to apply for link