当前位置:网站首页>8.电影评论分类:二分类问题
8.电影评论分类:二分类问题
2022-08-03 04:05:00 【好名字能更容易让朋友记住】
电影评论分类:二分类问题
加载IMDB数据集
IMDB数据集包含来自互联网电影数据库(IMDB)的50000条严重两极分化的评论。数据集分为用于训练的25000条评论与用于测试的25000条评论,训练集和测试集都包含50%的正面评论和50%的负面评论。
与MNIST数据集一样,IMDB数据集内置于Keras库。他已经经过预处理:评论(单词序列)已经被转换为整数序列,其中每个整数代表字典中的某个单词。
# 加载IMDB数据集
from keras.datasets import imdb
(train_data, train_labels), (test_data, test_labels) = imdb.load_data(num_words=10000)
# num_words=10000 的意思仅保留前10000个最常出现的单词。
train_data 和 test_data 这两个变量都是评论组成的列表,每条评论又是单词索引组成的列表(表示一系列单词)。
train_labels 和 test_labels 都是 0 和 1 组成的列表,其中 0 代表负面(negative),1 代表正面(positive)。
>>> train_data[0]
[1, 14, 22, 16, ... 178, 32]
>>> train_labels[0]
1
使用以下方法可以将评论解码为英语
word_index = imdb.get_word_index()
# 键值颠倒,将整数索引映射为单词
reverse_word_index = dict([(value, key) for (key, value) in word_index.items()])
# 索引减去了3,因为 0 为 padding(填充)、1 为 start of sequence(序列开始)、2 为 unknown(未知词)。
decoded_review = ' '.join([reverse_word_index.get(i - 3, '?') for i in train_data[0]])
decoded_review
准备数据
因为 train_data 中的数据为一个整数列表,所以不能直接输入神经网络。所以需要将列表转换为张量。转换方法有以下两种:
- 填充列表,使其具有相同的长度,再将列表转换成形状为(samples,word_indics)的整数张量,然后网络第一层使用能处理这种整数张量的层(即Embedding)。
- 对列表进行 one-hot 编码,将其转换为 0 和 1 组成的向量。举个例子,序列 [3, 5] 将会被转换为 10000维向量,只有索引为3和5的元素是1,其余都是0.然后网络第一层可以用 Dense 层,它能够处理浮点数向量数据。
接下来使用第二种方法将数据向量化。
# 将整数序列编码为二进制矩阵
import numpy as np
def vectorize_sequences(sequences, dimension=10000):
# 创建一个形状为(len(sequences), dimension)的零矩阵。
results = np.zeros((len(sequences), dimension))
# enumerate()函数,将sequences组合成一个索引序列,同时列出i(索引),sequence,并将i于sequence一一对应
# sequence为序列 sequences 为序列列表
for i, sequence in enumerate(sequences):
# 将reesult[i]的指定索引设为1
results[i, sequence] = 1.
return results
# 将训练数据向量化
x_train = vectorize_sequences(train_data)
# 将测试数据向量化
x_test = vectorize_sequences(test_data)
构建网络
对于输入数据是向量,而标签是标量(1和0),对于这种问题,使用带有 relu 激活的全连接层(Dense)的简单堆叠,比如
Dense(16, activation='relu')
传入 Dense 层的参数(16)是该层的隐藏单元的个数。一个隐藏单元是该层表示空间的一个维度。每个带有 relu 激活的 Dense 层都实现了下列张量运算:
output = relu(dot(W, input) + b)
16个隐藏单元对应的权重矩阵 W 的形状为 (input_dimension, 16) ,与 W 做点积相当于将输入数据投影到16维表示空间中(然后再加上偏置向量 b 并应用 relu 运算)。可以将表示空间的维度直观地理解为**“网络学习内部表示时所拥有的自由度”**。隐藏单元越多(即更高维的表示空间,网络能够学到更加复杂的表示,但网络的计算代价也变得更大,而且可能会导致学到不好的模式(这种模式会提高训练数据上的性能,但不会提高测试数据上的性能)。
对于 Dense 层的堆叠,你需要确定以下两个关键架构:
- 网络有多少层
- 每层有多少个隐藏单元
本次实验选择以下架构:
- 两个中间层,每层都会有16个隐藏单元。
- 第三层输出一个标量,预测当前评论的感情。
中间层使用 relu 作为激活函数,最后一层使用 sigmoid 激活以输出一个0~1范围内的概率值(表示样本的目标值等于1的可能性,即评论为正面的可能性)。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-sjC2HLez-1658325105885)(C:\Users\33219\Downloads\三层网络 (1)].png)
上图显示了网络的结构,用Keras实现
# 模型定义
from keras import models
from keras import layers
model = models.Sequential()
model.add(layers.Dense(16, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(16, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))
什么是激活函数?为什么要使用激活函数?
如果没有relu等激活函数(也叫非线性),Dense层将只包含两个线性运算——点积和加法:
output = dot (W, input) + b 这样 Dense 层就只能学习输入数据的线性变换(仿射变换):该层的假设空间是从输入数据到16位空间所有可能的线性变换合集。这种假设空间非常有限,无法利用多个表示层的优势,因为多个线性层堆叠试下仍是线性运算,添加层数并不会扩展假设空间。
为了得到更丰富的假设空间,从而充分利用多层表示的优势,你需要添加非线性或激活函数。relu是深度学习中最常用的激活函数,但还是有许多其他函数可选,比如prelu、elu等。
选择损失函数和优化器。因为这个问题是二分类问题,网络输出是一个概率值(网络左后一层使用 sigmoid激活函数,仅包含一个单元),那么最好使用 binary_crossentropy(二元交叉熵)损失。这并不是唯一可行的,还可以使用 mean_squared_error(均方误差)
但对于输出概率值的模型,交叉熵(crossentropy)往往是最好的选择。交叉熵是来自于信息论领域的概念,用于衡量概率分布之间的距离,在这个例子中就是真实分布与预测值之间的距离。
下面的步骤使用 rmsprop 优化器和 binary_crossentropy 损失函数来配置模型。注意,此时我们还在训练过程中监控精度。
# 编译模型
model.compile(optimizer='rmsprop', loss='binary_crossentropy', metrics=['accuracy'])
上述代码将优化器、损失函数和指标作为字符串传入,是因为 rmsprop、binary_crossentropy 和 accuracy 都是 Keras 内置的一部分。如果你希望配置自定义优化器的参数,可通过向 optimizer 参数传入一个优化器类实例来实现:
# 配置优化器
from keras import optimizers
model.compile(optimizer=optimizers.RMSprop(1r=0.001), loss='binary_crossentropy', metrics=['accuracy'])
如果想传入自定义的损失函数或指标函数,可通过向 loss 和 metrics 参数传入函数对象来实现:
# 使用自定义的损失和指标
from keras import losses
from keras import metrics
model.compile(optimizer=optimizers.RMSprop(1r=0.001),
loss=losses.binary_crossentropy,
metrics=[metrics.binary_accuracy])
验证方法
为了验证在训练过程中监控模型在前所未见的数据上的精度,你需要将原始训练数据流出10000个样本作为验证集
# 留出验证集
x_val = x_train[:10000]
partial_x_train = x_train[10000:]
y_val = y_traain[:10000]
partial_y_train = y_train[10000:]
现在使用512个样本小组组成的小批量,将模型训练20个轮次(即对 x_train 和 y_train 两个张量中所有样本进行20次迭代)。与此同时,你还要监控在留出的 10000 个样本上的损失和精度。你可以通过将验证数据传入 validation_data 参数来完成。
# 训练模型
model.compile(optimizer='rmsprop',
loss='binary_crossentropy',
metrics=['acc'])
history = model.fit(partial_x_train,
partial_y_train,
epochs=20,
batch_size=512,
validation_data=(x_val, y_val))
在CPU上运行,每轮的时间不到2秒,训练过程将在20秒内结束。每轮结束时会有短暂的停顿,因为模型要计算在验证集的10000个样本上的损失和精度。
注意,调用 model.fit( )返回了一个History对象。这个对象有一个成员history,他是一个字典,包含训练过程中的所有数据。
>>>history_dict = history.history
>>>history_dict.keys()
dict_keys(['loss', 'acc', 'val_loss', 'val_acc'])
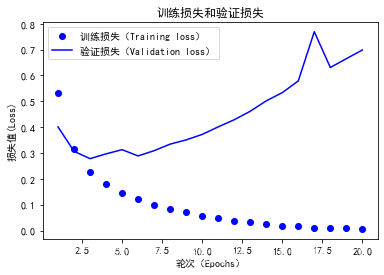
字典中包含4个条目,对于训练过程和验证过程中监控的指标。我们使用Matplotlib在同一张图上绘制训练损失和验证损失。
# 绘制训练损失和验证损失
import matplotlib as plt
history_dict = history.history
loss_values = history_dict['loss']
val_loss_values = history_dict['val_loss']
epochs = range(1, len(loss_values) + 1)
plt.plot(epochs, loss_values, 'bo', label='训练损失(Training loss)')
plt.plot(epochs, val_loss_values, 'b', label='损失验证(Validation loss)')
plt.title('训练损失和验证损失')
plt.xlabel('轮次(Epochs)')
plt.ylabel('损失值(Loss)')
plt.legend()
plt.show()
绘制训练精度和验证精度
# 绘制训练精度和验证精度
plt.clf()
acc = history_dict['acc']
val_acc = history_dict['val_acc']
plt.plot(epochs, acc, 'bo', label='训练精度(Training acc)')
plt.plot(epochs, val_acc, 'b', label='验证精度(Validation acc)')
plt.title("训练精度和验证精度")
plt.title('训练损失和验证损失')
plt.xlabel('轮次(Epochs)')
plt.ylabel('精度(Accuracy)')
plt.legend()
plt.show()
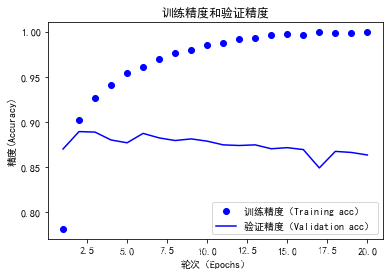
**训练损失每轮都在降低,训练精度每轮都在提升。**这就是梯度下降优化的预期结果——想要最小化的量随着每次迭代越来越小。
但是验证损失和验证精度并非如此:它们似乎在第四轮达到最佳值。
模型在训练数据上的表现越来越好,但在前所未见的数据上不一定越来越好。也就是过拟合。
在这种情况下为了放置过拟合,你可以在第三轮之后停止训练。重新训练一个新网络,训练四轮,然后在测试数据上评估模型。
model = models.Sequential()
model.add(layers.Dense(16, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(16, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))
model.compile(optimizer='rmsprop',
loss='binary_crossentropy',
metrics=['accuracy'])
model.fit(x_train, y_train, epochs=4, batch_size=512)
results = model.evaluate(x_test, y_test)
结果如下:
>>> results
[0.29863303899765015, 0.8819199800491333]
使用训练好的网络在新数据上生成预测结果
可以使用predict方法来得到评论为正面的可能大小
>>>model.predict(x_test)
array([[0.23764628],
[0.99993277],
[0.95818925],
...,
[0.13834321],
[0.08768818],
[0.71366906]], dtype=float32)
网络对某些样本的结果非常确信(大于等于0.99,或小于等于0.01),但对其他结果却不那么确信。
总结
- 通常需要对原始数据进行大量预处理,以便将其转换为张量输入到神经网络中。单词序列可以编码为二进制向量。
- 带有 relu 激活的 Dense 层堆叠,可以解决很多问题(包括情感分类)。
- 对于二分类问题,网路的最后一层应该是只有一个单元并使用 sigmoid 激活的 Dense层,网络输出应该是 0~1 范围内的标量,表示概率值。
- 对于二分类问题的 sigmoid 标量输出,使用 binary_crossentropy 损失函数。
- 无论什么问题都可以使用 rmsprop 优化器。
),但对其他结果却不那么确信。
总结
- 通常需要对原始数据进行大量预处理,以便将其转换为张量输入到神经网络中。单词序列可以编码为二进制向量。
- 带有 relu 激活的 Dense 层堆叠,可以解决很多问题(包括情感分类)。
- 对于二分类问题,网路的最后一层应该是只有一个单元并使用 sigmoid 激活的 Dense层,网络输出应该是 0~1 范围内的标量,表示概率值。
- 对于二分类问题的 sigmoid 标量输出,使用 binary_crossentropy 损失函数。
- 无论什么问题都可以使用 rmsprop 优化器。
- 随着神经网络在训练数据的表现越来越好,模型最终会过拟合,并在前所未见的数据上得到越来越差的结果。一定要一致监控模型在训练集之外的数据上的性能。
边栏推荐
猜你喜欢
随机推荐
Have bosses know date field flinksql is synchronized to the use of the null on how to deal with
path development介绍
ESP8266-Arduino编程实例-LED点阵驱动(基于Max7219)
瑞鹄转债上市价格预测
MySQL【约束】
计网试卷概念
让环境自己说话,论环境自描述的重要性
肖sir__面试接口测试
js的组成及js样式
leetcode刷题学习之路
GD32学习笔记(3)NAND Flash管理
多线程使用哈希表
再讲Promise
EssilorLuxottica借助Boomi的智能集成平台实现订单处理的现代化
shell之条件语句(条件测试、if语句,case语句)
积分商城可设置的四种兑换商品类型
【 original 】 Auto. Js the get and post case
mysql bool盲注
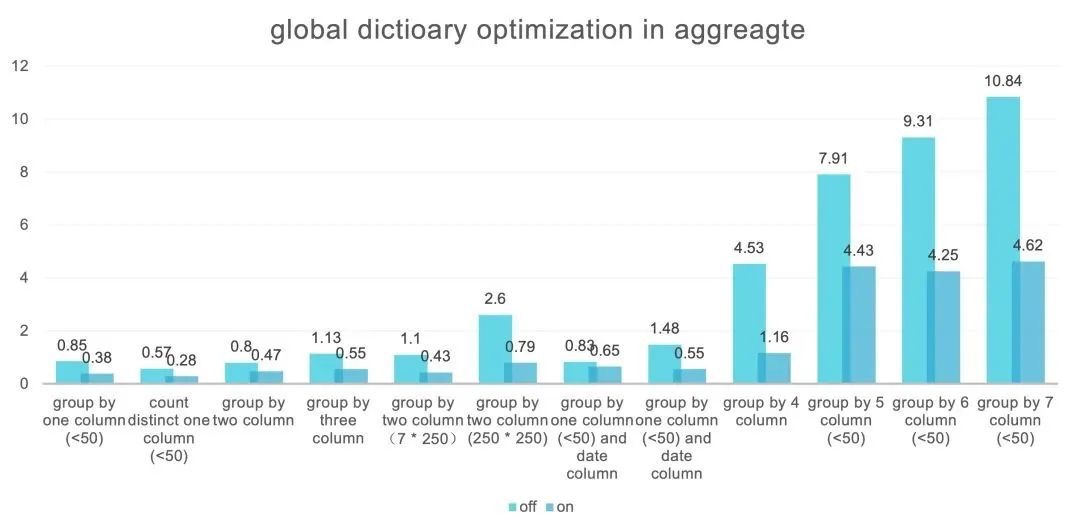
直播|StarRocks 技术内幕 :低基数全局字典优化
ESP8266-Arduino编程实例-MCP3008-ADC转换器驱动